Hello,

I am new using sMath Studio so this is likely to be something I am doing wrong but I haven't been able to make sense out of it so I'll just report it.

rpm is defined as pi/30 (1/s) . That is what it shows when I hover over a variable defined with that unit.
However, according to wikipedia and my common sense, rpm = 1/60 (1/s or Hz) = 2*pi/60 (rad/s) = pi/30 (rad/s)

That means that every time I use rpm the result is off by 2*pi which is quite annoying.


Wikipedia: https://en.wikipedia.org/wiki/Revolutions_per_minute


Regards,

SMath defines rpm as 2*pi/(60 s), where 2pi is whole angle in radians, 60s = 1 minute => the dimensions are rad/s

I know that sMath defines rpm as 2*pi/60 Hz. My point is that I think that is wrong. The wikipedia article that I shared explains it.

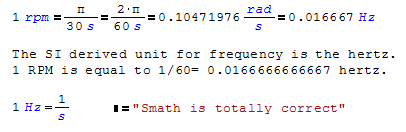
From very basics: 1 rpm = 1 rev/min = (1 rev * 1 min)/(1 min * 60 sec) = 1 rev/(60 sec) = (1/60) Hz

1 rev/sec is the definition of Hertz (https://en.wikipedia.org/wiki/Cycle_per_second)

I agree with you Javier. I had a similar problem with Mathcad ages ago.

Cycles and Herz were originally used with sinusoidal signals, hence the factor of 2*pi, but time has moved on. The SI definition of Hz is 1/s, so perhaps it is better to think of it as "events" per second (using rev in your post could be confusing because it reintroduces the notion of rotation, and hence 2*pi).
Ref: https://en.wikipedia.org/wiki/International_System_of_Units

Anyone else have a view on this?

Brian

Frequency is counts per time, no matter of what you count.
Angular frequency or angular velocity is angle per time.

They are distinct physical quantities and it is ok to expect a factor to appear if you want to transform one into the other.

The attachment is from the (partly outdated) interactive handbook, available via extension manager.

Section units angle.sm (12 КиБ) скачан 74 раз(а).

Actually, the rpm is not frequency, but angular velocity. They are not events per time unit, but amount of rotation per time unit. Notion of events is dimensionless, and events per time is (1/T) that is T^-1. Amount of rotation (angle) is dimensionless (actually, L/L), so angle per second also has dimension of ((L/L)/T) = T^-1. But their physical meaning is different, hence the factor that is required when you move from "events" to "radians".

Wrote

Anyone else have a view on this?

You have the best answer from Mike. rpm is a yardstick of "events".
View the point moving on the unit circle, one rotation is worth 2pi rad.
60 rpm = [60*2pi rad]/mn

Please, I refer again to the wikipedia article and the unit analysis I did before.

1 rpm = 1 rev/min = 1/60 rev/sec = 1/60 Hz

There is no 2*pi factor there. You need it to go to rad/sec or rad/min.

I quote from Wikipedia "Revolutions per minute (abbreviated rpm, RPM, rev/min, r/min) is a measure of the frequency of rotation, specifically the number of rotations around a fixed axis in one minute"

So I would say that yes, rpm is a measure of frequency of rotation not angular velocity. To get angular velocity then you need the 2*pi factor.

Wrote

1 rpm = 1 rev/min = 1/60 rev/sec

And it is exactly how it is defined in SMath



But 1 revolution is equal to 360° (2pi)



If you don't need relationships with the angles (the 2pi factor), simply redefine rpm

Wrote

"Revolutions per minute (abbreviated rpm, RPM, rev/min, r/min) is a measure of the frequency of rotation, specifically the number of rotations around a fixed axis in one minute"

Can't be better defined. You are confused by the word "frequency".
The frequency of something occuring per unit of time, length ...
is the number of times it happens. If in a 100 km run you drop
10 times, the frequency of dropping is 1/10 km.

Wrote

Please, I refer again to the wikipedia article and the unit analysis I did before.

1 rpm = 1 rev/min = 1/60 rev/sec = 1/60 Hz

There is no 2*pi factor there. You need it to go to rad/sec or rad/min.

I quote from Wikipedia "Revolutions per minute (abbreviated rpm, RPM, rev/min, r/min) is a measure of the frequency of rotation, specifically the number of rotations around a fixed axis in one minute"

So I would say that yes, rpm is a measure of frequency of rotation not angular velocity. To get angular velocity then you need the 2*pi factor.

You refer to Wikipedia as a definitive source of information for a non-standard unit of what? You are trying to declare (based on vague language of cited article) that rpm is a measure of frequency. If so, then you should be right.

But is that so? The Wikipedia uses some terms: "measure of the frequency of rotation", "It is used as a measure of rotational speed of a mechanical component", "Here the sign ↔ (correspondent) is used instead of = (equal)" etc. It never uses "=" where you are trying to use it.

You are writing: "1 rpm = 1 rev/min = 1/60 rev/sec = 1/60 Hz". Great!
But I write: "1 rpm = 1 rev/min = 1/60 rev/sec = (2*pi/60) rad/sec". Disprove this! Even Wikipedia doesn't disagree (see second relation in "International System of Units" section of the article). It's just that you (and I) use "=" instead of more soft "↔".

So, provided that rpm is not just "frequency", but a measure of rotational speed, that by definition is angle per time, it is defined so, to be useful in calculations and comparisons of rotational speeds expressed in different units. To convert to frequency, you need to understand the relations, and apply required transformation.

If you will find a proof that it's incorrect to treat rpm as rotational speed, then please post its source here.

Btw, you don't provide an example of an expression where "every time you use rpm the result is off by 2*pi which is quite annoying".

I don't refer to Wikipedia as a definitive source, it just derives as well naturally from the units analysis, which by the way, the one you did is correct!

I completely agree:
1 rpm = 1 rev/min = 1/60 rev/sec = (2*pi/60) rad/sec


but, that is not how sMath Studio treats it. Because according to sMath Studio: 1 rpm = (2*pi/60) Hz!!! (not rad/sec)

I know radians are unitless, but that doesn't mean that you can say rad/sec = Hz, because Hz = 1/sec, if you want to get to rad/sec you need the 2*pi factor.

An example:
I write in sMath Studio: x:=1000 rpm
then I ask it to write it in Hz, and it comes back with x = 104.7198 Hz, which I think is not right, the answer should be 1000/60= 16.6667 Hz

Moreover, I can define x:= 1000 radpm
then I ask it to write it in Hz, and it comes back with x = 16.667 Hz.

So I think that the factors are being applied the other way around.

The key here is how we define Hertz! and as far as I know, Hertz = 1/sec and not 2*pi/sec

I think we all agree in what you said: 1 rpm = 1 rev/min = 1/60 rev/sec = (2*pi/60) rad/sec

now the question is how do we get from there to Hertz?
In my opinion it should be: 1 rpm = 1 rev/min = 1/60 rev/sec = (2*pi/60) rad/sec = 1/60 Hz (not (2*pi/60) Hz)

In North America, the grid is 60 complete cycles/sec
so: the frequency is 60 Hz. In Europe you are at 50 Hz.
Also: 2*π*60 rad/sec
My 3 phases motors [normal poles] rotate 3600 rpm.

You are doing the same mistake again and again.
You write:

Wrote

I completely agree:
1 rpm = 1 rev/min = 1/60 rev/sec = (2*pi/60) rad/sec

As soon as you write that, you proclaim that rpm is measure of angular velocity. Please take a note of this fact!
Then, you write:

Wrote

but, that is not how sMath Studio treats it. Because according to sMath Studio: 1 rpm = (2*pi/60) Hz!!! (not rad/sec)

And now it becomes evident that you confuse the two distinct, incomparable physical qualities: frequency and angular velocity. And you do it on the basis that their units are the same [s^-1].

I'll try to explain this.
There are different qualities in physics, that are related, though incomparable. First, let's consider mass and energy. Take the simple relation: e=mc^2. Given that, you may tell that mass of 1 kg relates to (in a sense, is the same as) 89875.5179 TJ. But it's incorrect to write calculations, based on previous "analisys", like that, like this: x*kg+y*J=?
This kind of error is evident, and is easily caught by SMath, if you use its units feature. But if you don't, or if a software doesn't support the units concept, then this kind of problem may happen in some areas.

Let's look at another, more difficult example. In humid air properties, there exist "Mixture specific heat per unit humid air" (Cha) and "Mixture specific heat per unit dry air" (C). Both have units [J/kg/K], but the first is actually [J/kg humid air/K], and the second is [J/kg dry air/K]. If a human does not pay due attention to that, one may write something like C_1+Cha_2=? and get an erroneous result, where a software won't help catch the logical error. The same applies to specific volumes of gas (specific volume at normal conditions vs specific volume at given condition), etc.

Here we have another case of related, though very different qualities. You CANNOT measure angular velocities in Hz! Never. Hz measures frequencies. And you cannot measure frequencies in rad/s. Although they both have dimensions [T^-1].
A frequency is measure of how often some recurring event happens. Angular velocity measures how fast an angle measured from a point to another point changes WRT some chosen direction. Well, if the angular velocity is measured for a rotational movement of an object, then we also may measure its frequency - how often a point of the object will return to a chosen position. So, in this specific case, the two qualities of the rotating object relate to one another. But they are not the same!

rpm in SMath is a measure of angular velocity. Its base unit is 1 rad/s, because in SMath, 1 rad = 1. It's not 1 Hz. It's unfortunate that SMath doesn't keep that "rad" in the unit, but it just follows the SI concept to the letter.

Wrote

now the question is how do we get from there to Hertz?
In my opinion it should be: 1 rpm = 1 rev/min = 1/60 rev/sec = (2*pi/60) rad/sec = 1/60 Hz (not (2*pi/60) Hz)

Here is the answer:
AngVel := n*rpm
Freq := AngVel / 'rev
It means, to get frequency of a rotational movement, you take its angular velocity and divide by full rotation angle. That's it.

ok. I think we are getting somewhere.

I think that the root of the problem is that rpm is not an SI unit. Therefore you can consider it to be either a unit of frequency (of rotation) or a unit of angular speed.

If you consider it to be a unit of frequency (angular frequency) then 1 rpm = 1/60 Hz follows immediately. If not then you get the 2*pi factor (what sMath Studio does).

I have been looking for some information online and in most of the webpages I found they consider it to be a unit of frequency. Which makes sense to me since frequency is event for unit of time and rpm is revolution (event) for unit of time (minute).

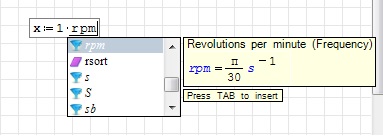
By the way, even sMath Studio (once you hover over the unit) displays it as a frequency (not angular velocity).

Wrote

By the way, even sMath Studio (once you hover over the unit) displays it as a frequency (not angular velocity).

Good point indeed. This should be changed. It also applies to some other units. This can be seen best in the insert unit dialog. There, some categories are missing:

angular velocity
angle

The angular units currently are categorized as dimensionless.

Filed as SS 2395

To deplease previous comments, Smath is totally correct
in this thread. It just happened that some i... at the
SI system decided not to count rpm on fingers but on
fractional fingers. End of it, Smath OK !