1 страниц (9 вхождений)
Single pendulum with elastic spring (k) and friction (f) - Why I have an error (???) - Сообщения
Отредактировано 01.11.2025 03:15:46
Hi. With a spring pendulum you have 2 degrees of freedom, thus you need two generalized coords. Using this post: https://smath.com/en-US/forum/topic/AeeMSM/Using-differentials:

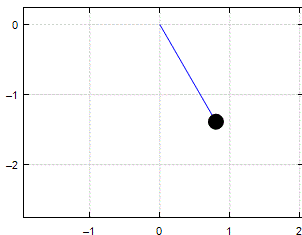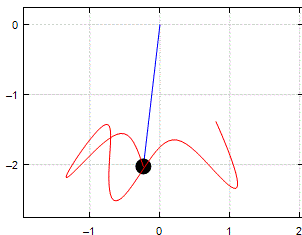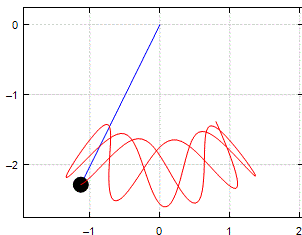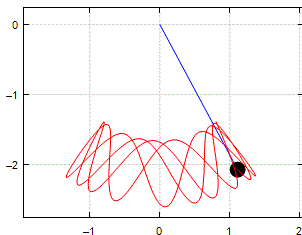
Spring_Pendulum_lagrangian.sm (120,05 КиБ) скачан 426 раз(а).
Best regards.
Alvaro.



Spring_Pendulum_lagrangian.sm (120,05 КиБ) скачан 426 раз(а).
Best regards.
Alvaro.
1 пользователям понравился этот пост
Valery Ochkov 01.11.2025 07:22:30
Is it not correct?
We have 2 degrees of freedom, but can use only one!
Pend-1-Hook.sm (16,68 КиБ) скачан 404 раз(а).
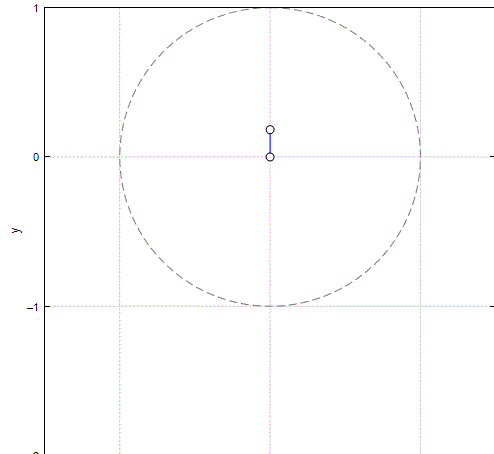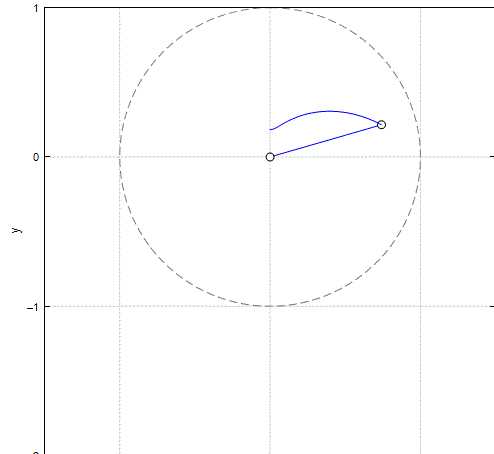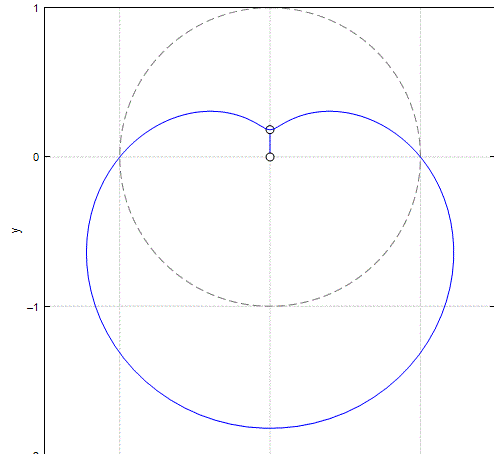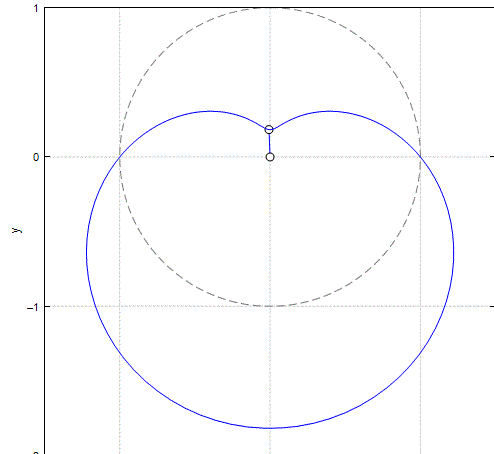
We have 2 degrees of freedom, but can use only one!
Pend-1-Hook.sm (16,68 КиБ) скачан 404 раз(а).

Отредактировано 01.11.2025 08:38:01
WroteIs it not correct?
It isn't. You can not determine the variable length only with the angle. You need another differential equation for the length. For example, see https://www.maplesoft.com/applications/Preview.aspx?id=4897

with this result:
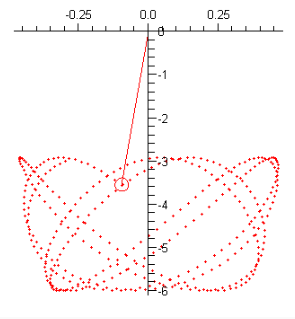
The Viacheslav's ode solver It can't handle those types of equations with that degree of coupling yet. For that, you should use the dsol I created, which should be somewhere in the forum, or use al_nleqsolve within the D function as in the other examples, or some other technique for decoupling the system.
In this case, the Lagrangian is uncoupled, so it can be solved directly.
Also, remember that the total energy is the Hamiltonian, so this is probably the correct method for solving problems when the Lagrangian is coupled.
Best regards.
Alvaro.
1 пользователям понравился этот пост
Valery Ochkov 01.11.2025 10:47:16
WroteI do not stretch or compress the spring before starting.
My case is one partical case of moution. Correct?
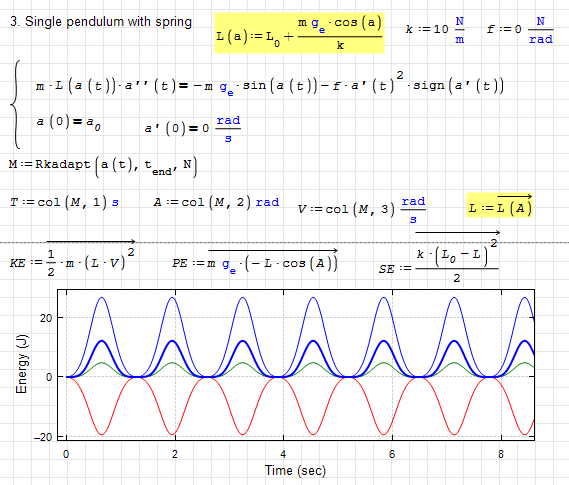
From your first file. In this example, you know the time law of Longitude, as in the first Maple example. While specifically here it's stationary (it doesn't depend directly on time, but on the angle, which does depend on time), the result is the same: you introduce a constraint, so the system's degrees of freedom are 1 instead of 2. This constraint on motion is imposed by an external force, which causes energy to flow into and out of the system, making the system's energy variable, which I understand is the original question.
However, for the system to be realistic, you need a way to control the length of the bar so that it shortens or lengthens according to the angle it forms with the vertical, which, by the way, is perfectly possible. But that system is precisely what will be modifying the total energy of the system.
Best regards.
Alvaro.
Отредактировано 01.11.2025 15:48:43
1 пользователям понравился этот пост
Valery Ochkov 01.11.2025 17:57:58
Hi. Using the RKA file ( https://smath.com/en-US/files/Download/dZeevW/RKA.sm ) from https://smath.com/en-US/forum/topic/QWpkkQ/Mathcad-Toolbox both methods (Newton and Lagrange) for the spring pendulum. The code in RKA is, like the other one, just only in SMath, this is, it does not use maple nor maxima.
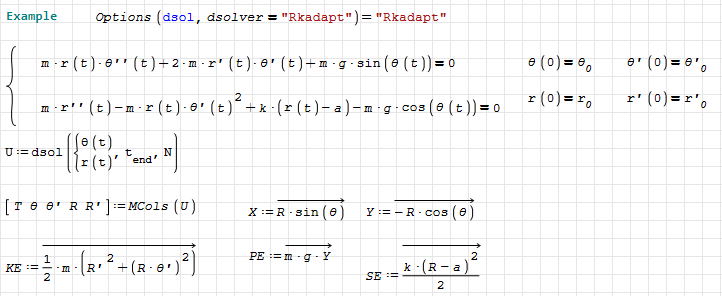
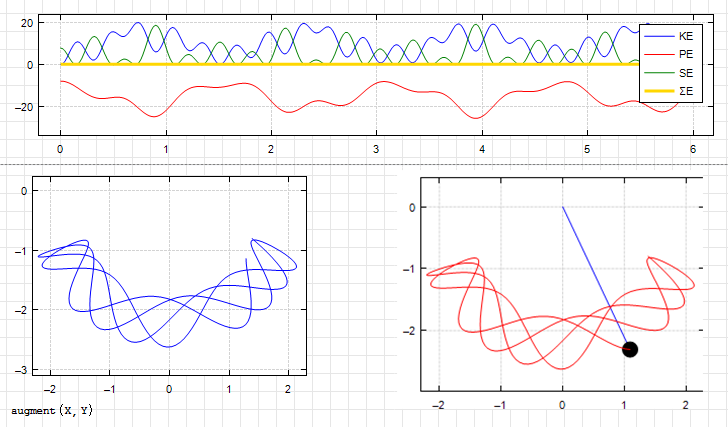
Spring_Pendulum_lagrangian.pdf (395,32 КиБ) скачан 191 раз(а).
Spring_Pendulum_lagrangian.sm (271,1 КиБ) скачан 439 раз(а).
Best regards.
Alvaro.
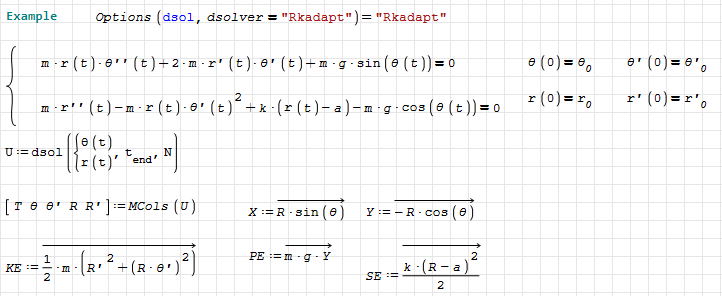

Spring_Pendulum_lagrangian.pdf (395,32 КиБ) скачан 191 раз(а).
Spring_Pendulum_lagrangian.sm (271,1 КиБ) скачан 439 раз(а).
Best regards.
Alvaro.
Отредактировано 01.11.2025 19:21:12
1 пользователям понравился этот пост
Valery Ochkov 04.11.2025 10:25:21
Hi. Friction added, Newton and Lagrange parametrized methods.
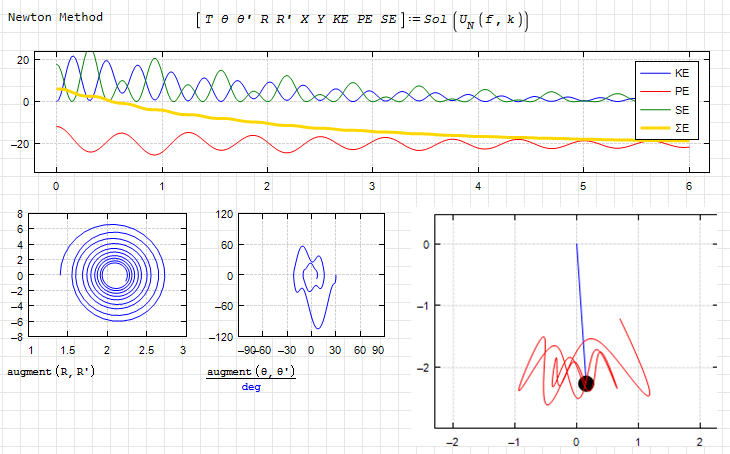
Spring_Pendulum_with_friction.sm (275,88 КиБ) скачан 442 раз(а).
Best regards.
Alvaro.

Spring_Pendulum_with_friction.sm (275,88 КиБ) скачан 442 раз(а).
Best regards.
Alvaro.
1 пользователям понравился этот пост
sergio 02.11.2025 16:40:15
1 страниц (9 вхождений)
- Новые сообщения
- Нет новых сообщений