1 страниц (15 вхождений)
Bilinear interpolation - Сообщения
Hello,
could you please suggest an efficient bilinear interpolation algorithm?
Now I use this rather ugly ang inefficient function, that will take forever (see attachment).
To make this more efficient, I must look for two adjacent columns and two adjacent rows, taking into account possible unsorted input, possibly outside position (extrapolation) and possible perfect match. This will likely be slow, too. Maybe there's any better approach?
Thank you.
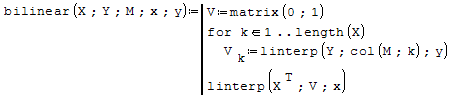
could you please suggest an efficient bilinear interpolation algorithm?
Now I use this rather ugly ang inefficient function, that will take forever (see attachment).
To make this more efficient, I must look for two adjacent columns and two adjacent rows, taking into account possible unsorted input, possibly outside position (extrapolation) and possible perfect match. This will likely be slow, too. Maybe there's any better approach?
Thank you.
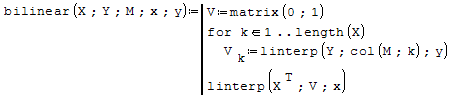
С уважением,
Михаил Каганский
1 пользователям понравился этот пост
Davide Carpi 17.02.2014 18:23:00
Thanks, Ioan,
the matrix(0,1) thing here is for those cases when V happens to be defined outside, thus being non-local variable. So here we effectively clear it (and ensure proper matrix type and dimension, while being empty). Otherwise, this may give unexpected results (if V is vector with more than length(X) rows), or errors (if V is not an array).
Other solution (though not bullet-proof) would be using some very strange and hardly-reusable name (like bilinear_local_V).
Yet another (and preferrable) would be a means to define V as local-only variable...
I'll try to compare the performance of the functions ASAP.
the matrix(0,1) thing here is for those cases when V happens to be defined outside, thus being non-local variable. So here we effectively clear it (and ensure proper matrix type and dimension, while being empty). Otherwise, this may give unexpected results (if V is vector with more than length(X) rows), or errors (if V is not an array).
Other solution (though not bullet-proof) would be using some very strange and hardly-reusable name (like bilinear_local_V).
Yet another (and preferrable) would be a means to define V as local-only variable...
I'll try to compare the performance of the functions ASAP.
С уважением,
Михаил Каганский
1 пользователям понравился этот пост
ioan92 20.02.2014 17:15:00
Here is a typical result on my computer (using your sample data). The results are consistently reproducible (±0.010s)
Notably slower is (surprisingly) Inter2dd, while Inter2d is steadily faster (though not that much faster - I suppose that further optimisation could give greater boost) than my variant. I wonder why these two almost identical functions work so differently in terms of performance?
I didn't test for corner cases yet. Also, larger tables should be tested as well.

Notably slower is (surprisingly) Inter2dd, while Inter2d is steadily faster (though not that much faster - I suppose that further optimisation could give greater boost) than my variant. I wonder why these two almost identical functions work so differently in terms of performance?
I didn't test for corner cases yet. Also, larger tables should be tested as well.

С уважением,
Михаил Каганский
1 пользователям понравился этот пост
ioan92 21.02.2014 05:02:00
As for me the fastest is bilinearid followed by Inter2dd...
Sometimes seems to me that performances are also affected by the position... if I place my InterBil on top or on the bottom of the list below I can see an high difference...
interpol2f.sm (75,61 КиБ) скачан 949 раз(а).
Sometimes seems to me that performances are also affected by the position... if I place my InterBil on top or on the bottom of the list below I can see an high difference...
interpol2f.sm (75,61 КиБ) скачан 949 раз(а).
If you like my plugins please consider to support the program buying a license; for personal contributions to me: paypal.me/dcprojects
1 пользователям понравился этот пост
ioan92 21.02.2014 05:02:00
Thank you w3b5urf3r_reloaded,
here at home, I see the same results as you do. Seems that this is something machine-dependent...
Your "Limits" almost literally repeats "k1" by ioan92, but doesn't allow for backwards-sorted input, and for unclear reason restricts extrapolation. k1 is faster (partly because eval in "Limits" seem to slow it down a bit), and may be made yet (marginally) faster if the innermost loop is started from k:=2 instead of k:=1.
All the functions use different arguments passing order. I must say that I chose the original order to closely follow the *interp() family in smath. Well, except swapping rows and columns
Still, Inter2d is the fastest (on the computer I use at the moment) when used against a real matrix (23x13), with 6x speed gain over my bilinear.
The only "weakness" of it is that it cannot handle "unsorted" input, which should be extinctly rare. I suppose it's my choice. Thank you ioan92!
bilinear-final.sm (10,04 КиБ) скачан 977 раз(а).
here at home, I see the same results as you do. Seems that this is something machine-dependent...
Your "Limits" almost literally repeats "k1" by ioan92, but doesn't allow for backwards-sorted input, and for unclear reason restricts extrapolation. k1 is faster (partly because eval in "Limits" seem to slow it down a bit), and may be made yet (marginally) faster if the innermost loop is started from k:=2 instead of k:=1.
All the functions use different arguments passing order. I must say that I chose the original order to closely follow the *interp() family in smath. Well, except swapping rows and columns
Still, Inter2d is the fastest (on the computer I use at the moment) when used against a real matrix (23x13), with 6x speed gain over my bilinear.
The only "weakness" of it is that it cannot handle "unsorted" input, which should be extinctly rare. I suppose it's my choice. Thank you ioan92!
bilinear-final.sm (10,04 КиБ) скачан 977 раз(а).
С уважением,
Михаил Каганский
2 пользователям понравился этот пост
Thank you Mike 
this is because the function was taken and updated from an old worksheet where extrapolation had not physical sense
You might try to take a look here and here
Wroteand for unclear reason restricts extrapolation.
this is because the function was taken and updated from an old worksheet where extrapolation had not physical sense
WroteMy obsession is on how to improve indices position finding function - k1; one idea is to look the x/x0 ratio, in respect with 1; significant situations parameters are ascending / descending order of vectors, interpolation / extrapolation; x, y vectors monotony is a condition also.
You might try to take a look here and here
If you like my plugins please consider to support the program buying a license; for personal contributions to me: paypal.me/dcprojects
1 пользователям понравился этот пост
ioan92 21.02.2014 07:26:00
For index finding one might use the boolean matrix functions from uni's Matlab c++ plugin.
mwlt returns an array with 1 everywhere the entries in the argument matrix are less than a given value. Then, finding the index is reduced to summing up the ones.
However, I cannot demonstrate that in 0.97 as the plugin does not seem to work. Functions are undefined although the plugin is installed and should in principle not be affected by the API changes.
EDIT: with 0.96.4909 (inofficial portable version) the matlab plugin works. However, matlab should have a lookup function, didn't check that.
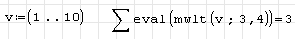
mwlt returns an array with 1 everywhere the entries in the argument matrix are less than a given value. Then, finding the index is reduced to summing up the ones.
However, I cannot demonstrate that in 0.97 as the plugin does not seem to work. Functions are undefined although the plugin is installed and should in principle not be affected by the API changes.
EDIT: with 0.96.4909 (inofficial portable version) the matlab plugin works. However, matlab should have a lookup function, didn't check that.
Technische Mechanik mit SMath Studio: https://link.springer.com/book/10.1007/978-3-658-50592-9
2 пользователям понравился этот пост
yet another index function:
[MATH lang=ENG]index(YY,y):line(j:0,while(el(YY,j+1)
[MATH lang=ENG]index(YY,y):line(j:0,while(el(YY,j+1)
Technische Mechanik mit SMath Studio: https://link.springer.com/book/10.1007/978-3-658-50592-9
1 пользователям понравился этот пост
ioan92 22.02.2014 03:00:00
I've added a rude implementation of the Ioan "bilinear-final i" solution in my custom functions plugin... seems quite fast, someone can test it?
function: InterpBilinear(row X,column Y,matrix M,number x,number y)
BTW to improve the margin() performances on large matrices, if we assume that the X and Y vectors are both sorted, a way could be to use a "divide and conquer" algorithm (basically, a bisection through the vectors indices)
function: InterpBilinear(row X,column Y,matrix M,number x,number y)
BTW to improve the margin() performances on large matrices, if we assume that the X and Y vectors are both sorted, a way could be to use a "divide and conquer" algorithm (basically, a bisection through the vectors indices)
If you like my plugins please consider to support the program buying a license; for personal contributions to me: paypal.me/dcprojects
2 пользователям понравился этот пост
Thank you all! 
Actually, this function is used at most two times, at least zero times. If the function is executed on an evenly distributed data, it will be absolutely no difference in my and your variants: my zero invocations when extrapolating left will be compensated by two invocations when extrapolating right, and when interpolating, exactly one invocation will be anyway. In your variant, it will always be invoked exactly once (or maybe it should be eval'ed for this?). So, your variant will win on data that tends to right, while mine will do better on data shifted to the left.
Well, while eval() in index function seems to slow things down, this specific eval() proves to speed thing up (I must confess that not that much, though). Attached is your file with my speed test. When two functions are compared side-by-side in series of 3150+ invocations, doing 40 tests, the resulting numbers show on my computer: 3150 invocations of my function are faster than equal count of the modified one by ~0.14 s. The data I used for testing is left-shifted, so I also used your variant without length() optimization, then testing my function is still faster by ~0.09 s (~3%). It's up to implementer to decide if this worth it. I only describe it because I need to maximize speed by all means.
Well, I seem to make things cumbersome.
In my initial version, it was convenient (to me) to specify column first, then row. This matched the underlying formula order, so I used it.
Then I sent it here without changing things, and then you corrected me in your proposals. I agreed with you, because it's a common thing to cpecify row first, then column, when working with matrices. So when posting my "final" variant, I fixed this. But I named the params X and Y (x and y respectively). And thus, it seems that I introduced another problem: using these indices, I imply then the matrix is treated as a carthesian coordinates, where X is usually horizontal coordinate, and Y is vertical one.
Excuse me for overly-complicating things. I don't know which order is "better" (more intuitive), but anyway, the naming of params surely must reflect the order: X and Y are suitable only if X is horizontal (column index), otherwise they must be Row and Col to make things clear.
Unfortunately, this one is oversimplified variant of ioan92 "k1", and this variant is incorrect (fails at extrapolating right), in addition to being not optimized for corner cases. Also, it requires about twice as much additions. I haven't tested your other proposal (I cannot use Matlab plugin), but being very elegant, I doubt it will be more efficient than ioan92's one: it will need to traverse matrices twice.
w3b5urf3r_reloaded, I'll try to test your plugin ASAP. Thank you!
bilinear-final i+test.sm (82,91 КиБ) скачан 996 раз(а).
Wrote1. length(x) is used 4 times; it's preferable to introduce it from the beginning into a variable
Actually, this function is used at most two times, at least zero times. If the function is executed on an evenly distributed data, it will be absolutely no difference in my and your variants: my zero invocations when extrapolating left will be compensated by two invocations when extrapolating right, and when interpolating, exactly one invocation will be anyway. In your variant, it will always be invoked exactly once (or maybe it should be eval'ed for this?). So, your variant will win on data that tends to right, while mine will do better on data shifted to the left.
Wrote2. eval function seems not indispensable (?)
Well, while eval() in index function seems to slow things down, this specific eval() proves to speed thing up (I must confess that not that much, though). Attached is your file with my speed test. When two functions are compared side-by-side in series of 3150+ invocations, doing 40 tests, the resulting numbers show on my computer: 3150 invocations of my function are faster than equal count of the modified one by ~0.14 s. The data I used for testing is left-shifted, so I also used your variant without length() optimization, then testing my function is still faster by ~0.09 s (~3%). It's up to implementer to decide if this worth it. I only describe it because I need to maximize speed by all means.
Wrote3. column vector is used to intercept line position in the line matrix; so the matrix indices must be transposed.
Well, I seem to make things cumbersome.
In my initial version, it was convenient (to me) to specify column first, then row. This matched the underlying formula order, so I used it.
Then I sent it here without changing things, and then you corrected me in your proposals. I agreed with you, because it's a common thing to cpecify row first, then column, when working with matrices. So when posting my "final" variant, I fixed this. But I named the params X and Y (x and y respectively). And thus, it seems that I introduced another problem: using these indices, I imply then the matrix is treated as a carthesian coordinates, where X is usually horizontal coordinate, and Y is vertical one.
Excuse me for overly-complicating things. I don't know which order is "better" (more intuitive), but anyway, the naming of params surely must reflect the order: X and Y are suitable only if X is horizontal (column index), otherwise they must be Row and Col to make things clear.
Wroteyet another index function
Unfortunately, this one is oversimplified variant of ioan92 "k1", and this variant is incorrect (fails at extrapolating right), in addition to being not optimized for corner cases. Also, it requires about twice as much additions. I haven't tested your other proposal (I cannot use Matlab plugin), but being very elegant, I doubt it will be more efficient than ioan92's one: it will need to traverse matrices twice.
w3b5urf3r_reloaded, I'll try to test your plugin ASAP. Thank you!
bilinear-final i+test.sm (82,91 КиБ) скачан 996 раз(а).
С уважением,
Михаил Каганский
2 пользователям понравился этот пост
WroteI've added a rude implementation of the Ioan "bilinear-final i" solution in my custom functions plugin...
It's 3+ times faster than "bilinear-final i". Great!
Binary search could of course be used in cases where the indices are ~evenly spaced...
С уважением,
Михаил Каганский
2 пользователям понравился этот пост
Well, as I noted earlier, I don't consider first Martin's suggestion efficient enough. It's beautiful, though, but it requires two passes of length(X): first to create matrix with ones, and second to sum them up.
Ioan's last variant improves it somewhat, but it still requires one full pass. In what sense is it superior to Ioan's initial k1()? It has no double logic.
OK, as exotic variants are considered here, I post my own, that I made after Ioan suggested his initial version of k1(). It is based on Ioan's, but removes doubling of logic. It won't have to iterate through all the vector, only the first part that is less (more) than lookup value. Still, it's less efficient than final version used in my post 7, because it uses extra function call.
margin.sm (4,4 КиБ) скачан 954 раз(а).
Ioan's last variant improves it somewhat, but it still requires one full pass. In what sense is it superior to Ioan's initial k1()? It has no double logic.
OK, as exotic variants are considered here, I post my own, that I made after Ioan suggested his initial version of k1(). It is based on Ioan's, but removes doubling of logic. It won't have to iterate through all the vector, only the first part that is less (more) than lookup value. Still, it's less efficient than final version used in my post 7, because it uses extra function call.
margin.sm (4,4 КиБ) скачан 954 раз(а).
С уважением,
Михаил Каганский
2 пользователям понравился этот пост
A test through the Margin() solutions... BTW IMHO is preferable a test with less iterations but bigger matrices...
[edit 1] file updated (previously missing xx and yy values on the canvas)
[edit 2] screenshot updated using the file above
![2014-02-23 02_48_16-SMath Studio Desktop - [bilinear-final i - mod.sm_].png](/ru-RU/files/Download/unGTxr/2014-02-23-02_48_16-SMath-Studio-Desktop---[bilinear-final-i---mod.sm_].png)
[edit 1] file updated (previously missing xx and yy values on the canvas)
[edit 2] screenshot updated using the file above
![2014-02-23 02_48_16-SMath Studio Desktop - [bilinear-final i - mod.sm_].png](/ru-RU/files/Download/unGTxr/2014-02-23-02_48_16-SMath-Studio-Desktop---[bilinear-final-i---mod.sm_].png)
If you like my plugins please consider to support the program buying a license; for personal contributions to me: paypal.me/dcprojects
2 пользователям понравился этот пост
Hello Ryan,
I can confirm the bug, really dangerous o_o
Win7 x64, SMath Studio 0.97.5154 (Desktop)
Best regards,
Davide
end file.sm (1,97 КиБ) скачан 924 раз(а).
I can confirm the bug, really dangerous o_o
Win7 x64, SMath Studio 0.97.5154 (Desktop)
Best regards,
Davide
end file.sm (1,97 КиБ) скачан 924 раз(а).
If you like my plugins please consider to support the program buying a license; for personal contributions to me: paypal.me/dcprojects
1 пользователям понравился этот пост
ioan92 05.03.2014 14:10:00
I think should be moved in the bugs section, before losing it...
If you like my plugins please consider to support the program buying a license; for personal contributions to me: paypal.me/dcprojects
1 пользователям понравился этот пост
ioan92 12.03.2014 03:44:00
1 страниц (15 вхождений)
- Новые сообщения
- Нет новых сообщений
