I am having problem while evaluating specific heat capacity from given data while invoking unit calculation as well

Radovan, I do not think is correct your indication (Wrong/Right) as it is a temperature range you must use ' Δ °C.
Using the Kelvin grades instead this differentiation is not necessary (in fact in the Smath standard there is no ' Δ K).

sergio

Wrote

Radovan, I do not think is correct your indication (Wrong/Right) as it is a temperature range you must use ' Δ °C.
Using the Kelvin grades instead this differentiation is not necessary (in fact in the Smath standard there is no ' Δ K).

Hello Sergio,

This was mentioned many times and I just wanted to point out that if you have something in ' °C you have to add or subtract in ' Δ °C (and not in ' °C) to get the result in ' °C.
I agree with you. The simplest thing is just to use ' Δ °C only when the temperature difference is the case.



I should have mentioned this as well.

Regards,
Radovan

Wrote

I agree that the first line is wrong regardless what you actually want to express.

• If the two operands are really meant to be temperature points then the result is a change or difference of temperatures and it's unit must be left to K or set to Delta°C. Setting it to °C is wrong.
  
• If the second operand actually is meant to be a temperature difference or change, then it must have the unit K or Delta°C.

The second line can be right or wrong, depending on your actual intent.

• If the first operand is a meant to be a temperature point and second operand is meant to be a temperature difference or change, then the result is a temperature point and the unit can be K or °C. Nothing wrong then.
  
• Surely, if the equation is meant to represent something different, then it would be wrong. But that can be said of any equation in any document.

If everything is meant to be temperature differences, then this one is correct:

In my opinion, the correct writing is as follows:

[albumimg]1512[/albumimg]

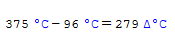
Smath does not do it independently (because it returns the result in ' K) and then if you want to act manually on the unit of measure ' Δ ° C

I would add that, indeed, for those who have not followed the numerous interventions on the forum, it is difficult to operate correctly.

sergio

The right way is @ post 4,
i.e: put unit on the maths, not on individuals

Wrote

In my opinion, the correct writing is as follows:

[albumimg]1512[/albumimg]

Smath does not do it independently (because it returns the result in ' K) and then if you want to act manually on the unit of measure ' Δ ° C

I would add that, indeed, for those who have not followed the numerous interventions on the forum, it is difficult to operate correctly.

sergio

Correct as well ...which brings us to the first post. If the question missed the point, the answer will be as well. Actually, it seems there was all right with the picture. We had many correct answers ... but, what was the question actually ???

Wrote

If the question missed the point, the answer will be as well. Actually, it seems there was all right with the picture. We had many correct answers ... but, what was the question actually ???

Quite right: wrong question may be implicit of wrong answer !
Assume you have a differential meter, it performs [a-b]and you put
the unit you wish ... per say => answer= $
SI temperature unit is K ... thus post 4 is correct two ways.

Hi. It's an old resolution, but figures in the last version: https://www.bipm.org/utils/common/pdf/si_brochure_8.pdf



The last proposed revisions warm about the temperature differences, but claim for the use of ºC (https://www.bipm.org/utils/en/pdf/si-revised-brochure/Draft-SI-Brochure-2018.pdf):



So, I don't see the place of the Delta Celsius.

Best regards.
Alvaro.

Wrote

So, I don't see the place of the Delta Celsius.

Best regards.
Alvaro.

In order to follow the rules in the document, you need to tell temperature differences from absolute (or thermodynamic) temperature for a given quantity. Thus, any object representing such quantities must have an attribute to indicate the type.

In non-automatic documents, the correct conversion between K and °C (with or without offset) is done based on context information, which is outside the actual maths.

The regulations ignore the needs of context-free self-contained physical equations handling. Just as Eurocode ignores FEA for local stresses.

Thus, whenever you want to use °C in automatic documents with unit handling, you have to indicate on a per-use base, which conversion to apply. In SMath, values of physical quantites are represented by unit and number. In some cases, the correct application of conversion rules or the correct choice of result units would require additional information (type of quantity) be taken into account.

The place of Delta°C or Delta°F is being a way to convey (and indicate) this information to the logic. I think it does the trick without blowing up the underlying infrastructure.

If you want to use °C in SMath, you most likely also have to be aware of Delta°C.

Unit tracking in SMath isn't really quantity tracking but it helps doing physical calculations correctly.

Hi

I don't know the internals but my guess is that the wrong answer is a bug. Wolfram alpha don't need a context for giving the correct results for temperature differences. And seems that smath don't store the value in K but in C. Storing internally all values in K could correct the temperature bug and make the delta C unit useless.

Best regards.
Alvaro

Wrote

Hi

I don't know the internals but my guess is that the wrong answer is a bug. Wolfram alpha don't need a context for giving the correct results for temperature differences. And seems that smath don't store the value in K but in C. Storing internally all values in K could correct the temperature bug and make the delta C unit useless.

Best regards.
Alvaro

Storing all values in K actually is the source of the problem. When values given in °C are to be stored in K, then you need to know whether you have a difference or a thermodynamic temperature. Would you prefer a context menu entry to provide that information?

There is a way to consistently use °C: use this exclusively for the whole document and all occurances of temperature quantities. All gradients, conductivities, capacities etc must use °C in their definitions as well and do no conversion to K internally. You actually can do that in SMath by defining your own °C unit, here I defined one with an attached space character:


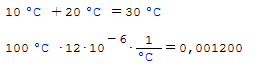
celsius.sm (2 КиБ) скачан 37 раз(а).

The drawback of this is that you can't convert such °C based quantities to K without saying if the offset is to be applied.
Edit: Also, you are restricted to the setting °C or K globally for the document and can't make the decision on a per input/output base.

Wrote

Storing all values in K actually is the source of the problem. When values given in °C are to be stored in K, then you need to know whether you have a difference or a thermodynamic temperature. Would you prefer a context menu entry to provide that information?

Oh, yes, you're wright, problem isn't not convert, is convert. But what I want to say, and can't do very well as you can see, is that ºC can't operate at the same way in the "lhs" and the "rhs" of evaluations. Maybe with this can solve the contextual problem.

This is: at left side, thus before evaluations, store as the unit for temperature differences without conversion, but for the right side, this is, only for show units, actuate as a post fix operator but not as an usual unit, even it could be with other units (and same thing for ºF). If I'm not wrong again, I guess that this gives the enough information about which context the temperature is: thermodynamics or difference temperature.

Wrote

There is a way to consistently use °C: ...

It seems a very strong, consistent and quick workaround solution for use SI standards. Thanks for this.

Wrote

...(the other stuff)

Quite right.

Wrote

Unit tracking in SMath isn't really quantity tracking but it helps doing physical calculations correctly.

This is why I say that for practical engineering calculus SMath could be a best option than Maple or Mathematica. Maybe not yet, but for sure, soon.

Best regards.
Alvaro.