1 страниц (7 вхождений)
Integral over a closed domain - Сообщения
Hi everyone,
I'm looking for some tips to make applications about the integration of a function over a closed non rectangular domain (i.e Green's theorem)
I'm looking for some tips to make applications about the integration of a function over a closed non rectangular domain (i.e Green's theorem)
Physics is like sex. Sure, it may give some practical results, but that’s not why we do it. (R. Feynman)
In short: area of a closed contour goes by the rule of the polygon.
Something in preparation ~ one day.
Not so easy on some difficult f(x,y) that have no symbolic.
Cheers ... Jean
Something in preparation ~ one day.
Not so easy on some difficult f(x,y) that have no symbolic.
Cheers ... Jean
1 пользователям понравился этот пост
SteelCat 22.05.2020 12:11:00
On a textbook I found some applications with a fictitious rettangular domain and a function (theta in the picture) defined from vertices coords, that accounts for the effective boundary.
It certainly works, but maybe there is something more elegant, even for numerical applications ...
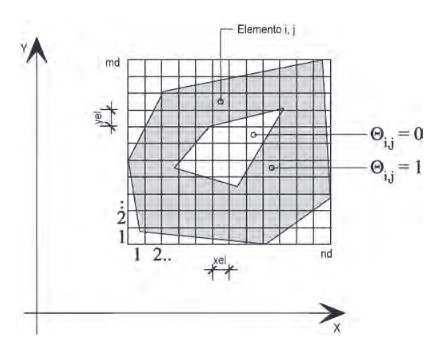
It certainly works, but maybe there is something more elegant, even for numerical applications ...

Physics is like sex. Sure, it may give some practical results, but that’s not why we do it. (R. Feynman)
That was done multiple times, recently.
Construct the polygons from the book data.
Attach the Smath document ... like done.
Cheers ... Jean
Construct the polygons from the book data.
Attach the Smath document ... like done.
Cheers ... Jean
WroteOn a textbook I found some applications with a fictitious rettangular domain and a function (theta in the picture) defined from vertices coords, that accounts for the effective boundary.
It certainly works, but maybe there is something more elegant, even for numerical applications ...
You could use finite elements. Create a mesh e.g. of triangles and use some quadrature formula inside the triangles based on some interpolation formula between the vertices (and for second order approximation also midside node). This provides an approximation which gets better with finer mesh.
So what you need is:
- A triangulation method
- an generic element integrator and
- some integration loop over all elements.
The most simple integrator for linear triangles is the average of the nodal values times the area of the triangle, but you also could use some quadrature formula based on internal locations (like Gauss quadrature).
If you have a closed form integral for a single triangle of arbitrary size, then you can create a triangulation just using the boundary points without further mesh generation. The result is exact in this case.
Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
WroteWroteOn a textbook I found some applications with a fictitious rettangular domain and a function (theta in the picture) defined from vertices coords, that accounts for the effective boundary.
It certainly works, but maybe there is something more elegant, even for numerical applications ...
You could use finite elements. Create a mesh e.g. of triangles and use some quadrature formula inside the triangles based on some interpolation formula between the vertices (and for second order approximation also midside node). This provides an approximation which gets better with finer mesh.
So what you need is:
- A triangulation method
- an generic element integrator and
- some integration loop over all elements.
The most simple integrator for linear triangles is the average of the nodal values times the area of the triangle, but you also could use some quadrature formula based on internal locations (like Gauss quadrature).
If you have a closed form integral for a single triangle of arbitrary size, then you can create a triangulation just using the boundary points without further mesh generation. The result is exact in this case.
Many thanks for your point of view.
Physics is like sex. Sure, it may give some practical results, but that’s not why we do it. (R. Feynman)
WroteIt certainly works, but maybe there is something more elegant, even for numerical applications ...
More elegant than what ?
Maths Polygon Area_Perimeter.sm (75,53 КиБ) скачан 597 раз(а).
1. Construct your 2 polygons.
2. From the big one: subtract area of small from big.
3. That tread goes no where from nothing.
1 страниц (7 вхождений)
- Новые сообщения
- Нет новых сообщений
