How to solve this in SMath - Сообщения
.gif)
I finally took a ride along this road with my granddaughter. On the way, I was not thinking about the beauty of Moscow, but about how to solve this problem at SMath.

Mathcad 15
Catenary-G-fixed.xmcd (58,54 КиБ) скачан 791 раз(а).
If anyone can solve it as in mathcad, later parts can be implemented too.
Some can solve Minimum of a single variable function with derivation of it.
I don't know how to do it with more than 1 variables as in your example.
Regards
catenary_G.sm (43,76 КиБ) скачан 831 раз(а).
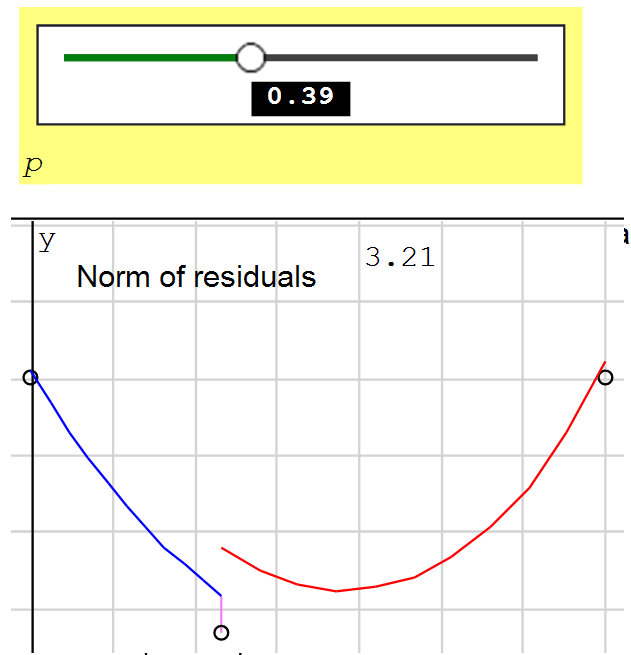
The solution is unreliable at the endpoints. The procedure is Newton-Raphson with approximated gradient.
Each new iteration uses the result of the previous one as initial guess. This is done using absolute variables. Just follow the instructions to properly initialize the procedure.
![2024-04-15 22_11_13-SMath Solver - [Seilbahn5a.sm_].png](/ru-RU/files/Download/L5bRhM/2024-04-15-22_11_13-SMath-Solver---[Seilbahn5a.sm_].png)
Seilbahn5a.sm (60,26 КиБ) скачан 814 раз(а).
I think that it could be possible to deal with the problem as a structural equilibrium one, using a FEM technique. The drawing and the animation are details after having the right results.
It seems that the rope is considered as inextensible; an approximation not always accepted.
The proposed dimensions let us think more to a sort of toy than to a technical object as that from the photo.
However, this does not represent a too high difficulty for looking for a solution. In fact, for each X given abscissa value, there is to obtain the Y ordinate value for the nacelle position. In each (X;Y) nacelle position, the force’s equilibrium must be assured. This is the way to determine the Y for each given X. The traction rope must assure the missing force to fix the nacelle in a position. Without knowing the traction rope data, the problem is not enough defined (?).
Another variable could be the length of one of the two segments of the cable...
If I understand, the proposed problem includes some input features and data as:
• A unique nacelle rolling with a pulley on the carrying rope (???) : G=10 g.
• A carrying rope : dX = 10cm; dY = 7cm; L = 15cm; gc = 5g/cm; Gc = 15cm x 5g/cm = 75g.
• A traction rope: undefined as geometry and its end support positions. (???) Its behavior is unclear for me …
An equillibrium possibility:
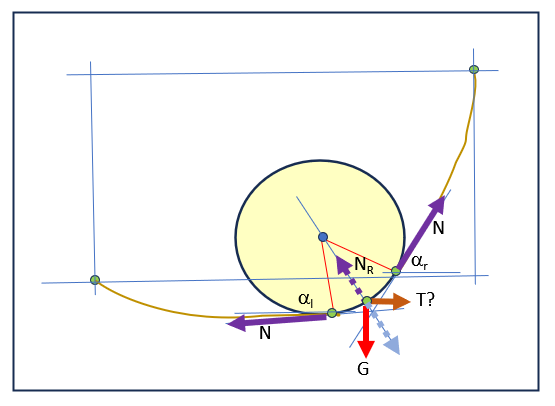
Best regards,
Ioan
I asked if the animation introduced by Valery concerns a real technical problem like in his photo or is a simple mathematical abstract discussion.
Perchance, I’m familiar enough with cable’s analysis focusing on the engineering use. Next, I’ll point some basics, as I understand them now. I’m grateful for any eventual critics or suggestions.
From the practical viewpoint, there are two main families of cable transportation application:
* Using one alone cable with the cabins sealed on it:


* Using a couple of:
i. a carrying cable, on which the cabin(s) are rolling with pulleys and
ii. another traction cable for controlling the movements of cabin(s).


From geometrical viewpoint, an inextensible catenary (cosh(x)) cable is a plan figure, enough defined by three geometrical data (e.g.: the two projections H and V and the developed length of the cable L).
From mechanical viewpoint it is necessary to know also the load (constant on the whole length of the cable) w.
These data are enough to establish its full geometry and also the 4 (3 distinct – the two horizontal reactions are equal) values of reactions on its length using one equation.
The problem in discussion here can be reduced to a couple of two elementary cables, linked to the point where the G force from the cabin is applied. For each position of the cabin fixed on the cable, there can be identified two elementary cables.
A solution to obtain the two coordinates of the cabin is (as Martin mentioned) to use as input variable the length of one of the two elementary cables and to deduct from the two equilibrium projections, the two coordinates of the cabin (X and Y). These can be used to draw (animate) the cabin’s position.
A parametric formulation is useful.
Once these hypotheses are accepted, the rest is nothing than some mathematical developments. I do not reproduce all the mathematics development here because I’m in a publishing progress with the subject of catenary and parabolic cable as well extensible as not extensible.
Best Regards,
Ioan
https://www.routledge.com/25-Problems-for-STEM-Education/Ochkov/p/book/9781032174624).
We take an inextensible cable of length L and with a known specific gravity (the mass of one meter of cable). We attach a load of known mass to this cable at a distance l from one end of the cable. Next, the cable with the load is attached at two points. It is necessary to determine the geometry of the cable sag and the force at the attachment points. Then you need to change the value of l from zero to L and create an animation.
I can do this in Mathcad, but I cannot do it in SMath. I turned to you for help.
WroteMy students solve this problem at the intersection of mathematics, mechanics and computer science (STEM education - see
https://www.routledge.com/25-Problems-for-STEM-Education/Ochkov/p/book/9781032174624).
We take an inextensible cable of length L and with a known specific gravity (the mass of one meter of cable). We attach a load of known mass to this cable at a distance l from one end of the cable. Next, the cable with the load is attached at two points. It is necessary to determine the geometry of the cable sag and the force at the attachment points. Then you need to change the value of l from zero to L and create an animation.
I can do this in Mathcad, but I cannot do it in SMath. I turned to you for help.
OK – Now, you clearly defined the problem that you and your students had solved.
My question is: do you intend to associate your solution to a really technical situation, or it is only an abstract construction "game"?
,
From my understanding – if you fix the cable at its two ends, it is not clear how do generate, physically, the mass movement?
As I mention in my post #9, for such a case, there are introduced a pulley and a second cable for traction. If you solve the technical side of the problem in a different mode, how do assure the forces equilibrium?
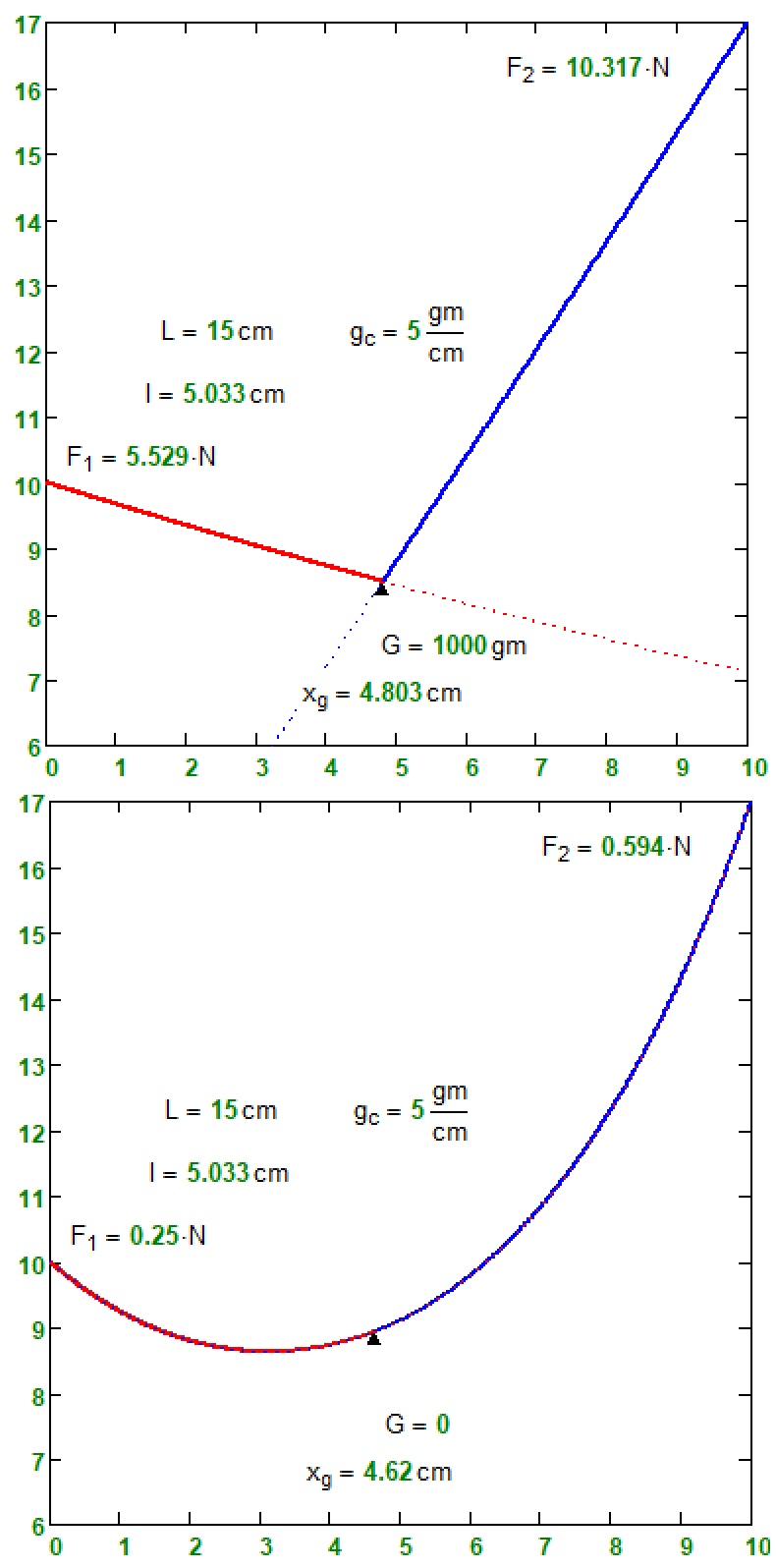
In respect with your post #1 animation, what is not clear for me is: if red and blue continue the line is the problem’s unique cable, what is the physical meaning of the second (pointed) line?
If G=0 we have one line.
WroteThe dotted lines are a phantom continuation of the catenary.
If G=0 we have one line.
If the cable is fixed on its two ends, "the phantom" must be a cosh curve passing through this 2 same points ??? !!!
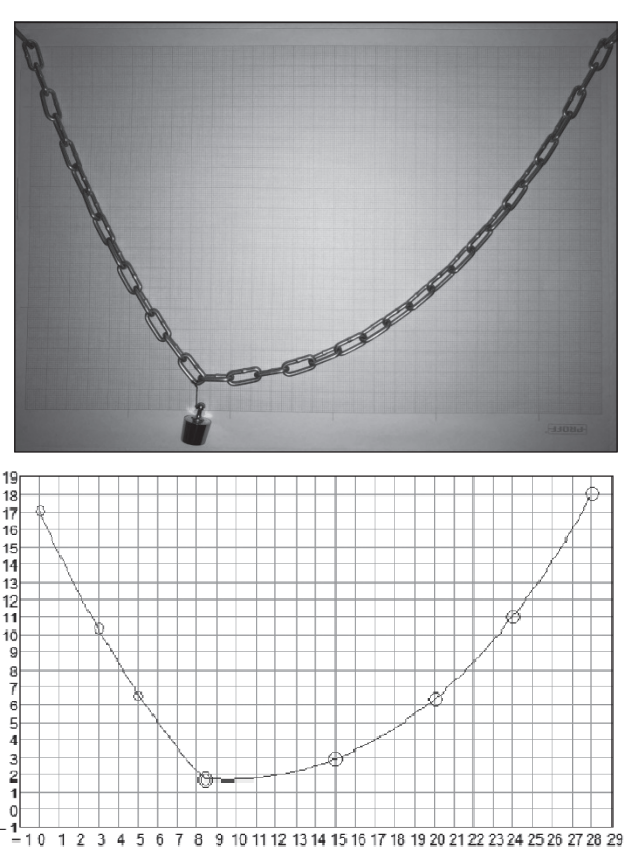
I divide the cable weight into a number of nodes equally distributed along the cable, then add the cable car weight to one of the nodes (the one nearest to the distance that it was added in the original catenary file here, though this can be changed as desired). The nodes are then assumed to be connected by weightless, inextensible links.
It took me some time to get the syntax right! I’ve no doubt an SMath expert could significantly improve the implementation.
CableCar.sm (44,09 КиБ) скачан 824 раз(а).
I enjoy your solution, based on the discretization of the continuum.
As always with such an approach, the results are enough dependent on the input data values and decisions.
I played a little with your tool by introducing (“provoking it”) some limit situations, namely:
• a small or a null cable weight;
• a small or a null “cable car weight”.
Please try such cases and tell us your evaluations. Normally, in this way, some analytical results could be checked (?).
Once again, thanks for your interesting work,
Best regards,
Ioan
WroteHere is my force-balance approach to this problem.
I divide the cable weight into a number of nodes equally distributed along the cable, then add the cable car weight to one of the nodes (the one nearest to the distance that it was added in the original catenary file here, though this can be changed as desired). The nodes are then assumed to be connected by weightless, inextensible links.
It took me some time to get the syntax right! I’ve no doubt an SMath expert could significantly improve the implementation.
CableCar.sm (44,09 КиБ) скачан 824 раз(а).
See please Figures in my article
http://twt.mpei.ac.ru/ochkov/Chain.pdf
WroteHi StvMath,
I enjoy your solution, based on the discretization of the continuum.
As always with such an approach, the results are enough dependent on the input data values and decisions.
I played a little with your tool by introducing (“provoking it”) some limit situations, namely:
• a small or a null cable weight;
• a small or a null “cable car weight”.
Please try such cases and tell us your evaluations. Normally, in this way, some analytical results could be checked (?).
Once again, thanks for your interesting work,
Best regards,
Ioan
Hi Ioan,
Thanks for your comments.
I agree with you that the results are data dependent etc.
The discretisation I used was quite coarse, so I wouldn’t expect good agreement with analytical results in your limiting situations. Of course, a much finer discretisation could, in principle, be used. However, the current model is relatively slow (about 5 seconds on my laptop), and I don’t have the patience to wait for the results of a much finer discretisation!
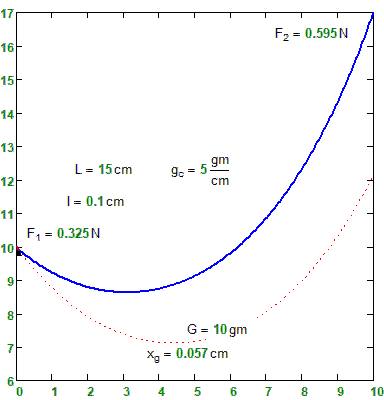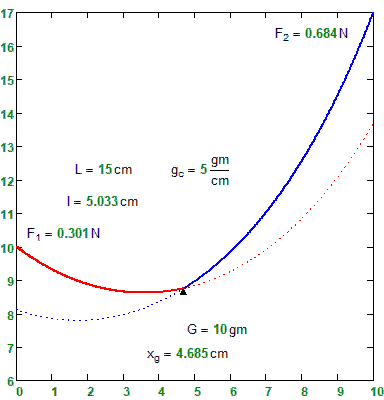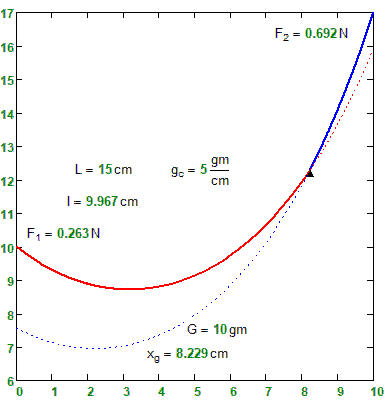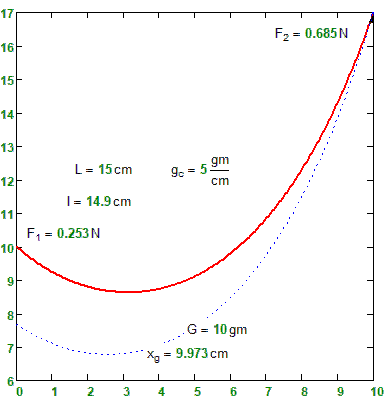
The current model works ok when the cable car weight (G) is set to zero, but the Jacobian crashes if the specific weight (gc) is much below 0.5.
Of course, if SMath had its own Minimize (or Maximize) function we could just have copied Val Ochkov’s original Mathcad approach and saved ourselves the trouble of looking for an alternative method!!
WroteOf course, if SMath had its own Minimize (or Maximize) function
There is lbfgs function for Maxima, it can calculate Minimize.
If it could be implemented to SMath, Minimize problem can be solved.
Regards
(%i1) load("lbfgs" ;
(%o1) /usr/share/maxima/5.47.0/share/lbfgs/lbfgs.mac
(%i2) f(x,y):=(x-y)/((x^2+5)*(y^2+5))+(x^2+y^2)/20000;
2 2
x - y x + y
(%o2) f(x, y) := ----------------- + -------
2 2 20000
(x + 5) (y + 5)
(%i3) lbfgs(f(x,y),[x,y],[1,1],1e-10,[-1,0]);
(%o3) [x = - 1.2860935388262762, y = 1.286093516249451]
;
(%o1) /usr/share/maxima/5.47.0/share/lbfgs/lbfgs.mac
(%i2) f(x,y):=(x-y)/((x^2+5)*(y^2+5))+(x^2+y^2)/20000;
2 2
x - y x + y
(%o2) f(x, y) := ----------------- + -------
2 2 20000
(x + 5) (y + 5)
(%i3) lbfgs(f(x,y),[x,y],[1,1],1e-10,[-1,0]);
(%o3) [x = - 1.2860935388262762, y = 1.286093516249451]- Новые сообщения
- Нет новых сообщений