Hello

My teacher give me a homework, about make a taylor series. Second task is to make something to calculate proper lenght of taylor series.

For example if my function is e(t) how long taylor sieries will be to be equal to this function.

Sorry for my english

I have a idea to make a loop, like 1+1+1+1...1+n until we recive solution, but I dont know how to do that

Hello cube, what's exactly the point?

To build a loop use a for or a while statement (something like in the attachment).

---

Ok guys thanks for such quick response I am surprised and pleased, I found support, it`s means a lot for me. But that is not what I'm looking for

I ll try to explain what im looking for.

Lets say we got a;b;

and we wanna define "c" - what we are looking for b=a if b
after that, once again we check b, then if b=a we recive a solution



So for the Taylor series Im looking for something similar.

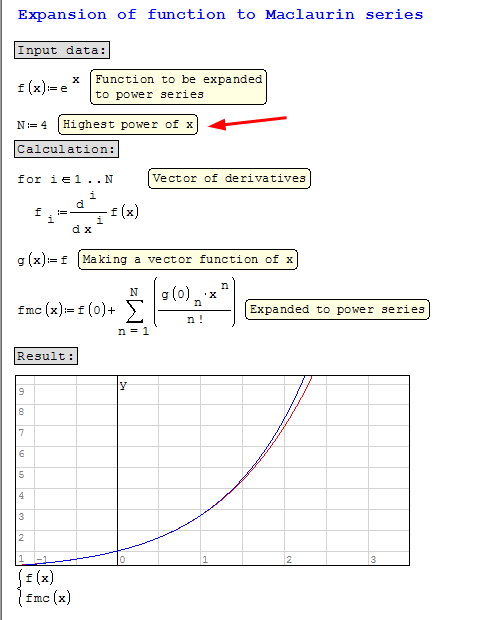
for example x=4 then we look on diagram and see its not equal.

So I put x=5 ok its closser but still its not that what we are looking for.

Putting x=8 yes it fit is close to function between (0;2)

Hello,

Open Help->Examples and choose "Expansion of function to Maclaurin series", than open it. You can then choose the function as well as the highest power of x.

Regards,
Radovan

---

Here is an example which uses the Taylor function of the Nonlinear Solvers plugin and animates approximations of inreasing order.

---