Simple question: how to assign a symbol to the result of symbolical evaluation? Sorry have not found the answer.

E.g. I have some function f(x).
I want to assign another function g(x) to the result of symbolical evaluation of df(x)/dx.

If I assign g(x) to df(x)/dx and make symbolical evaluation, I get correct result, but g(x) is still assigned to df(x)/dx.

Of course, I can symbolically evaluate df(x)/dx and copy the result to the definition of g(x), but then g(x) will not change if the function f(x) changes.

Hello Adventurist !

Welcome to the Smath Community. I don't understand completely
your "assign question". Mybe the answer is in there ?

Jean

ODE_Laplace Read First.sm (37 КиБ) скачан 63 раз(а).

ODE_Laplace 1rst [Type 1].sm (25 КиБ) скачан 47 раз(а).

ODE_Laplace 2nd [Type 3].sm (23 КиБ) скачан 43 раз(а).

ODE_Laplace 1rst [Type 2].sm (24 КиБ) скачан 44 раз(а).

testassign.sm (14 КиБ) скачан 42 раз(а).

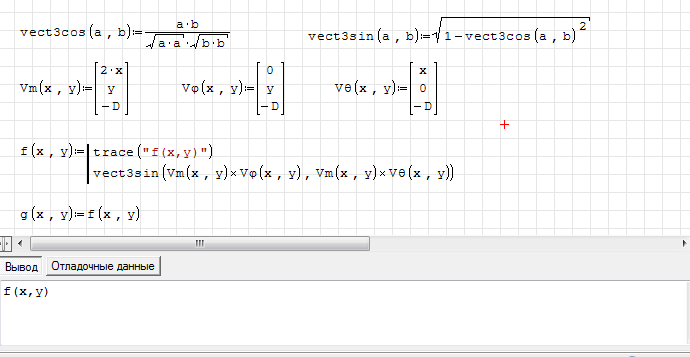
Sorry, have not found the answer. Attached is a sample with two functions f(x,y) and g(x,y).



In the sample I have just copied the result of symbolical evaluation of f(x,y) to g(x,y). How to perform this assignment directly? I need g(x,y) to be updated if input vectors change.

Easy to see that symbolical evaluation does not change f(x,y). Maple can undestand g(x,y) but not f(x,y).

... just assign like this g(x,y):=f(x,y)
shown in red Smath 6179 attached.
Does it work for you ?

Jean

testassign.sm (16 КиБ) скачан 47 раз(а).

maple() function doesn't understand smath cross product symbol. It is not supported in the current version.

Wrote

... just assign like this g(x,y):=f(x,y)
shown in red Smath 6179 attached.
Does it work for you ?

Jean

Hello Jean,

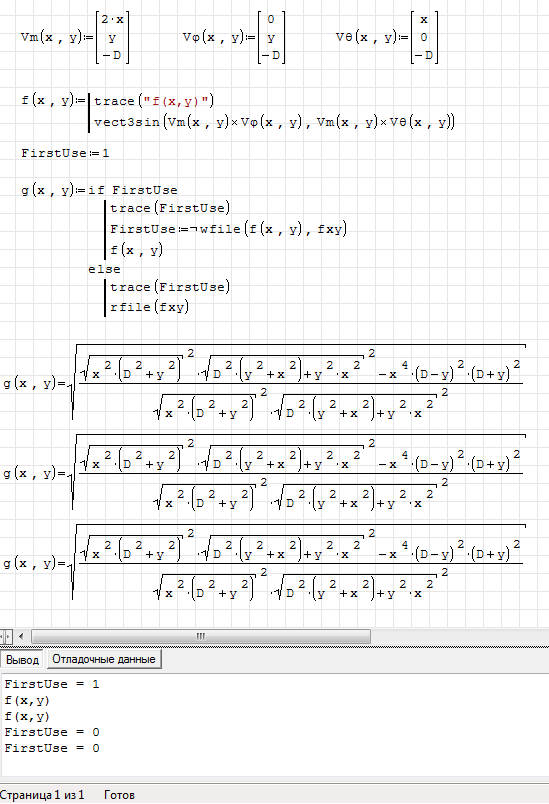
no, it does not work. It assigns original f(x,y) to g(x,y) and not symbolically evaluated, see blue fields in attachment.

testassign1.sm (18 КиБ) скачан 41 раз(а).

@Viacheslav
Hello Viacheslav, yes it is clear, that not everything can be translated to Maple, but this is also not necessary. The question is, how to use existing symbolic evaluation result.

This is necessary not only for Maple. If intermidiate evaluations are not used, with each new definition ALL previously entered definitions must be again and again evaluated.

This works.

testassign_Kr.sm (17 КиБ) скачан 37 раз(а).

Wrote

no, it does not work. It assigns original f(x,y) to g(x,y) and not symbolically evaluated, see blue fields in attachment

The blue is just maple()simplify(...)

The definition of "cross product" goes with the definition
of the coordinates system. There are 24 systems of coordinates.
Typically, Mathcad 11 and earlier is different than Mathematica 4.0.
I don't understand much about "cross product in Smath" whereas
Smath does not have a 3D system except for the horrible 3d QuickPlot.

Jean

Something like this?

Thanks to Martin and Viacheslav for working solutions!

As I understood, there is no regular way in SMath to access already existing result of symbolic evaluation. The solutions are tricks to export the result to string/file and to import it back.

What looks irritating for me, some functions take symbol definition as input, e.g. maple() functions, other functions, like num2str() and wfile(), take the result of symbolic evaluation as input!? Is this the special property of maple() or num2str(), wfile() functions only? If not, how to determine what will given function take as input?

To my point of view, there should be a regular way to access either symbol definition or symbolic evaluation. There is a regular function eval() to get the result of numerical evaluation, why not to implement function like symbeval() to get symbolic evaluation result? Then it will be enough to write

g(x,y):=symbeval(f(x,y))

Wrote

As I understood, there is no regular way in SMath to access already existing result of symbolic evaluation. The solutions are tricks to export the result to string/file and to import it back.

There is no trick spool to file the immediate maple,
no more trick spool back wherever you want.

Jean

Maple series.sm (23 КиБ) скачан 36 раз(а).

... apparently, there is no limits wrt maple.
Added numerical algo "include"

Jean

Genfit Algo Include.sm (13 КиБ) скачан 44 раз(а).

Genfit Algo Include Test.sm (16 КиБ) скачан 44 раз(а).

Maple series.sm (32 КиБ) скачан 37 раз(а).

... as far as I understand: you request for TWO cross-product.
In fact, there are more that you can collect/spool to file.

testassign_Kr.sm (11 КиБ) скачан 41 раз(а).

Jean,

thank you for a lot of examples, but this is not about maple and not about cross-products. Also it is absolutely clear how to export/import strings or files. This is a general question for any symbolical system: how to distinguish between the symbol definition and its symbolical evaluation.

For some reason maple() and for sure some other functions take symbol definition as input. Other functions, like str2num() or wfile() use already symbolically evaluated expression (or may be they evaluate it internally?). There is no function or operator, which will say: here I want my original f(x,y) with cross products (by the way, how to write it to the file?) and here I want already symbollicaly evaluated and simplified result.

My suggestion was to implement some operator or function, like symbeval(), which returns the same as right arrow operator (Ctrl-.). Then the user can specify what exactly is passed to the function, definition, etc. Should I duplicate this to feature requests?

Hello,

Wrote

My suggestion was to implement some operator or function, like symbeval(), which returns the same as right arrow operator (Ctrl-.). Then the user can specify what exactly is passed to the function, definition, etc. Should I duplicate this to feature requests?

I agree with you and I think that this question might be a future request for Andrey. I remember that eval() was introduced long time ago due to the well known symbolic-numeric problems. In the meantime there were symbolic engine plugins introduced (maple and Maxima) and I think that your suggestion about symbeval() is worth considering as well. To be honest, I do not know why this problem appeared after such a long time.

Regards,
Radovan

Wrote

My suggestion was to implement some operator or function, like symbeval(), which returns the same as right arrow operator (Ctrl-.). Then the user can specify what exactly is passed to the function, definition, etc. Should I duplicate this to feature requests?

No need to put in "feature request", because it is already implemented.

1. Laplace Ode posted does exactly that
2. Symbolic can be spooled to file.

Smath is not a "scalar system". That is takes ln(x) and plot QuickPlot
is not scalar but vector. A more complex formula would execute faster
from eval(,) because it sets the algorithm from formula into the executable
suite from eval(,) which in fact is from the symbolic internal expansion.

"scalar" was just explained few days ago [What is scalar]. Most if not all
Smath functions are borrowed from various codes, thus not uniformized
unlike Mathcad/Mathsoft. A scalar algorithm runs by itself on its internal
x, y ... scalar iterator(s), so will not run on Smath that has only vector
input(s) for the variables. Revisit the "Fourier Quantum 2C" just posted.
Mathcad runs the integral product, no way Smath can/could. Once the system
of integral is solved, it can take Smath vector inputs.

Whether a "scalar interpreter" is desirable ? NOT SURE. It would return
Smath to the design board and beta testing for a long times because to
few users. By same token, might scrap lot more from the existing 6179
that works so fine. The result you show, is to me, strictly a bug by
coincidence, if you want to assign the result of cross products you
must isolate in vector as I have done. If afterwards you want to
recombine, you must do it again ... symbolic[1 x symbolic[2

Since the very birthday of Mathcad/Mathsoft, some inconvenience remained
over the years of > 125000 Collabs + unreported visitors. Some attachment
[Mathcad work sheets] got read 2000 times in two days.
Some functions could not be chained, some had to be recopied ...

On the other hand, Smath is far more educative than Mathcad, why ?
In Smath you can't do what you can't explicit. Probably the best
educative tool you could wish, in the sense of doing so much advanced
maths Sciences/Engineering.

Cheers, Jean

Wrote

No need to put in "feature request", because it is already implemented.

Yes, of course symbolic evaluation is implemented, but how to assign the result to the symbol?

Wrote

1. Laplace Ode posted does exactly that

Sorry, can you show the place, where symbolically evaluated result is assigned. I have not found it...

Start with a simple example, note this:
as you type int(1/(1+x^2),x) it shows
the symbol of the indefinite integral.

Jean

Symbolic assign.sm (3 КиБ) скачан 43 раз(а).

Hello,

I might be wrong here, but I think the question is about something like this regarding maple.
If you can not reproduce this, there might be something wrong with my SMath.



Regadrs,
Radovan

This is bug in maple() function. Not all operations are performed correctly during the conversion.