1 страниц (12 вхождений)
Треугольник Серпинского - Сообщения
#1 Опубликовано: 19.10.2010 13:28:18
Россия навсегда!
Вячеслав Мезенцев
2 пользователям понравился этот пост
#2 Опубликовано: 19.10.2010 13:31:20
Круто!
#3 Опубликовано: 19.10.2010 13:39:34
Народу нравится 
Пришлось покумекать немного. Какая-то проблема с augment():
так работает
а вот так не работает:
По-моему, это называется нереентерабельность Функции DOS не могли использовать сами себя, т.к. использовали при передаче параметров не стек, а регистры процессора.
Функции DOS не могли использовать сами себя, т.к. использовали при передаче параметров не стек, а регистры процессора.
Пришлось покумекать немного. Какая-то проблема с augment():
так работает
augment(1;2)augment(1;augment(1;2))По-моему, это называется нереентерабельность
Россия навсегда!
Вячеслав Мезенцев
#4 Опубликовано: 19.10.2010 14:41:14
Желающие разобраться в алгоритме могут доделать Ковёр Серпинского. Мне стало лень, слишком долго считает.

Документ: Ковёр Серпинского
Документ: Ковёр Серпинского
Россия навсегда!
Вячеслав Мезенцев
1 пользователям понравился этот пост
Serg 25.01.2014 12:52:00
#5 Опубликовано: 19.10.2010 16:04:47
Замечательный тест программы, спасибо! Разберусь в чём причина медленных расчётов в данном случае - думаю, смогу ускорить. Кстати, в треугольнике Серпинского если в контекстном меню включить численную оптимизацию (ну или использовать eval(..), что, по сути, аналогично) для определения S (S:=Sp(n)), то производительность вырастет почти в два раза.
Это та же беда, что и со стеком: функция отказывается принимать одновременно скаляр с вектором в аргументах...
Ещё раз спасибо!
WroteПришлось покумекать немного. Какая-то проблема с augment()
Это та же беда, что и со стеком: функция отказывается принимать одновременно скаляр с вектором в аргументах...
Ещё раз спасибо!
#6 Опубликовано: 19.10.2010 23:37:05
WroteWroteКакая-то проблема с augment()
Это та же беда, что и со стеком: функция отказывается принимать одновременно скаляр с вектором в аргументах...
Там оба аргумента векторы, точнее даже матрицы. Я привёл не тот пример.
Это работает:
[MATH]T(x)←line(a←augment(x+el(x;1);x+el(x;2));augment(x;a);2;1)[/MATH]
А это нет:
[MATH]T(x)←augment(x;augment(x+el(x;1);x+el(x;2)))[/MATH]
Причём, без определения функции это считается:
augment(v; augment(v+el(v;1);v+el(v;2)))Россия навсегда!
Вячеслав Мезенцев
#7 Опубликовано: 20.10.2010 06:09:57
Документ: Треугольник Серпинского 3D.sm
П.С. Нужно поколдовать с порядком перемещения пирамид, чтобы не было артефактов.
Россия навсегда!
Вячеслав Мезенцев
1 пользователям понравился этот пост
Serg 25.01.2014 12:52:00
#8 Опубликовано: 20.10.2010 06:51:33
Предлагаю использовать "Ковёр Серпинского" в тесте производительности версий 
з.ы. на моей машине считался 8мин. 33 сек.
з.ы. на моей машине считался 8мин. 33 сек.
Не официальный справочник http://sites.google.com/site/mikkhalichlab/
jabber конференция smath@conference.jabber.ru
#9 Опубликовано: 23.10.2010 14:56:27
Работаю над ускорением вычислений и выяснил, что в данных примерах основное время вычисления программа тратит на получение элементов матрицы S (т.к. матрица очень большая, а в общем случае получить элемент матрицы можно только разобрав её полностью, из-за чего и начинаются тормоза). Из этого, кстати, следует, что если минимизировать количество обращений к элементам матрицы, то и скорость вычислений существенно возрастёт (это справедливо до и после оптимизации в коде), а в цикле G(x) кол-во таких обращений можно уменьшить с шести до двух.
Делюсь промежуточными результатами оптимизации кода (см. время вычислений внизу):
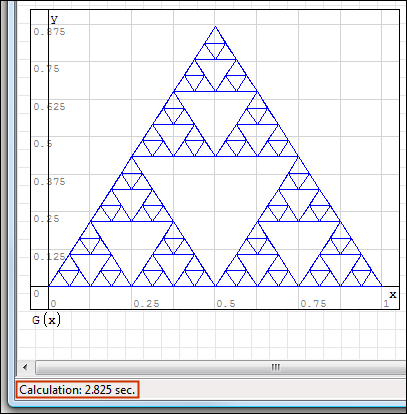

Что бы получить похожие результаты достаточно распаковать SpecialFunctions.1_2_3948.Plugin.Bin.zip плагин и заменить им предыдущую версию из папки plugins в установочной директории SMath Studio. Оптимизированные версии файлов: TreugolnikSerpinskogo.mod2.sm, KoverSerpinskogo.mod2.sm.
P.S.: И это не предел. Не всё удалось вынести в плагин - некоторой оптимизации подверглось и ядро, т.ч. в новой версии SMath Studio процесс будет идти ещё быстрее.
С уважением, Андрей Ивашов.
Делюсь промежуточными результатами оптимизации кода (см. время вычислений внизу):
Что бы получить похожие результаты достаточно распаковать SpecialFunctions.1_2_3948.Plugin.Bin.zip плагин и заменить им предыдущую версию из папки plugins в установочной директории SMath Studio. Оптимизированные версии файлов: TreugolnikSerpinskogo.mod2.sm, KoverSerpinskogo.mod2.sm.
P.S.: И это не предел. Не всё удалось вынести в плагин - некоторой оптимизации подверглось и ядро, т.ч. в новой версии SMath Studio процесс будет идти ещё быстрее.
С уважением, Андрей Ивашов.
3 пользователям понравился этот пост
#10 Опубликовано: 03.02.2012 01:20:51
WroteПредлагаю использовать "Ковёр Серпинского" в тесте производительности версий
з.ы. на моей машине считался 8мин. 33 сек.
В версии 0.91 на той же машине 2 мин 21 сек!
Прогресс на лицо или на лице
Не официальный справочник http://sites.google.com/site/mikkhalichlab/
jabber конференция smath@conference.jabber.ru
#11 Опубликовано: 17.04.2012 17:22:45
Россия навсегда!
Вячеслав Мезенцев
4 пользователям понравился этот пост
Mikka 18.04.2012 13:19:00, Fridel Selitsky 18.04.2012 00:57:00, Serg 25.01.2014 12:53:00, kmihaylovich 19.04.2012 02:27:00
#12 Опубликовано: 22.04.2012 05:03:53
Дерево Пифагора

Документ: Pythagoras Tree.sm
Примечание. Очень долго считает. При ограничении размера конечной ветки до 0,1 считает около 1 минуты у меня.
Документ: Pythagoras Tree.sm
Примечание. Очень долго считает. При ограничении размера конечной ветки до 0,1 считает около 1 минуты у меня.
Россия навсегда!
Вячеслав Мезенцев
1 пользователям понравился этот пост
Serg 25.01.2014 12:53:00
1 страниц (12 вхождений)
- Новые сообщения
- Нет новых сообщений
