Hi guys.

I have come across an obstacle that I have not managed to find a satisfactory solution to. I am sure the problem is easy for the experts here, but the solution completely eludes me.

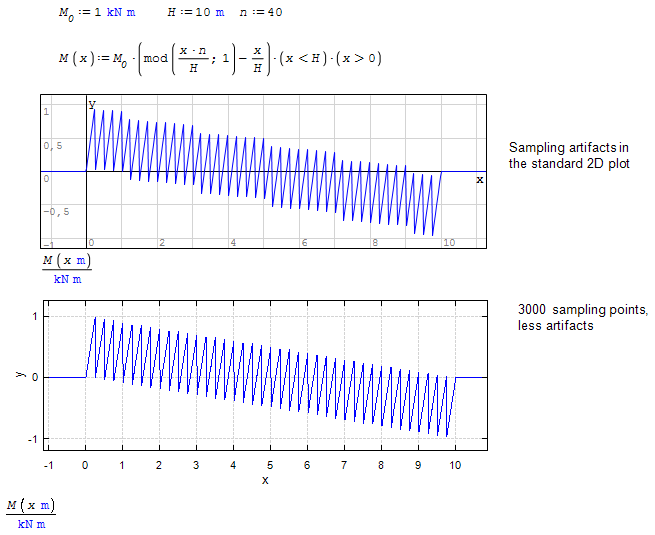
I want to make a function to plot bending moments caused by an eccentric load.

My aim is to make an equation/function that can plot a continuous bending moment diagram, while being able to scale how many loads is acting on the member.

Thank you for your time.

Best regards,
Hans Kristian.



test.sm (106 KiB) downloaded 84 time(s).

Do you mean a function that will represent M(x)... up to 100 ?
Certainly from selecting representative support points !



test (3).sm (108 KiB) downloaded 82 time(s).

Wrote

Do you mean a function that will represent M(x)... up to 100 ?
Certainly from selecting representative support points !



test (3).sm (108 KiB) downloaded 82 time(s).

Hi Jean,

I want a function that will represent M(x) where the eccentric load P will be divided into n equal loads which are spaced out evenly along the length of the member.

Does that make sense?

saw.sm (7 KiB) downloaded 82 time(s).

Wrote

Hi Jean,

I want a function that will represent M(x) where the eccentric load P will be divided into n equal loads which are spaced out evenly along the length of the member.

I guess it makes sense, that stuff is not my cup of tea.
You mean the 100 lines is typical of eccentric load model but
each one will be of different parameters [your conditions] ???
Big project in view Captain !
We have a utility that divides a range in N equal spaces>
That will make some lines longer/shorter as per the how those
loads appear on the beam.
Do you have some material from else source ?

Now with proper scaling


saw1.sm (5 KiB) downloaded 91 time(s).

Wrote

Wrote

Hi Jean,

I want a function that will represent M(x) where the eccentric load P will be divided into n equal loads which are spaced out evenly along the length of the member.

I guess it makes sense, that stuff is not my cup of tea.
You mean the 100 lines is typical of eccentric load model but
each one will be of different parameters [your conditions] ???
Big project in view Captain !
We have a utility that divides a range in N equal spaces>
That will make some lines longer/shorter as per the how those
loads appear on the beam.
Do you have some material from else source ?

The application for this sheet is going to be on sandwich concrete wall panels where the weight of the exterior non-bearing layer of concrete acts on the interior bearing layer. The actions to consider are N and M.

In practical application, N will be split into 2-4 equal loads, but I wanted to make a framework that could split the load into n parts, just for fun.. :d

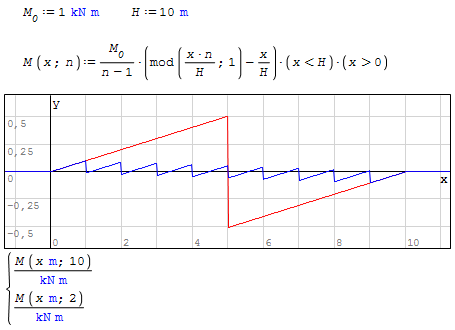
Wrote

Now with proper scaling


saw1.sm (5 KiB) downloaded 91 time(s).

Thank you Martin, this is exactly what I am looking for!

Although your expression is both much simpler and much faster to compute, it does not look anything like what I had in mind.. Goes to show I have so much more to learn when it comes to SMath!

Cheers!

Wrote

Now with proper scaling

Just for show why the Martin solution it's correct:



Best regards.
Alvaro.

Wrote

Thank you Martin, this is exactly what I am looking for!

Although your expression is both much simpler and much faster to compute, it does not look anything like what I had in mind.. Goes to show I have so much more to learn when it comes to SMath!

Cheers!

The approach was purely phenomenological, i.e. to reproduce the plots, no matter what they mean. The idea was to combine a sawtooth function and a linear term (slope). There are many options to get a sawtooth, the modulo function being just one of them. Others are round(), Floor(), Ceil()... The remainder was guessing the coefficients in a heuristic trial and error fashion.

Wrote

Although your expression is both much simpler and much faster to compute, it does not look anything like what I had in mind..

That great scaled saw tooth plots on the canvas wrt 'x'.
You then have to subdivide 'x' to imitate your first document.
The attached utilities are general rather than specific to
your project. You can fabricate whatever for purpose.
Stay in love with Smath ... don't hesitate for +.
Cheers ... Jean

Utilities Discrete Algo Range INTERVALS.sm (29 KiB) downloaded 90 time(s).
Utilities Discrete Algo Range INTERVALS Application.sm (29 KiB) downloaded 88 time(s).
Utilities Discrete Algo Range INTERVALS Parts 1234.sm (84 KiB) downloaded 91 time(s).

Wrote

Wrote

Now with proper scaling

Just for show why the Martin solution it's correct:

Best regards.
Alvaro.

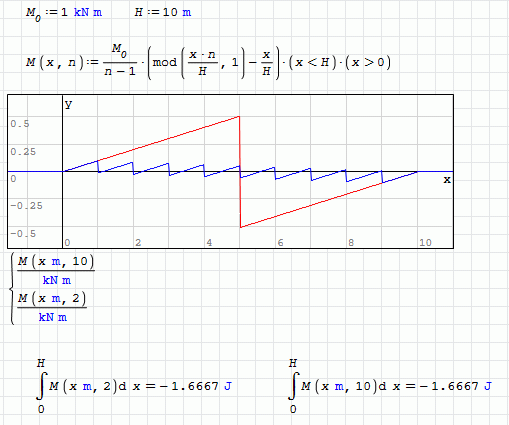
Interessting. I have tweaked Martins equations - now n represents the number of loads, not the number of segments between loads/supports.

Any idea why the integral gives me this result? Also, my integral is 10x the value of yours.

Best regards,

Wrote

Wrote

Although your expression is both much simpler and much faster to compute, it does not look anything like what I had in mind..

That great scaled saw tooth plots on the canvas wrt 'x'.
You then have to subdivide 'x' to imitate your first document.
The attached utilities are general rather than specific to
your project. You can fabricate whatever for purpose.
Stay in love with Smath ... don't hesitate for +.
Cheers ... Jean

Utilities Discrete Algo Range INTERVALS.sm (29 KiB) downloaded 90 time(s).
Utilities Discrete Algo Range INTERVALS Application.sm (29 KiB) downloaded 88 time(s).
Utilities Discrete Algo Range INTERVALS Parts 1234.sm (84 KiB) downloaded 91 time(s).

Interesting stuff.. I will have a closer look at that when I have some spare time.

Cheers :d

Wrote

Wrote

Thank you Martin, this is exactly what I am looking for!

Although your expression is both much simpler and much faster to compute, it does not look anything like what I had in mind.. Goes to show I have so much more to learn when it comes to SMath!

Cheers!

The approach was purely phenomenological, i.e. to reproduce the plots, no matter what they mean. The idea was to combine a sawtooth function and a linear term (slope). There are many options to get a sawtooth, the modulo function being just one of them. Others are round(), Floor(), Ceil()... The remainder was guessing the coefficients in a heuristic trial and error fashion.

I thought that might be the case.. Anyways, it was purely to illustrate what happens when n approaches infinity, and your solution worked wonders for that!

Thanks again

Wrote

Any idea why the integral gives me this result?

Smath native Simpson integrator ranges from:
1. Exact only few trivial cases.
2. Acceptable but depending upon Options/Calculations/Int. acc
set 1000 in your example.
3. Native Simpson may be TOTALLY useless.
Sooner or later, units system collide in the wall.

Discontinuous integration is poison in the soup.
Master tool box has done all difficult projects
except ONE ... The Inverse_Z transform.

Cheers ... Jean

Integrate Discontinuous [min(x)].sm (8 KiB) downloaded 87 time(s).
Integrate Discontinuous_1.sm (24 KiB) downloaded 83 time(s).
Integrate Discontinuous.sm (31 KiB) downloaded 83 time(s).
Integrate Discontinuous_2.sm (132 KiB) downloaded 84 time(s).
Integral 00000000 MASTER ToolBox.sm (476 KiB) downloaded 88 time(s).

Wrote

Wrote

Any idea why the integral gives me this result?

Smath native Simpson integrator ranges from:
1. Exact only few trivial cases.
2. Acceptable but depending upon Options/Calculations/Int. acc
set 1000 in your example.
3. Native Simpson may be TOTALLY useless.
Sooner or later, units system collide in the wall.

Discontinuous integration is poison in the soup.
Master tool box has done all difficult projects
except ONE ... The Inverse_Z transform.

Cheers ... Jean

Thanks again Jean.. I am baffled by the knowledge you guys possess here on the forum!

Best regards,
Hans Kristian.

Wrote

Thanks again Jean.. I am baffled by the knowledge you guys possess here on the forum!

At least, two of us are old kookoo from Mathcad.
Smath learning curve has not revealed asymptotic.
Two versions of the 3D rolling Torus.

Rotate Torus [Ber7 20170922].sm (20 KiB) downloaded 85 time(s).
Rotate Torus.sm (44 KiB) downloaded 82 time(s).

Wrote

Wrote

Thanks again Jean.. I am baffled by the knowledge you guys possess here on the forum!

At least, two of us are old kookoo from Mathcad.
Smath learning curve has not revealed asymptotic.
Two versions of the 3D rolling Torus.

It took my computer about 3 minutes to compute this sheet..