Function and for loop - Сообщения
I have come across an obstacle that I have not managed to find a satisfactory solution to. I am sure the problem is easy for the experts here, but the solution completely eludes me.
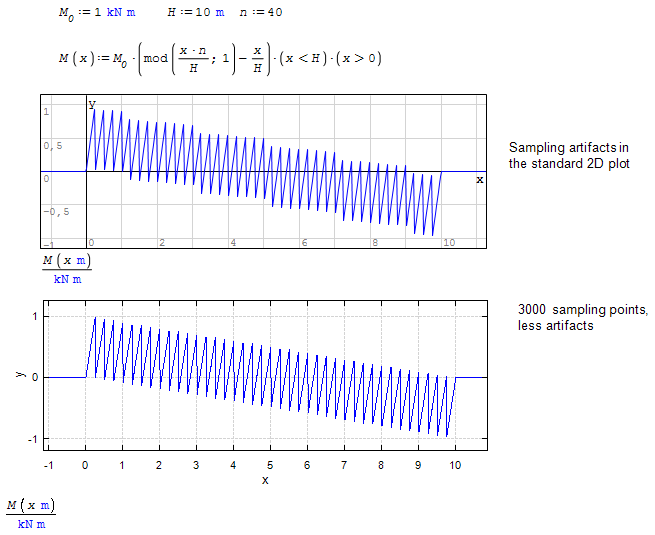
I want to make a function to plot bending moments caused by an eccentric load.
My aim is to make an equation/function that can plot a continuous bending moment diagram, while being able to scale how many loads is acting on the member.
Thank you for your time.
Best regards,
Hans Kristian.
test.sm (106,56 КиБ) скачан 614 раз(а).
Certainly from selecting representative support points !
test (3).sm (108,92 КиБ) скачан 575 раз(а).
WroteDo you mean a function that will represent M(x)... up to 100 ?
Certainly from selecting representative support points !
test (3).sm (108,92 КиБ) скачан 575 раз(а).
Hi Jean,
I want a function that will represent M(x) where the eccentric load P will be divided into n equal loads which are spaced out evenly along the length of the member.
Does that make sense?
WroteHi Jean,
I want a function that will represent M(x) where the eccentric load P will be divided into n equal loads which are spaced out evenly along the length of the member.
I guess it makes sense, that stuff is not my cup of tea.
You mean the 100 lines is typical of eccentric load model but
each one will be of different parameters [your conditions] ???
Big project in view Captain !
We have a utility that divides a range in N equal spaces>
That will make some lines longer/shorter as per the how those
loads appear on the beam.
Do you have some material from else source ?
WroteWroteHi Jean,
I want a function that will represent M(x) where the eccentric load P will be divided into n equal loads which are spaced out evenly along the length of the member.
I guess it makes sense, that stuff is not my cup of tea.
You mean the 100 lines is typical of eccentric load model but
each one will be of different parameters [your conditions] ???
Big project in view Captain !
We have a utility that divides a range in N equal spaces>
That will make some lines longer/shorter as per the how those
loads appear on the beam.
Do you have some material from else source ?
The application for this sheet is going to be on sandwich concrete wall panels where the weight of the exterior non-bearing layer of concrete acts on the interior bearing layer. The actions to consider are N and M.
In practical application, N will be split into 2-4 equal loads, but I wanted to make a framework that could split the load into n parts, just for fun.. :d
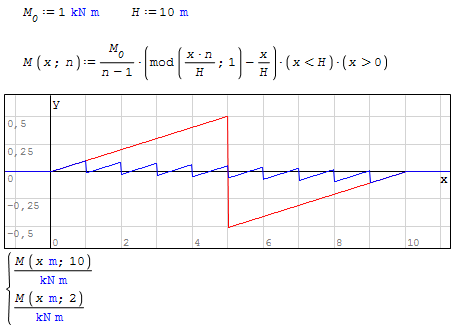
WroteNow with proper scaling
saw1.sm (5,15 КиБ) скачан 599 раз(а).
Thank you Martin, this is exactly what I am looking for!
Although your expression is both much simpler and much faster to compute, it does not look anything like what I had in mind.. Goes to show I have so much more to learn when it comes to SMath!
Cheers!
Wrote
Thank you Martin, this is exactly what I am looking for!
Although your expression is both much simpler and much faster to compute, it does not look anything like what I had in mind.. Goes to show I have so much more to learn when it comes to SMath!
Cheers!
The approach was purely phenomenological, i.e. to reproduce the plots, no matter what they mean. The idea was to combine a sawtooth function and a linear term (slope). There are many options to get a sawtooth, the modulo function being just one of them. Others are round(), Floor(), Ceil()... The remainder was guessing the coefficients in a heuristic trial and error fashion.
WroteAlthough your expression is both much simpler and much faster to compute, it does not look anything like what I had in mind..
That great scaled saw tooth plots on the canvas wrt 'x'.
You then have to subdivide 'x' to imitate your first document.
The attached utilities are general rather than specific to
your project. You can fabricate whatever for purpose.
Stay in love with Smath ... don't hesitate for +.
Cheers ... Jean
Utilities Discrete Algo Range INTERVALS.sm (29,58 КиБ) скачан 613 раз(а).
Utilities Discrete Algo Range INTERVALS Application.sm (29,6 КиБ) скачан 585 раз(а).
Utilities Discrete Algo Range INTERVALS Parts 1234.sm (84,91 КиБ) скачан 603 раз(а).
WroteWroteNow with proper scaling
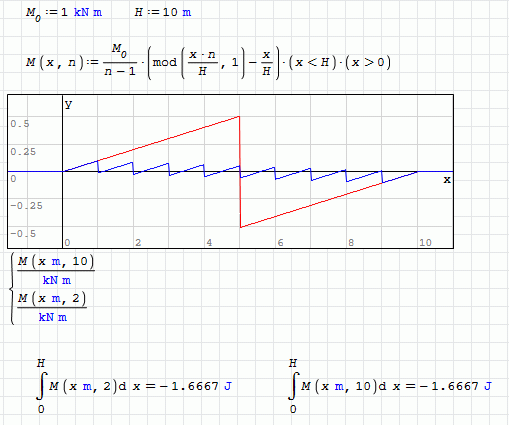
Just for show why the Martin solution it's correct:
Best regards.
Alvaro.
Interessting. I have tweaked Martins equations - now n represents the number of loads, not the number of segments between loads/supports.
Any idea why the integral gives me this result? Also, my integral is 10x the value of yours.
Best regards,
WroteWroteAlthough your expression is both much simpler and much faster to compute, it does not look anything like what I had in mind..
That great scaled saw tooth plots on the canvas wrt 'x'.
You then have to subdivide 'x' to imitate your first document.
The attached utilities are general rather than specific to
your project. You can fabricate whatever for purpose.
Stay in love with Smath ... don't hesitate for +.
Cheers ... Jean
Utilities Discrete Algo Range INTERVALS.sm (29,58 КиБ) скачан 613 раз(а).
Utilities Discrete Algo Range INTERVALS Application.sm (29,6 КиБ) скачан 585 раз(а).
Utilities Discrete Algo Range INTERVALS Parts 1234.sm (84,91 КиБ) скачан 603 раз(а).
Interesting stuff.. I will have a closer look at that when I have some spare time.
Cheers :d
WroteWrote
Thank you Martin, this is exactly what I am looking for!
Although your expression is both much simpler and much faster to compute, it does not look anything like what I had in mind.. Goes to show I have so much more to learn when it comes to SMath!
Cheers!
The approach was purely phenomenological, i.e. to reproduce the plots, no matter what they mean. The idea was to combine a sawtooth function and a linear term (slope). There are many options to get a sawtooth, the modulo function being just one of them. Others are round(), Floor(), Ceil()... The remainder was guessing the coefficients in a heuristic trial and error fashion.
I thought that might be the case.. Anyways, it was purely to illustrate what happens when n approaches infinity, and your solution worked wonders for that!
Thanks again
WroteAny idea why the integral gives me this result?
Smath native Simpson integrator ranges from:
1. Exact only few trivial cases.
2. Acceptable but depending upon Options/Calculations/Int. acc
set 1000 in your example.
3. Native Simpson may be TOTALLY useless.
Sooner or later, units system collide in the wall.
Discontinuous integration is poison in the soup.
Master tool box has done all difficult projects
except ONE ... The Inverse_Z transform.
Cheers ... Jean
Integrate Discontinuous [min(x)].sm (8,56 КиБ) скачан 479 раз(а).
Integrate Discontinuous_1.sm (24,52 КиБ) скачан 564 раз(а).
Integrate Discontinuous.sm (31,18 КиБ) скачан 588 раз(а).
Integrate Discontinuous_2.sm (132,47 КиБ) скачан 580 раз(а).
Integral 00000000 MASTER ToolBox.sm (476,63 КиБ) скачан 572 раз(а).
WroteWroteAny idea why the integral gives me this result?
Smath native Simpson integrator ranges from:
1. Exact only few trivial cases.
2. Acceptable but depending upon Options/Calculations/Int. acc
set 1000 in your example.
3. Native Simpson may be TOTALLY useless.
Sooner or later, units system collide in the wall.
Discontinuous integration is poison in the soup.
Master tool box has done all difficult projects
except ONE ... The Inverse_Z transform.
Cheers ... Jean
Thanks again Jean.. I am baffled by the knowledge you guys possess here on the forum!
Best regards,
Hans Kristian.
WroteThanks again Jean.. I am baffled by the knowledge you guys possess here on the forum!
At least, two of us are old kookoo from Mathcad.
Smath learning curve has not revealed asymptotic.
Two versions of the 3D rolling Torus.
Rotate Torus [Ber7 20170922].sm (20,51 КиБ) скачан 479 раз(а).
Rotate Torus.sm (44,41 КиБ) скачан 586 раз(а).
WroteWroteThanks again Jean.. I am baffled by the knowledge you guys possess here on the forum!
At least, two of us are old kookoo from Mathcad.
Smath learning curve has not revealed asymptotic.
Two versions of the 3D rolling Torus.
It took my computer about 3 minutes to compute this sheet..
- Новые сообщения
- Нет новых сообщений