1 Pages (4 items)
zero-point of e-Function - Messages
#1 Posted: 2/18/2016 4:48:51 AM
Hello everyone,
I stumbled over a zero-Point Problem...
I attached a Picture of my Problem.
I wanted to calculate the Zero-Point of f(x)=-e^(x/33)+6. The Programm says that there are no "real" Zero Points.
So I played around a Little bit and found out that when the Exponent reaches 0.091 ->0.09 the error occurs.
Do you guys have any guesses or did I found a bug in here?
Thanks
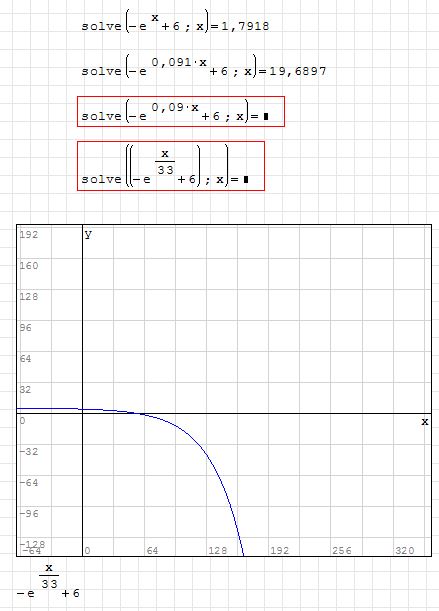
I stumbled over a zero-Point Problem...
I attached a Picture of my Problem.
I wanted to calculate the Zero-Point of f(x)=-e^(x/33)+6. The Programm says that there are no "real" Zero Points.
So I played around a Little bit and found out that when the Exponent reaches 0.091 ->0.09 the error occurs.
Do you guys have any guesses or did I found a bug in here?
Thanks
#2 Posted: 2/18/2016 5:30:51 AM
It is not a bug. You simply set correctly
Tools--> Options --> Calculation --> Roots (range)
sergio
Tools--> Options --> Calculation --> Roots (range)
sergio
2 users liked this post
#3 Posted: 2/18/2016 6:55:39 AM
Thank you very much!
I am new to the Programm and did not know (and why?) there were an upper and lower range of the roots.
The topic can be deleted..
I am new to the Programm and did not know (and why?) there were an upper and lower range of the roots.
The topic can be deleted..
#4 Posted: 2/18/2016 12:16:55 PM
No, don't delete the topic. Answer is correct, it doctored the case.
Some very flat functions may not find roots even in advanced CAS [Computer Algebra System].
Smath 32 bits, not 64 extended floating point does not help either.
More generally, computing machinery are limited by their "ulp" [Unit in Last Place].
"ulp" => read as popular "granularity". Between two machine numbers to close together
the system zigzag eternally, but they all have an internal error detect.
"No real root" is a typical Smath error message.
Jean
Some very flat functions may not find roots even in advanced CAS [Computer Algebra System].
Smath 32 bits, not 64 extended floating point does not help either.
More generally, computing machinery are limited by their "ulp" [Unit in Last Place].
"ulp" => read as popular "granularity". Between two machine numbers to close together
the system zigzag eternally, but they all have an internal error detect.
"No real root" is a typical Smath error message.
Jean
1 Pages (4 items)
- New Posts
- No New Posts
