Hello everyone,

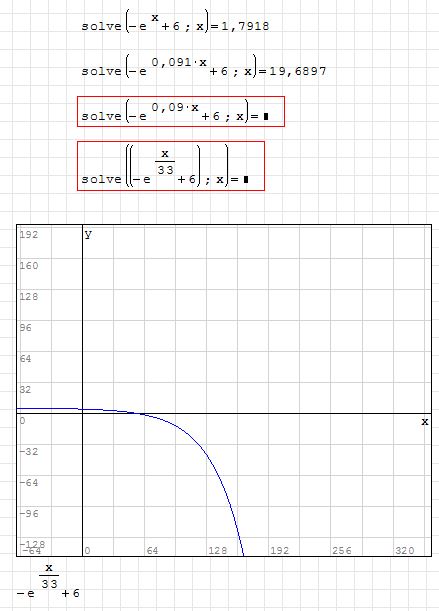
I stumbled over a zero-Point Problem...

I attached a Picture of my Problem.

I wanted to calculate the Zero-Point of f(x)=-e^(x/33)+6. The Programm says that there are no "real" Zero Points.
So I played around a Little bit and found out that when the Exponent reaches 0.091 ->0.09 the error occurs.

Do you guys have any guesses or did I found a bug in here?

Thanks

It is not a bug. You simply set correctly
Tools--> Options --> Calculation --> Roots (range)

sergio

Thank you very much!

I am new to the Programm and did not know (and why?) there were an upper and lower range of the roots.

The topic can be deleted..

No, don't delete the topic. Answer is correct, it doctored the case.
Some very flat functions may not find roots even in advanced CAS [Computer Algebra System].
Smath 32 bits, not 64 extended floating point does not help either.
More generally, computing machinery are limited by their "ulp" [Unit in Last Place].
"ulp" => read as popular "granularity". Between two machine numbers to close together
the system zigzag eternally, but they all have an internal error detect.
"No real root" is a typical Smath error message.

Jean