Анимация механизмов с двумя и более степенями свободы методом А. Б. Иванова
Поясняющий пример.
Механизм,который состоит из кривошипа,двух шатунов и ползуна,
приводится в движение кривошипом. Найти все положения механизма
за один полный оборот кривошипа.
Будем использовать предложенный А.Б. Ивановым метод,который
состоит в следующем.
Выберем из шести координат,определяющих положение механизма,
две,например, одну из координат конца кривошипа(х1) и координату
ползуна(х6).Чтобы перевести звенья механизма из положения,которое
он занимает в момент времени t и которое соответствует значениям
двух координат х1, х6 , в положение бесконечно близкое, которое он
занимает в момент времени t +dt,и которое соответствует координатам
x1+dx1 ,x6+dx6 ,можно поступить следующим образом.
Сначала зафиксируем координату х1,т.е. к четырем уравнениям
геометрических связей добавим пятое уравнение х1=0,и переместим
ползун на величину dx6.Тогда х6 увеличится,а х1 не изменится.Затем
переместим конец кривошипа на величину dx1,и зафиксируем ползун
,т.е.пятым уравнением теперь будет х6=0.
Повторяем эту процедуру до тех пор,пока не найдем все положения
механизма.
Отметим,что поскольку две координаты из шести выбираются произвольно
и произвольно устанавливается порядок их чередования,то существует
множество решений,два из которых представлены на анимациях.

---

Primer.pdf (157 KiB) downloaded 320 time(s).

Плоский трехзвенный манипулятор1.(Planar three-link manipulator)


Плоский трехзвенный манипулятор2

---

2RC-2polsuna.smz (8 KiB) downloaded 152 time(s).

Вращающийся двухзвенный манипулятор

---

Puma Pl1.smz (68 KiB) downloaded 120 time(s).

Здравствуйте. У меня вопрос про трехзвенный манипулятор1. В ваших примерах точки проходят всю траекторию, а здесь нет. Как можно получить замкнутую траекторию для 12 или 56. Так же при изменении места уравнения в системе, изменяется сам вид анимации, якобиан и определитель. Может ли это быть связано с степенью свободы системы больше одной?

Выбрал комбинацию поочередных закреплений,которая заставляет концевую точку манипулятора проходить всю траекторию:

Сразу отмечу, что мои познания в математике основаны на институтских курсах. При изменении места уравнений в механизме с шатуном, трехмерном манипуляторе, плоском манипуляторе2 движение стало инверсным. Бесконечность решений воспринимаю как векторное поле, где при задании константы получаем кривую вдоль, которой двигаемся при изменение времени. Хотелось бы узнать условие при котором движение по заданной траектории было с неотрицательной скоростью. Помню про скалярное произведение векторов, но лоб получается как-то слишком сложно. В примере с пространственным манипулятором для координаты x,z имеем "гребенку", чем она вызвана? Не жесткостью ли?

Просто шаг выбран достаточно крупным, да и не самая удачная траектория из бесконечного множества возможных.

Центр треугольной платформы плоского манипулятора(показаны две конструкции)
движется по заданной прямоугольной траектории.Поскольку механизм имеет 2 степени
свободы,то использовалась, предложенная А.Б. Ивановым, процедура
анимации механизмов с несколькими степенями свободы.

---

RPRrestangle.smz (9 KiB) downloaded 111 time(s).

Расскажу как можно использовать метод в linux. Во-первых есть замечательный smath, который считает и численно, и символьно. Символьные вычисления можно делать и в maxima. Файлы имеют расширение wxm, каждый шаг выполняется по ctrl+ent. Осталось рунге и графика. Это делаю в octave. Файлы имеют расширение m, в версии 3.8 есть появился графический редактор, можно и через консоль достаточно дать адрес файла.

---

lin.zip (1 KiB) downloaded 86 time(s).

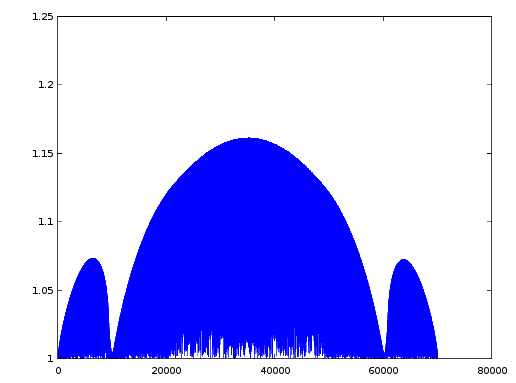
Теперь про гребенку. Я не понимал добавленного уравнения x1=0; или x6=0; Теперь я понял, что надо мысленно добавлять знак дифференциала, одно уравнение отдохнет, другое поработает и наоборот. Вот результаты при шаге 1е-3, 1е-4. Гребенка есть, пропорциональна шагу. Для определения точности сравним эти результаты. Теперь сделаем простую аппроксимацию, уменьшим кол-во точек в 2 раза: xi=(xi+x(i+1))/2, уменьшим шаг теперь не на порядок а в 2 раза, опять сравним. Результаты отличаются на порядок гребенки нет.

---

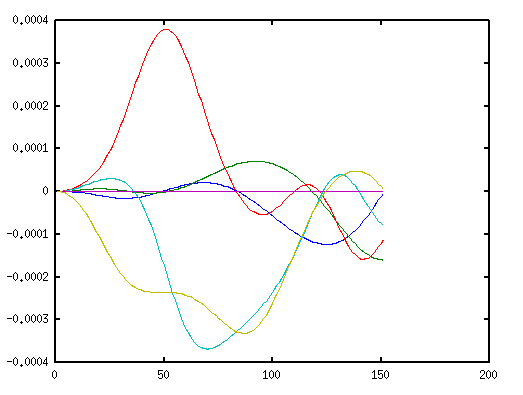
Сделаем анимацию точки центра окружности, x1 поменяется на x1+t. Не смог это сделать в octave, сделал в с++, но главное это скорость. 1е7 за 2 сек. К сожалению не знаю, как анимировать это, поэтому уменьшаю кол-во до 5е5 и скармливаю octave.

---

3.avi (809 KiB) downloaded 94 time(s).

“Гребёнка” появляется от буквального понимания количества степеней свободы. Другими словами, мы стараемся не столько показать реальную траекторию точек механизма, сколько получить решение недоопределённой системы нелинейных уравнений, которая является математической моделью механизма. Сколько степеней свободы у механизма бы ни было, они все одновременно не используются. Просто чем больше степеней свободы, тем больше вариантов траекторий. Траектории же можно задавать добавлением в исходную систему уравнений, а не только выбирать из всех возможных с помощью “ступенек”.
Что касается анимации, то, например, тот же Maple реализован на C, тогда зачем выполнять работы в C, когда Maple практически всё сам делает за человека – человеку остаётся только фантазировать.

https://vk.com/doc242471809_380217387
https://vk.com/doc242471809_378352452
https://vk.com/doc242471809_379935473

Алексей, Ваши анимации как симуляции, потрясающие. У меня есть цель освоение с. Ber7 сделал анимацию, выбирая шаг по какому-то алгоритму. В определителях содержатся сомножители x1 и x6 соответственно. Я просто возьму и буду в цикле и буду поочередно умножать первую систему на cos(20*i/N), вторую на .5 +.5*sin(i*N), i-шаг, N=5e5. Приведу длины для проверки. Кстати можно ли говорить о вероятной траектории?

---

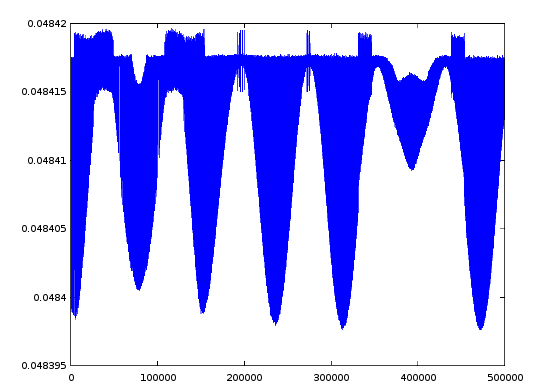
Могу подтвердить, что коль у Вас нет начально определённой траектории, то она будет вероятностной при степенях свободы от двух и выше.

Замечание к #13. Показаны квадраты длин. Попробуем расширить пример из #11. Длины 2.5 и 2.5. Начальные координаты {-1,0,.5,2,2,0}. Интересно увеличение радиуса окружности, на картинке показаны координата по y, большая единицы для крайней левой точки.

---

grelkn, я не понял выражения "Замечание к #13" и "пример из #11".Приложите,
пожалуйста,файл с Вашими проверками,возможно, будет понятнее.

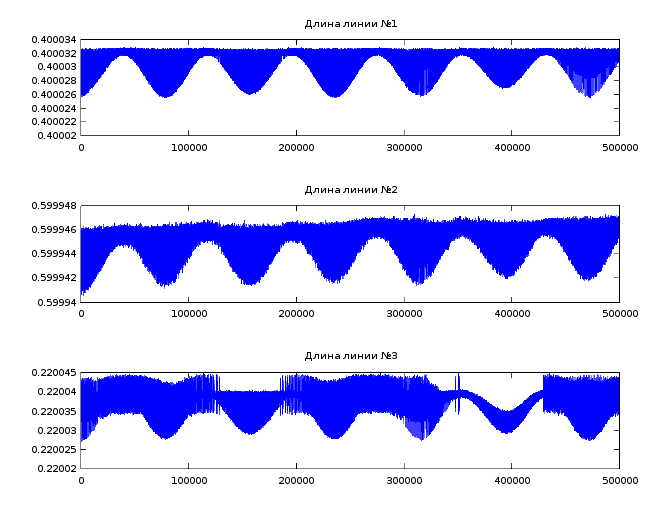
Числа 13 и 11 это номера записей от 7.04 22:35 и от 3.04 21:50. Система из 11 записи получена модификацией плоского трехзвенного манипулятора1 из 2-ой. Начальные точки {.0361,.3984,.5334,.734,.5142,.9532}. Четвертое уравнение изменено на x[5]*x[5]/.64+(x[6]-.65)*(x[6]-.65)/.3=0.7195. Прилагаю "новую" анимацию и проверку длин.

---

Для поддержания интереса к степеням свободы. Шесть степеней свободы твёрдого тела.
https://vk.com/doc242471809_383336706

Рабочий орган манипулятора перемещается от одной позиции обработки детали к другой.
1.По прямолинейным траекториям

2.По аппроксимирующей кривой

---

Line.pdf (177 KiB) downloaded 90 time(s).

К сообщению №19. Пример во многом демонстрационный. Задачу можно решить легче. Сделать цикл в цикле. Во внутреннем число шагов определяет длину, во внешнем меняем коэффициент. Тем не менее показано, что все параметры можно сделать изменяемыми при каждом шаге. В книге Артоболевского "Механизмы в современной технике" приведено много механизмов, различающихся положением центра окружности и начальными координатами. Если распараллелить выполнение метода, то можно изучить вопрос устойчивости выбранной характеристики. Например не только находить точки, которые движутся по прямой, но и определить диапазон с устраиваемой погрешностью.