Вращение с одновременным уменьшением длин сторон
многоугольников.Траектории вершин образуют логарифмические
спирали.Идея взята с сайта http://mathworld.wolfram.com/Whirl.html

---

Wolfram1.smz (3 KiB) downloaded 285 time(s).

Новогоднее
]

---

Happy.sm (7 KiB) downloaded 280 time(s).

Оптическая иллюзия
Идея взята с сайта
http://www.mapleprimes.com/maplesoftblog/35171-Its-Better-With-Maple
Хотя расстояние по вертикали между кривыми постоянно,
кажется,что при удалении от оси Y ,они становятся ближе.
Анимация позволяет преодолеть оптическую иллюзию

---

Illusion.sm (5 KiB) downloaded 288 time(s).

Качение диска по параболе

---

ParCyc.smz (4 KiB) downloaded 288 time(s).

ViewerFileType в анимации
https://smath.com/wiki/GetFile.aspx?File=InterAnim.rar

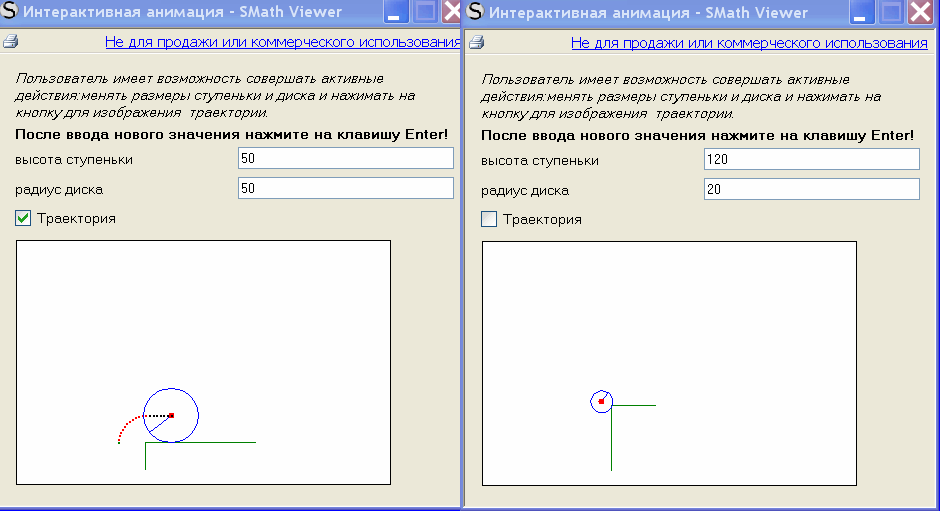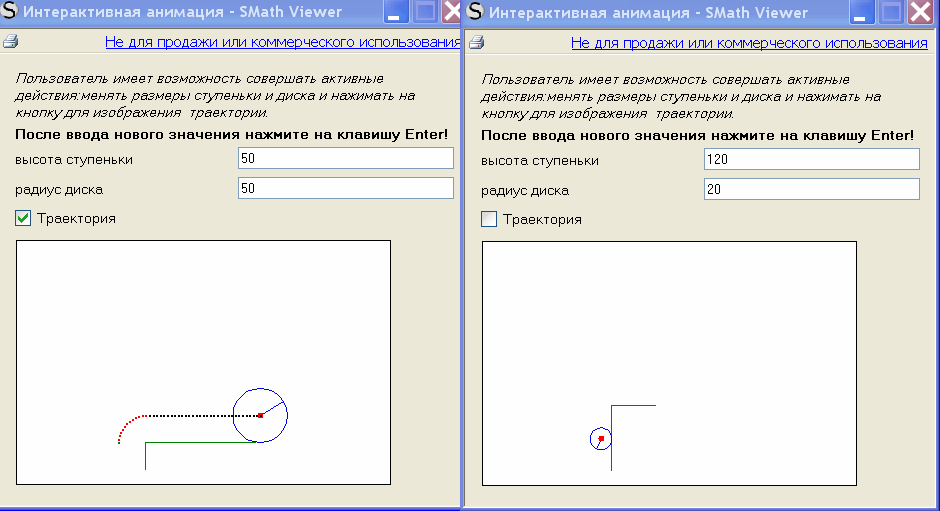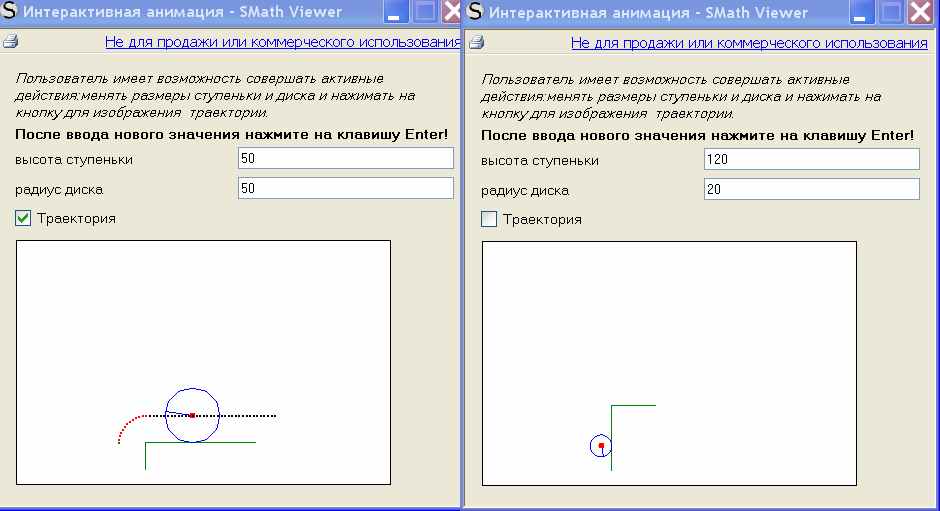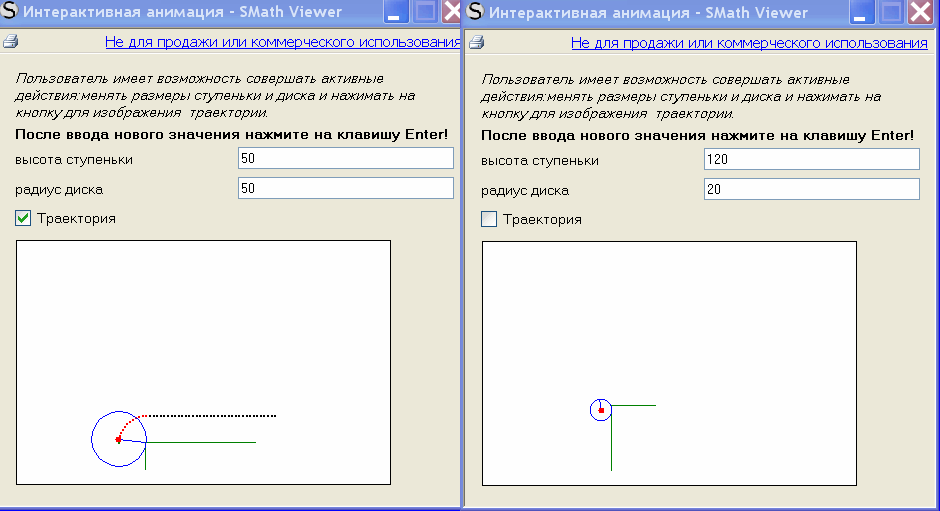
Интерактивные возможности ЕХЕ файлов,созданных вивьером ,позволяют
пользователю активно влиять на анимационную картинку. В примере использовано
приложение CheckBox
http://en.smath.info/forum/resource.ashx?a=1458

---

Задачи Леонардо Да Винчи на разрезание и складывание фигур

---

Leo2.smz (5 KiB) downloaded 261 time(s).

Перенос трехмерного изображения на двумерный(плоский)
график методом проф.А.Б.Иванова.
1По матрице из трех столбцов(x,y,z) строим 3d график и выбираем нужный ракурс;
2.С помощью линейного преобразования координат поворачиваем
все точки матрицы на угол (углы),соответствующий ракурсу и получаем новую
матрицу
3.Из трех столбцов новой матрицы выбираем два и подставляем в 2d график
Показана анимация двух поверхностей: первая построена А.Ивашевым,вторая
В.Мезенцевым(Уни).Анимация выполнена на плоских графиках.

---

But1.smz (5 KiB) downloaded 271 time(s).

Обновлено.Исправил ошибку в первой матрице
преобразования координат.

---

TorSphere.smz (5 KiB) downloaded 269 time(s).

1.Кручение и изгиб пластинки
2.Кручение и изгиб панели

---

Plate.smz (6 KiB) downloaded 257 time(s).

Работа классического варианта метода Драгилева на примере системы двух нелинейных уравнений:
(4*(x1^2+x2-11))*x1+2*x1+2*x2^2-14+cos(x1)=0;
2*x1^2+2*x2-22+(4*(x1+x2^2-7))*x2-sin(x2)=0;
Для одного начального приближения (-1,1,1) переменных x1,x2 и постоянного начального значения для вспомогательной переменной находятся все 9 решений системы на плоскости (в пространстве R^2) через 3d (пространство R^(2+1)) .
https://vk.com/doc242471809_392966449
Выполнено в Maple, текст программы можно посмотреть по ссылке
http://www.mapleprimes.com/posts/200585-Draghilevs-Method-Fx0-Animation

Анимация качения без проскальзывания с дополнительной степенью свободы. Если совсем по-простому, то качение по кривой, когда центр колеса принадлежит плоскости, перпендикулярной к кривой.
https://vk.com/doc242471809_389197688
https://vk.com/doc242471809_392866881
https://vk.com/doc242471809_393738754