Dear All,

I have got a question / request for help regarding Bessel functions:

First: Is there any plugin or function in SMath Studio for Bessel functions?
(Maybe not, at least I didn't find such a thing anywhere.

My problem now is that I need to calculate some heat transfer problems using Bessel functions as
trancendent equations for cylindrical bodies.

After a short while I found out that Bessel functions are really hard to compute due to the maximum available number range. (It is a general problem since there are very high numbers & very small numbers to compute at the same time).

A lot of much more clever people than me have found ways to approximatley decribe the Bessel functions in a more "computer-friendly" way by using ploynoms for example.
A very good solution I have found is from John Harris, Intel. So I decided to use his approach.
(see attachment). It is working very well so far, but now I want to increase the precision a liitle bit by adding one or 2 summands to his P and Q polynoms (see attachment) But unfortunately I don't fully understand his notation form not even though he is describing it. (sse attachment)


Is there anybody who could help me with that?

Later I will contribute the calculation of non-stady state heat transfer problems, acc. the boundary conditions of the third kind for simple bodies like plate, cylinder, and sphere.

Thank you veryvery much in advance. (The problem is described in the attachment very clearly.)


AlphaBeta

---

Bessel Computation for Heat Transfer Cylinder.sm (573 KiB) downloaded 172 time(s).

Try this. I just literally defined the functions and it seems to work.

---

Dear mKraska,

you have saved my day. Thank you very very much.

Now I also can understand the notation. I really got stuck here before.

My goal is to have functions for calculating:

a)Plate: wall temperature, middle temperature and tranferred Q
b)Cylinder: wall temperature, middle temperature and tranferred Q
c)Sphere: Cylinder: wall temperature, middle temperature and tranferred Q

as SMath Studio functions, where you can solve for either the Fourier Number,Biot Number or one of the parameters above
based on the publication of Prof. Grigull. For the plate it works well already.

When I am finished with it I will contribute it to the community.

Again, thank you very, very much for your competent and also lightning fast reply.

Hello,

Wrote

First: Is there any plugin or function in SMath Studio for Bessel functions?
(Maybe not, at least I didn't find such a thing anywhere.

Yes, there is a plugin which includes those special functions (Bessel, Modified Bessel, Integral functions etc.). Mathcad EFI made by uni. I was using them in my teaching few times. Unfortunately, the plugin is not working with the most recent SMath version. I hope that uni will find the way to recompile and put it in the Online Gallery, or expand the existing Alglib in order to include Bessel functions as well.

Regards,
Radovan

Wrote

Hello,

Wrote

First: Is there any plugin or function in SMath Studio for Bessel functions?
(Maybe not, at least I didn't find such a thing anywhere.

Yes, there is a plugin which includes those special functions (Bessel, Modified Bessel, Integral functions etc.). Mathcad EFI made by uni. I was using them in my teaching few times. Unfortunately, the plugin is not working with the most recent SMath version. I hope that uni will find the way to recompile and put it in the Online Gallery, or expand the existing Alglib in order to include Bessel functions as well.

Regards,
Radovan

Done. You must manually copy the mathlib.dll to the userefi folder (".../Application Data/.../91a20d24-c30b-4774-9b1b-4d502a80420f/x.x.x.x/userefi/" ).

---

mathlib.sm (59 KiB) downloaded 127 time(s).

Thank you uni

It seems I had a lucky guess this time. I've seen the EFI plugin in the Gallery. Installed it first and then copied the mathlib.dll in the place you mentioned. Bessel and other functions are back . Here is the result using the file by AlphaBeta. By the way, this much faster than using the approximation formulae.

[albumimg]210[/albumimg][albumimg]211[/albumimg]

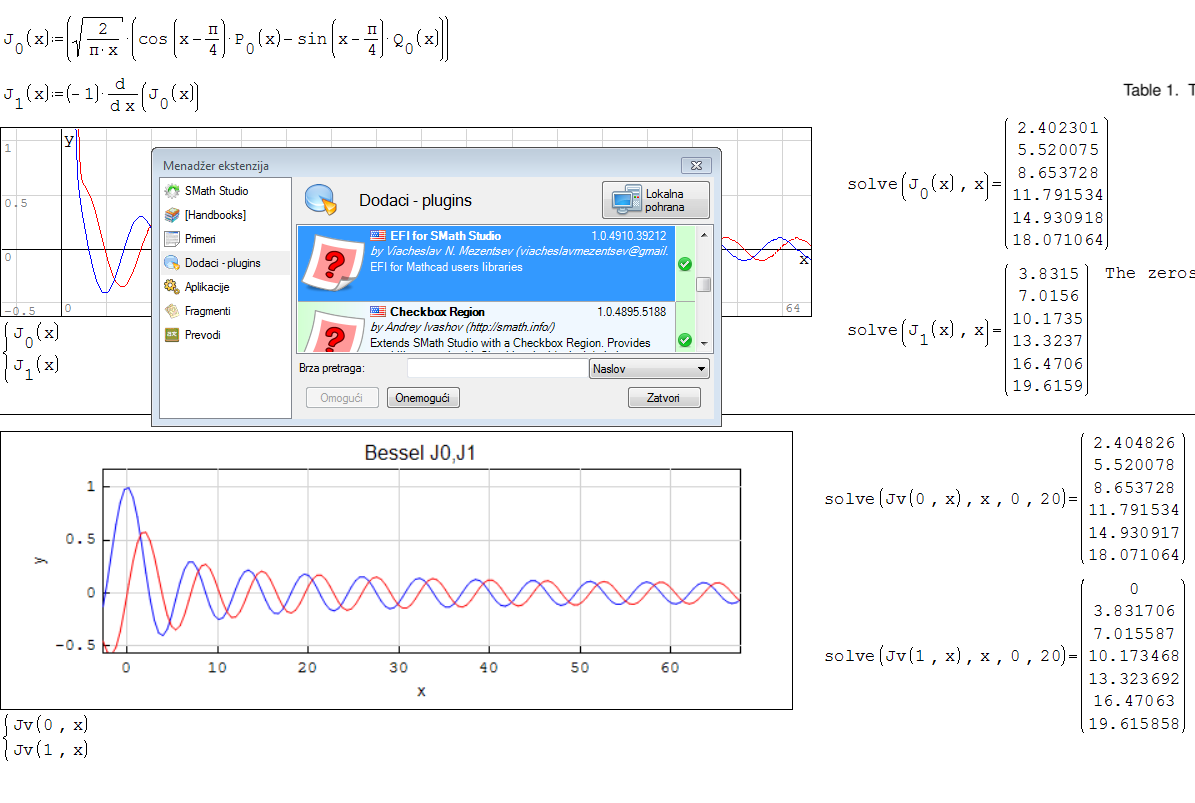
Huh...this was a bit complicated

It appeared that the more complicated become to follow the functions, their plugins etc. Once more to say, that there must be a way to see where the functions came from. Again, "all" category become overcrowded. Is there any way that for one of the next release the function category be devided into the external plugins and their accompanied functions?

Regards,
Radovan

error when loading SMath: OKAWSP6.dll was not found

Wrote

error when loading SMath: OKAWSP6.dll was not found

This is because that you have unpacked the entire archive. Do not use wspmcad.dll (Water Steam Pro).

ok done but afterwards i've tried the sample with the last mono version, it says "function is not defined" for In and Jn functions

Wrote

ok done but afterwards i've tried the sample with the last mono version, it says "function is not defined" for In and Jn functions

Did you mean on Bessel functions by In,Jn ? Their names are actually Iv, Jv.

it may not have importance. I haven't looked well the sample. See this video:
http://screencast-o-matic.com/watch/cI1XqFVwTX

Originally the library (and demo) was intended for Mathcad, where such functions are present.
It is strange that it works in Linux. I thought this plugin in Linux will not work.

uni, it is not linux but windows, running the mono build

Hi Folks,

thank you very for yor replies.
I will download the plugin as soon as possible. It will make my life easier.

But nevertheless attached you can find my "home-brew"-approach towards the Bessel function.
Actually I only wanted to solve a heat transfer problem.

Now I am a litte bit

Also thanks to M. Kraska.

Best regards

---

20130612 Bessel Modified.sm (1023 KiB) downloaded 97 time(s).

Hello,

The results from solve() depends on the equation, range and decimal places (Tools|Options|Calculation Decimal places). See the result if you change the equation, give different range and set 15 decimal places.

[albumimg]216[/albumimg]

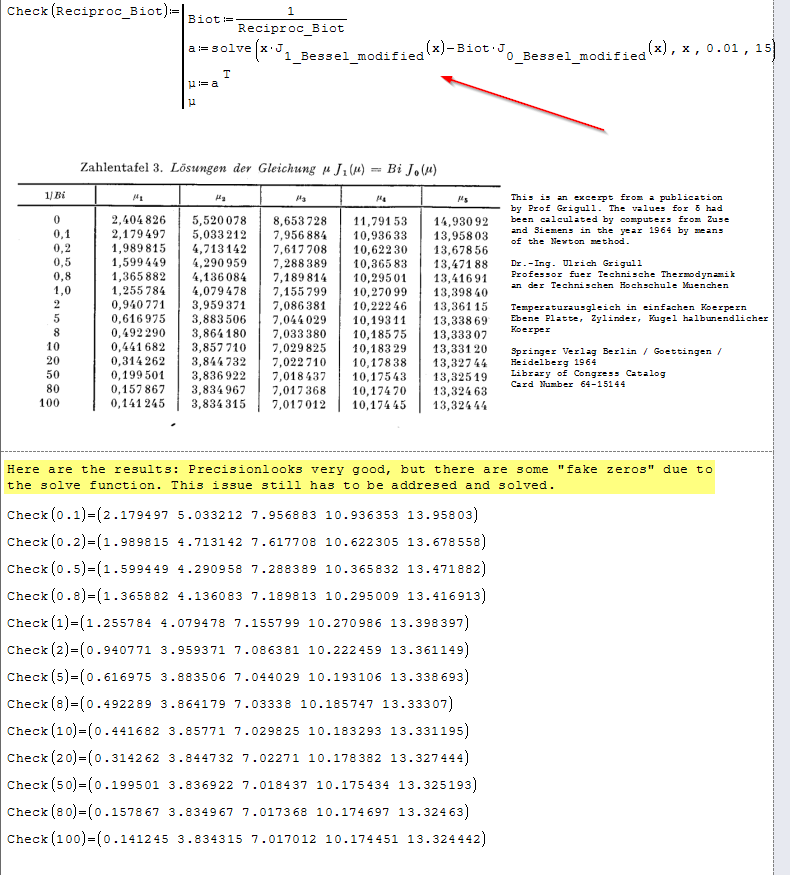
Regards,
Radovan

Hello Radovan,

thank you for your hint. I know that the solve function will produce some "ghost-zeros" in certain cases depending on the function, the range and the precision. I have sorted this out before by means of a little program within SMath using BiSection or NewtonRaphson, or using the initial zeros and then making a second, more refined "solve"-run using closer ranges. Additional knowledge about the functions periodicy is also helpful here.

Yesterday I was happy that it at least does work in principal now. ( The last Bessel function I have seen was 25 years ago)

But generally spoken, wouldn't it be a dream to have a clever solve algorithm which does such things automatically?
(I know that trying this is absolutely no simple endeavor. Multiple strategies and various algorithms would have to be employed depending on the current situation at hand...)

I have one idea - it might be stupid one - (please consider that I am at no means a professional here):

1.Every plot is a kind of a approximation, means, when you plot it you can "see" the zeros since the calcilated points are connected with a line

2.If one would have kind of a "pre-parser" actually "seeing" these crossings between the function and x-axis an then this parser would remember the area. Image you go along the x-achsis with a loupe. You can adjust the magnification, the loupe has a certain diameter which would represent the "alarm" range.

3. After the "parser" has found and remembered the interesting areas some more analytical function could be applied in these areas then

Okay, just a dream...
By the way, increasing the precision in the program setting did not improve the situation.
But of course narrowing the range does remedy the situation. But such things need to be done "manually" and with knowledge about the function.
Or can be automatized by means of an algorithm for solving a very specific problem, but not in general.

Best regards
Dirk

Hello Dirk,

Wrote

But generally spoken, wouldn't it be a dream to have a clever solve algorithm which does such things automatically?
(I know that trying this is absolutely no simple endeavor. Multiple strategies and various algorithms would have to be employed depending on the current situation at hand...)

Andrey made solve() and, as he said, it uses some kind of searching algorithm - do not know which one. If you know any algorithm of this kind, or can find some pseudocode on the Net, you can let Davide Carpi know about this (he is developing NonlinearSolver plugin). He alredy made some of "my dreams come true" regarding nonlinear solvers in SMath.

Regards,
Radovan

Wrote

But generally spoken, wouldn't it be a dream to have a clever solve algorithm which does such things automatically?

Stay tuned for the new NonlinearSolver, I think Davide "might be" preparing something.

Hello,

I already have played around a little bit with the nononlinear solvers. NewtonRaphson and Bisection I like best. Unfortunately I don't know any sophisticated solver algorithm beside the standard ones.(25 years ago I had made an amateurish Newton method solver on a Sinclair Spectrum and I still remember how hard it had been when the darn thing would not converge :-).
The package is very nice. I have read how much you appreciated it. A little bit more of documentation would be good. But reading the examples in the forum is also good. So keep on posting and share your examples and ideas.

Actually the built- in solver "solve ( function, variable, start range, end range)" is not so bad for most of the basic tasks. What I like is that it returns multiple zeros in a given range and that it is quite fast. Maybe it just needs a little bit tuning? But it is not so optimal that it sometimes returns ghost zeros, and you really need a plot so you can differentiate between the " true" and the " false" ones. But I found out that most of the false ones will result in a quite huge deviation from zero when put back into the equation. This would be a kind of a cross check which I think could be easily implemented into the algorithm. Most surly I will stay tuned. In the meantime don't calculate important parts of aircrafts our rockets relying on the current solve function without having had a second look.

The last sentence was a joke! :-) Not criticism!