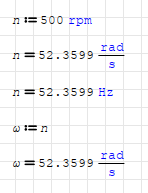Hi,

I've seen a few threads on this forum discussing the confusion with rpm unit. I'm not going to claim that this unit has wrong definition in SMath since it looks like it's just defined differently than one might expect. Anyway, can you tell me how to convert rotational speed in rpm to angular velocity in rad/s without having to get rid of units in the whole document ? I need a correct value of angular velocity for further calculations.

Here's what I get in SMath:



And here's what I expect (result from Wolfram Alpha):



It seems that I can't use built-in unit conversion in this case. So what's the best workaround ? Is it necessary to redefine the unit or maybe I can do something else to make it work ?

Thanks in advance for your help.

As you can see, Smath already stores "n" in Hz.
If you intend to convert manually then you have to do it correctly as shown here:

sergio

Thanks, it seems to work:



Is that the only possible workaround apart from not using units ?

Units can be ignored by a contextual menu
UnitaSilenziate.sm (2 KiB) downloaded 27 time(s).
sergio

I don't get why you multiply n with something else.
n is already in rad/s. Just assigning n to w should be enough.
I just walk/run 7 km, maybe my brain can't comprehend everything right now.
Am I missing something here?

Regards

Hi,
rpm is obviously wrongly defined in SMath.
The unit is revolutions per minute, not 2pi per minute.
Regards

Wrote

Hi,
rpm is obviously wrongly defined in SMath.
The unit is revolutions per minute, not 2pi per minute.
Regards

Nothing is wrong with rpm definition in smath, with respect to SI units.
According to SI and National Institute of Standards and Technology (NIST);
rpm is defined as revolution per minute, or rad/s, or (1047197xE-1 Hz).
One revolution is one round, which equals to 2π.
2π/60s = π/30s = 0.1407 Hz, it is clear.
Maybe you are taking r as round, round per minute.
Which equals to 1/min = min^-1.
But this is not a latest SI approach.
Usually senior imperial unit users do that I guess.

Here is an article of NIST about units.
You can see rpm definition in it, which is rad/s.
https://physics.nist.gov/cuu/pdf/sp811.pdf

Regards

SMath is wrong in that it displays angular velocity by default in Hz. Hz is not a unit for angular velocity but for frequency, meaning events per time. Whatever events are, for sure not an advane of 1 rad in angular position.

It would be better to at least display 1/s as a unit, which leaves it to the user to imply rad by 1.

It is also wrong that rpm is listed in the category "frequency" in the units selection dialog. Should be "angular velocity"

Both issues encourage the user to the wrong assumption that angular velocity is the same as frequency.

When I was studying Mechanical engineering I was told that the angular velocity is just approximately one tenth of the rpm.

Strictly speaking, they should have said that the angular velocity in rad/s is one tenth of the angular velocity in revolutions per minute. The combined conversion of revolutions to rad and minutes to seconds results in the factor of 1/10 with 5% error. You could use degrees per year or whatever, it still is an angular velocity, no matter what unit is used.

That's how it is in SMath Studio. An option would have been to explicitly say that revolutions per time is a frequency with the event being a full revolution. Then converting from frequency to angular velocity would require the factor of 2 pi as expected by a lot of users. Yet SMath Studio defines a revolution ('rev) not as an event but as an angle of 2 pi, which is not consistent to this understandig.

We are getting closer. A specification in rpm is simply a frequency. The tachometer in your car does not indicate angular velocity.

By the way, the NIST document above gives the conversion factor between the frequency in the unit rpm and the angular velocity in the unit rad/s.
It does not define rpm as rad/s.
rpm and rad/s are two different units.

to complete this:
The NIST document (https://physics.nist.gov/cuu/pdf/sp811.pdf) defines rpm in chapter 8.1 as (rotational) frequency:


At the top of page 54, you will find the table caption


and further down the conversion factor.


Try to harmonize this with the Smath definition...

It is quite possible that in older textbooks rpm is defined contrary to today's SI usage.
But a modern program should perhaps conform to the current SI standard?

(By the way, in Mathcad 15 it is also defined like in Smath. But this does not make it better).
regards, Johannes

Wrote

rpm and rad/s are two different units.

The glass is ½ full as well ½ empty.
Here, s is typical ... min, hr, day, year ...

Unit conversion may be challenging: https://en.wikipedia.org/wiki/Mars_Climate_Orbiter

Wrote

... A specification in rpm is simply a frequency. ...

Nope. You try to use the formula ω=2*π*n where ω is the angular speed and n the frequency. But rpm isn't an unit for frequency, it is the usual unit for angular speed, as reflected in the NIST document, where I don't think they got the dimensions wrong. BTW the NIST is only one country institute, and those who have the last word are the BIMP people, for whom rpm is not a valid unit due to the confusion it introduces, and they do not include it in their documentation.

If you want to write n = 5oo as frequency, you can use cps, cycles per second, which actually it's the old name for Hertz.

Wrote

...The tachometer in your car does not indicate angular velocity....

Yes, it does. As far I know, if I sense an engine rotating with a tachometer and read 3600 rpm it means 376.9911 rad/sec, which agrees with the SMath answer.



Best regards.
Alvaro.

Wrote

Unit conversion may be challenging

That's why it entertains this Forum so much.
My slide rules had no unit, neither my TI-58/59,
I won golden bridges with these last two.
Cheers, have a good day ... Jean

Wrote

The tachometer in your car does not indicate angular velocity.

Between the rpm sensor and the analog rpm indicator
there is a converter... rpm dial ± X %

Wrote

The tachometer in your car does not indicate angular velocity.

On the contrary of your statement, tachometer indicates the angular speed of a rotating shaft. Maybe you meant speedometer.
https://www.britannica.com/technology/tachometer

Razonar is right, rpm is not a unit of SI nor it is a derived unit. It is commonly used because it is easier to comprehend.
rpm is not in SI, hence revolution is not a unit. It can not be shown with base SI units. And [1/s or 1/min] is not recommended to use as angular velocity.
Quantities called “frequency”, “angular frequency”, and “angular velocity” always be given explicit units of Hz or rad/s and not s−1. (Page 26)
https://www.bipm.org/documents/20126/41483022/SI-Brochure-9-EN.pdf

You shouldn't distort the meaning of SI documents. NIST conversion table shows 1 rpm (r/min) = 0.1407 rad/s.
Conversion is for numerical parts, NOT units. And I guess it is in NIST just for conversion purpose only.
You can check with every conversion tool, nearly all of them shall tell you 1 rpm = 2π/60s.

Wrote

It is quite possible that in older textbooks rpm is defined contrary to today's SI usage.
But a modern program should perhaps conform to the current SI standard?

Current SI standard is being obeyed by SMath, and Mathcad too.
We have shown you the NIST SI documents, BIPM SI documents, examples, etc.
rpm is already defined correctly in SMath. There is no need to continue this debate.

Regards

Wrote

Unit conversion may be challenging:

It is and it is more from a dead horse.
Plug my frequency meter in the grid ► 60 Hz, i.e: frequency
However, not from Smath !

Wrote

Unit conversion may be challenging: https://en.wikipedia.org/wiki/Mars_Climate_Orbiter

The problem was not conversion, literally.
Because Lockheed didn't converted imperial units to SI.

Regards.

Wrote

Nothing is wrong with rpm definition in smath, with respect to SI units.
According to SI and National Institute of Standards and Technology (NIST);
rpm is defined as revolution per minute, or rad/s, or (1047197xE-1 Hz).

Overlord, you've misread the NIST conversion table. As listed on page 54 and again on page 67 at https://physics.nist.gov/cuu/pdf/sp811.pdf:

The table says:

Quote

To convert from:

rpm

To

rad/s

Multiply by

1.047198E−01

Note that the NIST table does not convert rpm to Hz, it converts rpm to rad/s. I've laid out the calculations to prove it below:



Therefore:


Or, using angular frequency, the NIST value is calculated:


The easy way to tell if the calculation is right is by using the relation between frequency (f [Hz]) and angular frequency (ω [rad/s]):


In other words, the angular frequency (in rad/s) is 2 pi times greater than the frequency (in Hz).

SMath erronously reports:


The correct conversions should therefore be:


The SI Brochure (9ed) specifically warns against making this kind of error (Page #140 (page 26 of the PDF))

Quote

It is especially important to carefully distinguish frequencies from angular frequencies, because by definition their numerical values differ by a factor of 2π. Ignoring this fact may cause an error of 2π. Note that in some countries, frequency values are conventionally expressed using “cycle/s” or “cps” instead of the SI unit Hz, although "cycle" and "cps" are not units in the SI. Note also that it is common, although not recommended, to use the term frequency for quantities expressed in rad/s. Because of this, it is recommended that quantities called “frequency”, “angular frequency”, and “angular velocity” always be given explicit units of Hz or rad/s and not s−1.

IMPORTANT NOTE: That last line: "... explicit units of Hz or rad/s..." is NOT equating Hz and rad/s (i.e. 1 Hz = 1 rad/s). It is saying that a person needs to SPECIFY whether they are using frequency (Hz) OR angular frequency (rad/s), especially since both of these "frequencies" can be represented with units 1/s, since radians are dimensionless:



QED.

You are totally right. rpm ► Hz is like a meter is so long.
If you are using a recent Smath version, quite a pity.
1983, I was consulting in-situ for Syncrude.
My TI-58 had no units.
Take care ... Jean