1 Pages (3 items)
Maxima weak solver - Maxima weak solver - Messages
#1 Posted: 4/7/2016 2:16:23 AM
#2 Posted: 4/7/2016 3:27:08 AM
Just a side note (unfortunately, unhelpful).
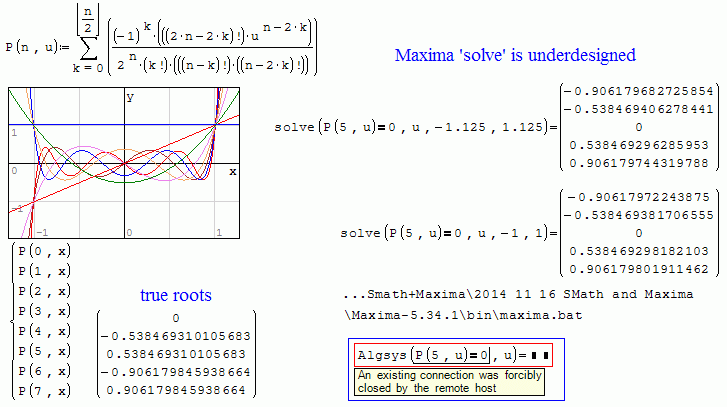
You keep using word "Maxima" in many places where it apparently doesn't apply (another example is here: http://en.smath.info/forum/yaf_postst7424_Maxima-X-Y-plot.aspx).
It looks like you mean that standard "solve" (all small letters) is a Maxima function. No, it is not, it is SMath own in-built solve().
In another post, you write:
Looks like you suppose that SMath itself is just a "shell" (interface) to its plugins. Well, that's not strictly true, these 2MB include its own load of math
Edit: maybe you'll find nonlinear solvers plugin useful?
It gives correct answers, though by carefully selecting ranges; you may directly control output precision.
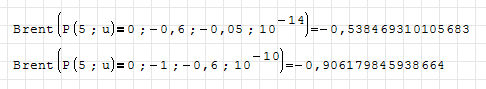
You keep using word "Maxima" in many places where it apparently doesn't apply (another example is here: http://en.smath.info/forum/yaf_postst7424_Maxima-X-Y-plot.aspx).
It looks like you mean that standard "solve" (all small letters) is a Maxima function. No, it is not, it is SMath own in-built solve().
In another post, you write:
WroteWhat I understand from Smath Studio: it is a stand alone big tool, a math tool.
2MB user interface working from associated plugins [total size 5346 = 235 MB].
Looks like you suppose that SMath itself is just a "shell" (interface) to its plugins. Well, that's not strictly true, these 2MB include its own load of math
Edit: maybe you'll find nonlinear solvers plugin useful?
It gives correct answers, though by carefully selecting ranges; you may directly control output precision.
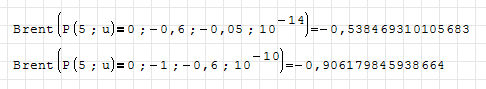
С уважением,
Михаил Каганский
1 users liked this post
Andrey Ivashov 4/7/2016 4:27:00 AM
#3 Posted: 4/7/2016 10:35:28 AM
Thanks Mike for Brent, I know about that stuff [Ref: Mathcad 11]
A much better candidate is the universal "Polyroots".
My remark cautionned Smath users about inaccuracy of "solve".
Brent("1:function", "2:condition", "3:condition", "4:condition")
- Brent's root-finding method of function "1:function", giving a
couple of delimiters "2:condition" and "3:condition";
calculation have at least "4:condition" function precision.
Jean
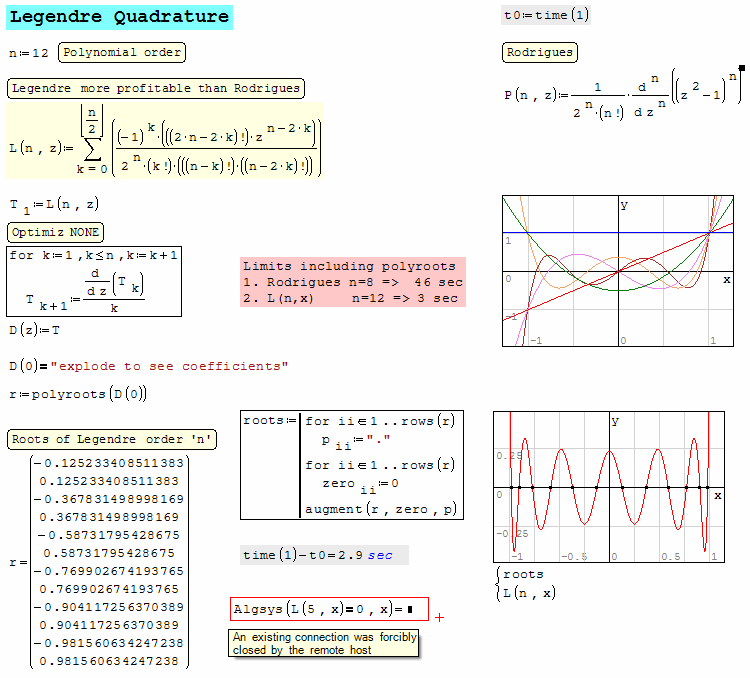
Integrate Quadratures Legendre Polyroots.sm (23.73 KiB) downloaded 733 time(s).
A much better candidate is the universal "Polyroots".
My remark cautionned Smath users about inaccuracy of "solve".
Brent("1:function", "2:condition", "3:condition", "4:condition")
- Brent's root-finding method of function "1:function", giving a
couple of delimiters "2:condition" and "3:condition";
calculation have at least "4:condition" function precision.
Jean

Integrate Quadratures Legendre Polyroots.sm (23.73 KiB) downloaded 733 time(s).
1 Pages (3 items)
- New Posts
- No New Posts