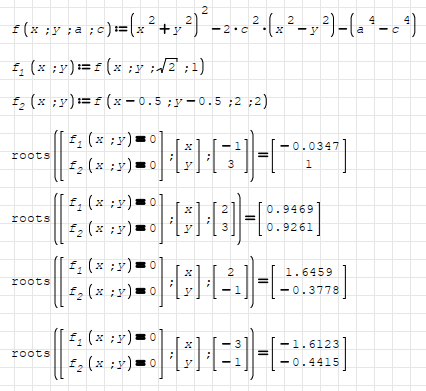1 Pages (11 items)
Newton method - Messages
#1 Posted: 4/8/2023 4:07:23 PM
I cannot use the roots function and must use one old good simple method by Newton.
What can you say about it?
Newton-Eng.docx (1.07 MiB) downloaded 587 time(s).
What can you say about it?
Newton-Eng.docx (1.07 MiB) downloaded 587 time(s).
1 users liked this post
Martin Kraska 4/9/2023 8:50:00 AM
#2 Posted: 4/9/2023 8:56:19 AM
Very nice.
I had problems when reproducing your 2D version. Depending on initial guess I got errors "requested matrix element does not exist". The situation seemed to improve a little by pre-allocating the vectors X and Y yet it didn't become really robust.
So instead of assigning to j+1 elements I used augment() to add new points to the iteration history.
This is the original version:
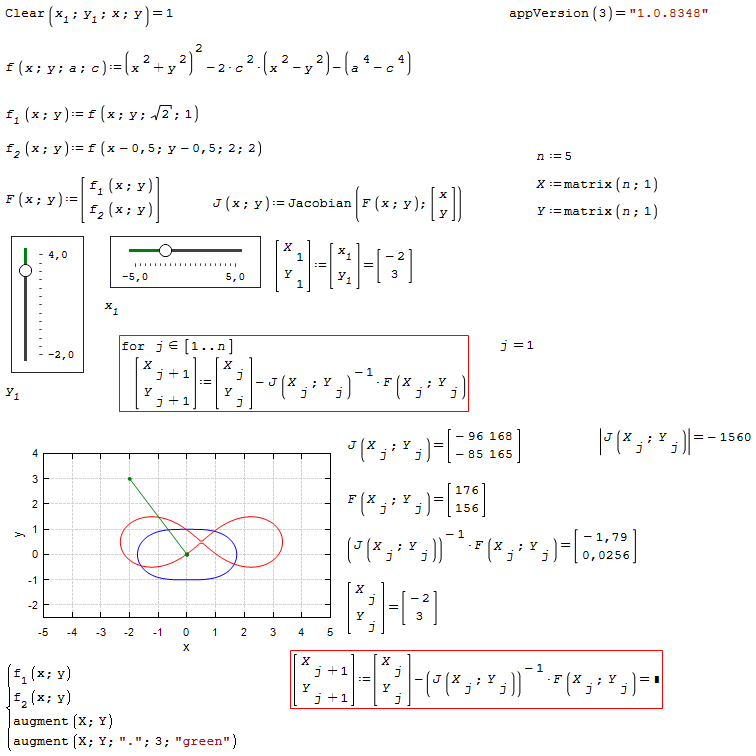
Newton2D.sm (21.4 KiB) downloaded 994 time(s).
And this is the modified version.
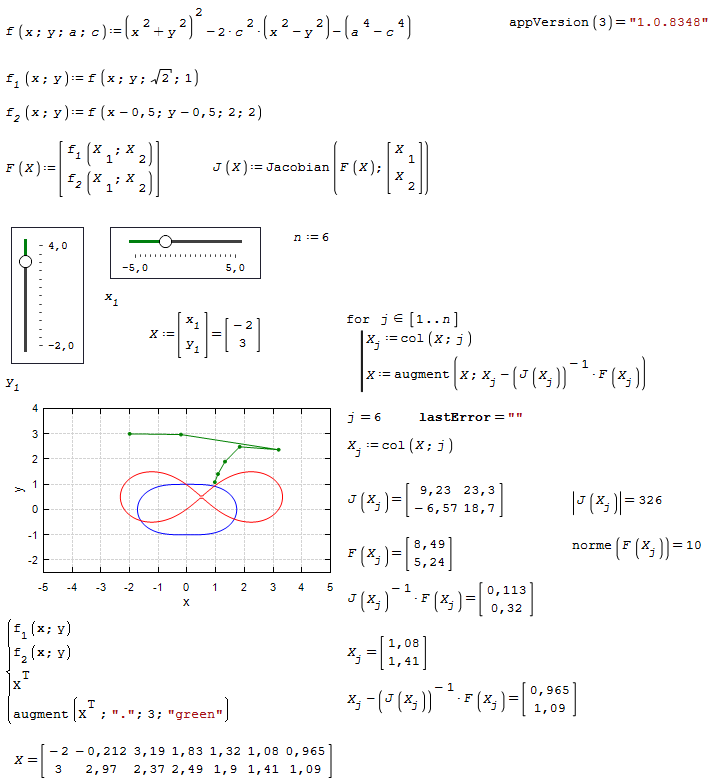
Newton2Da.sm (19.03 KiB) downloaded 1101 time(s).
I had problems when reproducing your 2D version. Depending on initial guess I got errors "requested matrix element does not exist". The situation seemed to improve a little by pre-allocating the vectors X and Y yet it didn't become really robust.
So instead of assigning to j+1 elements I used augment() to add new points to the iteration history.
This is the original version:

Newton2D.sm (21.4 KiB) downloaded 994 time(s).
And this is the modified version.

Newton2Da.sm (19.03 KiB) downloaded 1101 time(s).
Technische Mechanik mit SMath Studio: https://link.springer.com/book/10.1007/978-3-658-50592-9
#3 Posted: 4/9/2023 2:27:18 PM
Wrote... can't find 2nd root
2nd root confirmed exact.
Solve(f,q,x0,x1,TOL) Copy.sm (162.62 KiB) downloaded 1053 time(s).
#4 Posted: 4/9/2023 2:33:35 PM
#5 Posted: 4/9/2023 6:19:38 PM
Another way, keeping the mathematical formulation and the iteration algorithm separate. As here.
Newton2Da.sm (13.34 KiB) downloaded 1156 time(s).

Best regards.
Alvaro.
Newton2Da.sm (13.34 KiB) downloaded 1156 time(s).

Best regards.
Alvaro.
#6 Posted: 4/10/2023 12:25:58 PM
Thanks Alvaro, added to my next Samples visit.
Take care ... Jean
Take care ... Jean
#7 Posted: 4/10/2023 4:21:38 PM
#8 Posted: 4/10/2023 8:29:31 PM
WroteI cannot use the roots function and must use one old good simple method by Newton.
What can you say about it?
An old vintage in Smath ... two examples.
Take care Valery ... Jean.
Solve_roost f1(x,y). f2(x,y).sm (27.42 KiB) downloaded 1091 time(s).
#9 Posted: 4/11/2023 2:21:16 PM
Two variations added.
Newton2Da. v2.sm (38.35 KiB) downloaded 1081 time(s).
Newton2Da. v2.pdf (152.11 KiB) downloaded 631 time(s).
Best regards.
Alvaro.
Newton2Da. v2.sm (38.35 KiB) downloaded 1081 time(s).
Newton2Da. v2.pdf (152.11 KiB) downloaded 631 time(s).
Best regards.
Alvaro.
1 users liked this post
sergio 5/3/2023 2:29:00 PM
#10 Posted: 5/3/2023 12:37:31 AM
WroteTwo variations added.
Newton2Da. v2.sm (38.35 KiB) downloaded 1081 time(s).
Newton2Da. v2.pdf (152.11 KiB) downloaded 631 time(s).
Best regards.
Alvaro.
From my future article
Если уравнений не два, а три, то матрица Якоби будет состоять из трёх строк и трёх столбцов. При этом графически отображать решение придётся не двумя кривыми, а тремя поверхностями на 3D-графике, причём их взаимное пересечение и будет отмечать решение (задание читателю).
Слабо!
1 users liked this post
Alvaro 5/3/2023 3:21:00 AM
#11 Posted: 5/3/2023 12:02:25 PM
You may find this Treasury useful/productive.
Solve(f,q,x0,x1,TOL) Copy.sm (300.16 KiB) downloaded 1064 time(s).
Solve(f,q,x0,x1,TOL) Copy.sm (300.16 KiB) downloaded 1064 time(s).
1 Pages (11 items)
- New Posts
- No New Posts