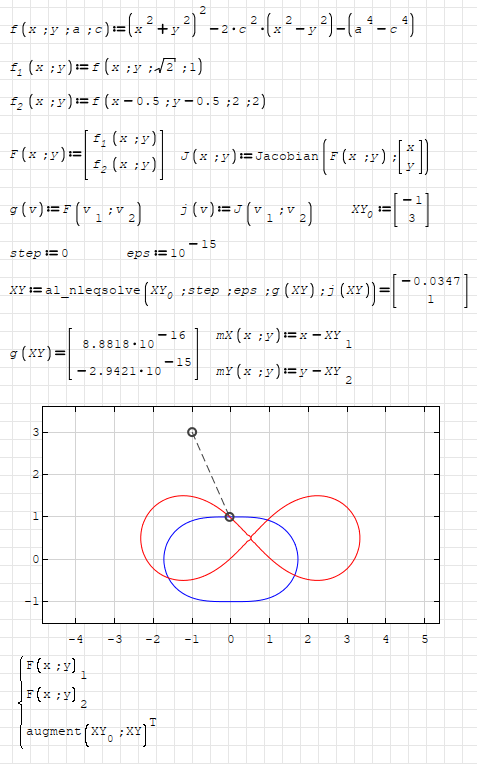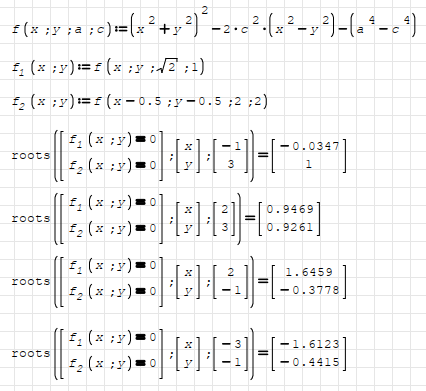1 страниц (11 вхождений)
Newton method - Сообщения
I cannot use the roots function and must use one old good simple method by Newton.
What can you say about it?
Newton-Eng.docx (1,07 МиБ) скачан 576 раз(а).
What can you say about it?
Newton-Eng.docx (1,07 МиБ) скачан 576 раз(а).
1 пользователям понравился этот пост
Martin Kraska 09.04.2023 08:50:00
Very nice.
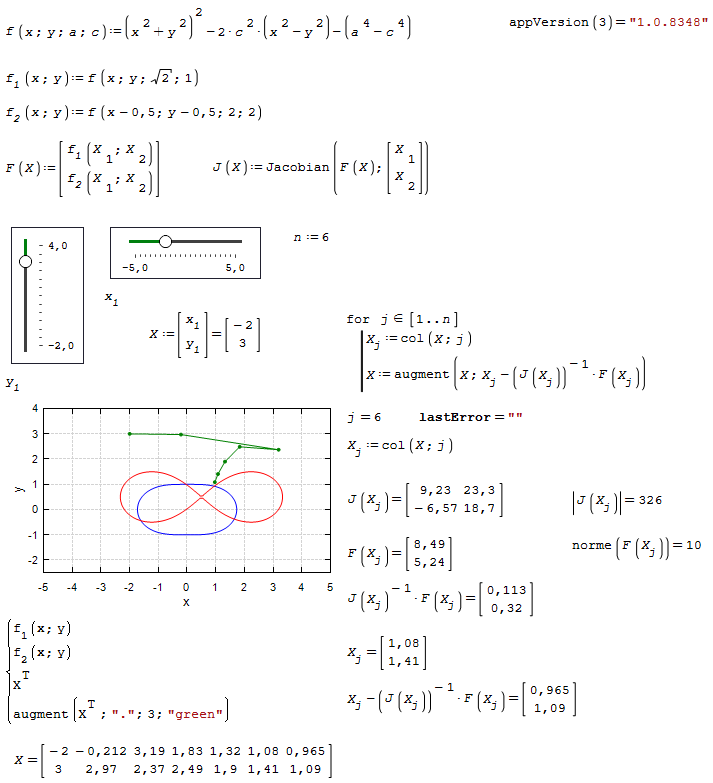
I had problems when reproducing your 2D version. Depending on initial guess I got errors "requested matrix element does not exist". The situation seemed to improve a little by pre-allocating the vectors X and Y yet it didn't become really robust.
So instead of assigning to j+1 elements I used augment() to add new points to the iteration history.
This is the original version:

Newton2D.sm (21,4 КиБ) скачан 977 раз(а).
And this is the modified version.
Newton2Da.sm (19,03 КиБ) скачан 1086 раз(а).
I had problems when reproducing your 2D version. Depending on initial guess I got errors "requested matrix element does not exist". The situation seemed to improve a little by pre-allocating the vectors X and Y yet it didn't become really robust.
So instead of assigning to j+1 elements I used augment() to add new points to the iteration history.
This is the original version:

Newton2D.sm (21,4 КиБ) скачан 977 раз(а).
And this is the modified version.

Newton2Da.sm (19,03 КиБ) скачан 1086 раз(а).
Technische Mechanik mit SMath Studio: https://link.springer.com/book/10.1007/978-3-658-50592-9
Wrote... can't find 2nd root
2nd root confirmed exact.
Solve(f,q,x0,x1,TOL) Copy.sm (162,62 КиБ) скачан 1031 раз(а).
Another way, keeping the mathematical formulation and the iteration algorithm separate. As here.
Newton2Da.sm (13,34 КиБ) скачан 1141 раз(а).
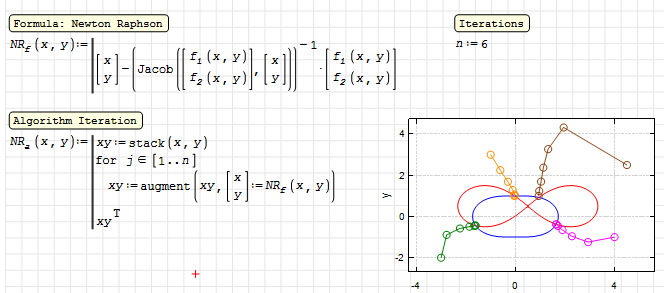
Best regards.
Alvaro.
Newton2Da.sm (13,34 КиБ) скачан 1141 раз(а).

Best regards.
Alvaro.
Thanks Alvaro, added to my next Samples visit.
Take care ... Jean
Take care ... Jean
WroteI cannot use the roots function and must use one old good simple method by Newton.
What can you say about it?
An old vintage in Smath ... two examples.
Take care Valery ... Jean.
Solve_roost f1(x,y). f2(x,y).sm (27,42 КиБ) скачан 1068 раз(а).
Two variations added.
Newton2Da. v2.sm (38,35 КиБ) скачан 1062 раз(а).
Newton2Da. v2.pdf (152,11 КиБ) скачан 620 раз(а).
Best regards.
Alvaro.
Newton2Da. v2.sm (38,35 КиБ) скачан 1062 раз(а).
Newton2Da. v2.pdf (152,11 КиБ) скачан 620 раз(а).
Best regards.
Alvaro.
1 пользователям понравился этот пост
sergio 03.05.2023 14:29:00
WroteTwo variations added.
Newton2Da. v2.sm (38,35 КиБ) скачан 1062 раз(а).
Newton2Da. v2.pdf (152,11 КиБ) скачан 620 раз(а).
Best regards.
Alvaro.
From my future article
Если уравнений не два, а три, то матрица Якоби будет состоять из трёх строк и трёх столбцов. При этом графически отображать решение придётся не двумя кривыми, а тремя поверхностями на 3D-графике, причём их взаимное пересечение и будет отмечать решение (задание читателю).
Слабо!
1 пользователям понравился этот пост
Alvaro 03.05.2023 03:21:00
You may find this Treasury useful/productive.
Solve(f,q,x0,x1,TOL) Copy.sm (300,16 КиБ) скачан 1046 раз(а).
Solve(f,q,x0,x1,TOL) Copy.sm (300,16 КиБ) скачан 1046 раз(а).
1 страниц (11 вхождений)
- Новые сообщения
- Нет новых сообщений