Can we create this in SMath?
Help me please.

This should be a good starter.

TBD:
- Parametrize the coordinates of point B.
- Add the missing members using vector algebra, no need for further equation solving.

Viergelenk.sm (40 КиБ) скачан 27 раз(а).

[RUS]В анимации пустые оси... Будем считать ее не только художественной, примем расстояния на осях X и Y равны друг другу в условных единицах. Получим решение при помощи метода Драгилева.
Красным цветом обозначены точки Т1..Т4, движения которых нужно установить. Голубым цветом обозначены точки с постоянными известными координатами C1, C2. Все координаты приближенно я получил в gimp.
Начальные условия: 4.10 -0.97 3.30 -3.22 2.35 -0.97 .69 -3.08
Точки константы: 3.75 -.97 2.7 -3.19
8-мь неизвестных, 7-мь уравнений. 5-ть уравнений получаются достаточно просто, 6-ое параметрическое, с 7-м непросто
Окружность С1, Т1
Линия Т1, Т2
Линия между Т3 и серединой Т1 и Т2
Линия Т2, Т4
Сумма длины линии Т2,С2 и длины линии Т4,С2
Параметрическое T3, первый участок xT3=const, yT3 меняется до некоторой известной величины
Теперь о последнем уравнении. Внимательно посмотрим анимацию. Видно, что точки 1 и 3 независимо друг от друга движутся с постоянной скоростью. Даже счетчик есть, где отношение 1:2.
Такая независимость возможна в случае если на k шаге покоится точка Т1, на k+1 шаге покоится точка Т3, то есть уравнение следующее:
p1(k)*xT1+p2(k)*xT3, где при p1(k)=0, p1(k)=1 и p1(k+1)=1, p1(k+1)=0
Не забываем о главном, о постоянстве скоростей Т1 и Т3. Поэтому делим всю правую часть на сумму скоростей Т1 и Т2/a. Коэффициент a постоянная величина, которая нужна чтобы т3 достигла заданной величины при β=90°
У меня получилась, что абсолютная скорость точки 3 превышает абсолютную скорость точки 1 где-то на одну треть.
Полную анимацию при изменении Т3 я выложу позже. В smath могу попробовать помочь повторить.

[ENG]There are empty axes in the animation... Let's consider it not only artistic, let's assume the distances on the X and Y axes are equal to each other in conventional units. Let's get the solution using Dragilev's method.
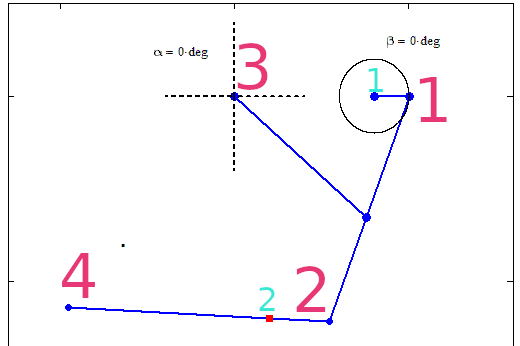
The red color denotes the points T1..T4, whose movements should be set. Blue color denotes points with constant known coordinates C1, C2. All coordinates are approximated in gimp.
Initial conditions: 4.10 -0.97 3.30 -3.22 2.35 -0.97 .69 -3.08
Constant points: 3.75 -.97 2.7 -3.19
8 unknowns, 7 equations. 5 of the equations are fairly easy, the 6th is parametric, the 7th is tricky
Circle C1, T1
Line T1, T2
The line between T3 and the center of T1 and T2.
Line T2, T4
Sum of the length of line T2,C2 and the length of line T4,C2
Parametric T3, first section xT3=const, yT3 varies to some known value
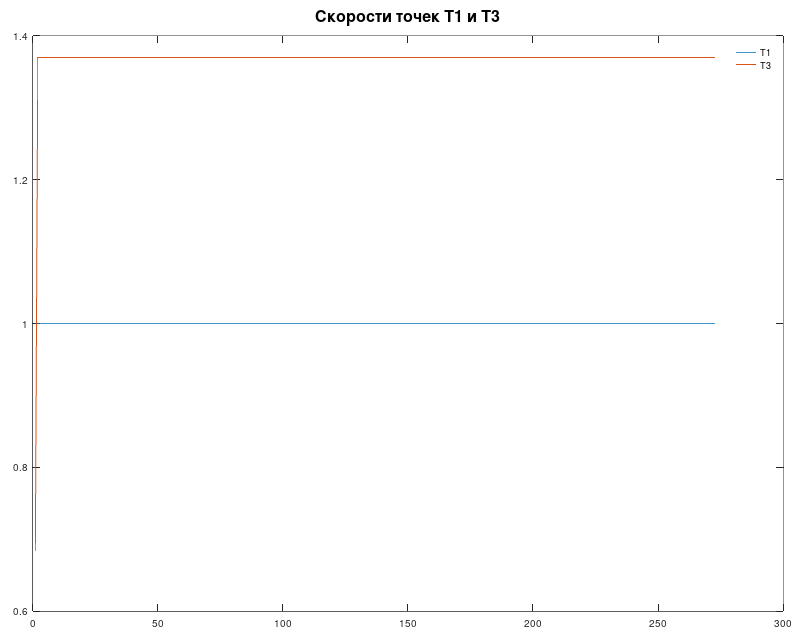
Now for the last equation. Let's look carefully at the animation. You can see that points 1 and 3 are independently moving with constant velocity. There is even a counter where the ratio is 1:2.
This independence is possible if point T1 rests at k step, and point T3 rests at k+1 step, so the equation is as follows:
p1(k)*xT1+p2(k)*xT3, where at p1(k)=0, p1(k)=1 and p1(k+1)=1, p1(k+1)=0
We don't forget the main thing, the constancy of the velocities T1 and T3. Therefore, we divide the whole right-hand side by the sum of the velocities T1 and T2/a. The coefficient a is a constant value, which is needed for T3 to reach the given value at β=90°
I got that the absolute velocity of point 3 exceeds the absolute velocity of point 1 by about one third.
I will post the full animation when changing T3 later. In smath I can try to help to repeat it.
[/ENG]


bird.mov (206 КиБ) скачан 26 раз(а).

Wrote

Can we create this in SMath?
Help me please.

There are three things you can watch forever: fire, water, and this and same animations.

Wrote

Wrote

Can we create this in SMath?
Help me please.

There are three things you can watch forever: fire, water, and this and same animations.

See please one my try
Cross-Cyrcle-Bird.sm (51 КиБ) скачан 32 раз(а).

Wrote

[RUS]Будем считать ее не только художественной[/RUS]
[ENG]Let's consider it not only artistic[/ENG]

[RUS]Похоже, что художественная. Во всяком случае отношение скоростей на каждом участке разнится. Намучился я с параметризацией.[/RUS]
[ENG]Looks artistic. In any case, the velocity ratio is different on each section. I've had a lot of trouble with parameterization.[/ENG]
Файл не найден.Файл не найден.
bird1.mov (413 КиБ) скачан 33 раз(а).

Dieses Ziel, was immer es sei, ist mir gar nichts, die Bewegung alles!
В переводе на русский это:
Анимация - ничто, файл - все!
Attach please the sm-file!