Read more in the attached work sheet.

Jean




Solve Systems [Implicit, Linear].sm (50 КиБ) скачан 57 раз(а).

... hee is the "Solve ROBUST Scanner"



Solve ROBUST.sm (12 КиБ) скачан 53 раз(а).

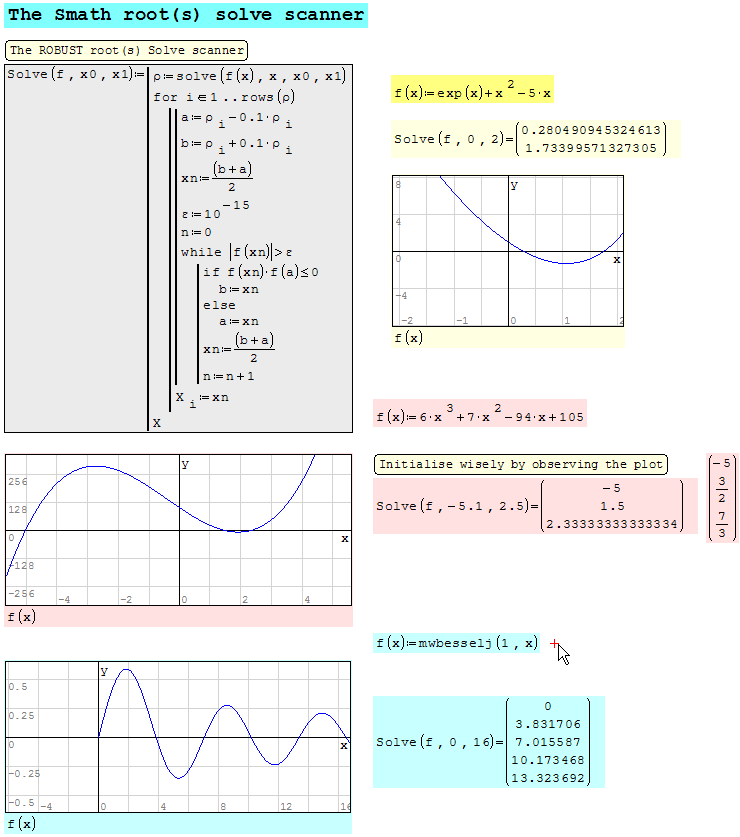
Here is a decent answer: it is known in mathematics that solving for
root(s) and by same token solving for "root(s) intersection" is a
difficult task. For instance, in Mathcad we may get no answer if TOL
is not compatible. It may be as low as default 0.001 and get exact
root. But it may require much lower TOL. Maxima "solve" is no different
maths wise. They have simplified the block by not including user TOL,
and probably concluded that TOL= 10e-9 was generally good enough.
In various applications, "Maxima solve" gets exact root(s) or not better
than 10e-8.
This revised version includes user TOL in the solver. Some examples support
TOL 10e-14 ... other only 10e-12. In any case it should solve.
The two solvers are given: root(s) & "root(s) intersection"


Solve ROBUST.sm (22 КиБ) скачан 64 раз(а).

Nice approach

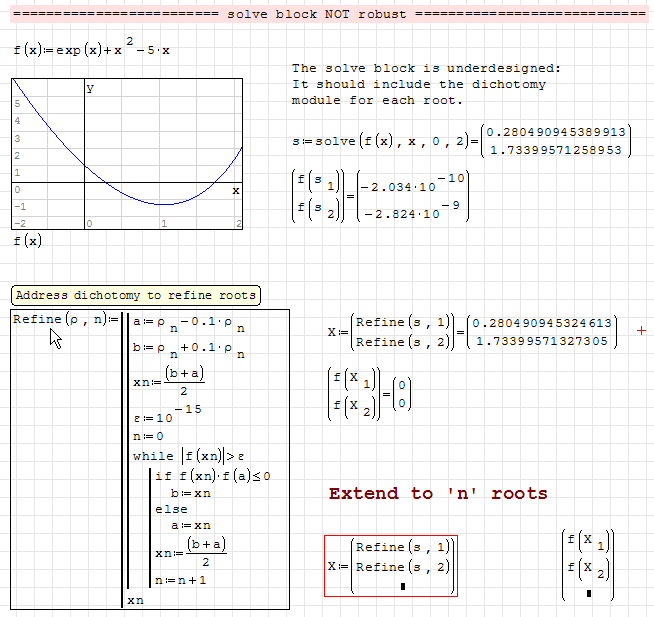
In the other hand, I guess that if solutions are far from 0, the use of +0.1/-0.1 to create the bounds might be a problem (f.e. if the solution was 10000, the domain would be [9000,11000]; this means nothing without a function, but in general might cause issues). Maybe some "adaptive algorithm" may be added to improve this point.

Wrote

Nice approach

In the other hand, I guess that if solutions are far from 0, the use of 0.1/-0.1 to create the bounds might be a problem (f.e. if the solution was 10000, the domain would be [9000,11000]; this means nothing without a function, but in general might cause issues). Maybe some "adaptive algorithm" may be added to improve this point.

You are right Davide. Mathcad 'root' is more savantly coded, from recollection two names
come to mind: Brent-Mueller. I have never seen the code. The big-bang technique [±0.1]
made my Sharp calculator work in 1986 as root solve substitute.



This odd case can be rescued by user, either manually or via "stripping".
The "ROBUST" proposal should help in most Smath applications.

Cheers, Jean