Список функций:
rkfixed(), Rkadapt(),
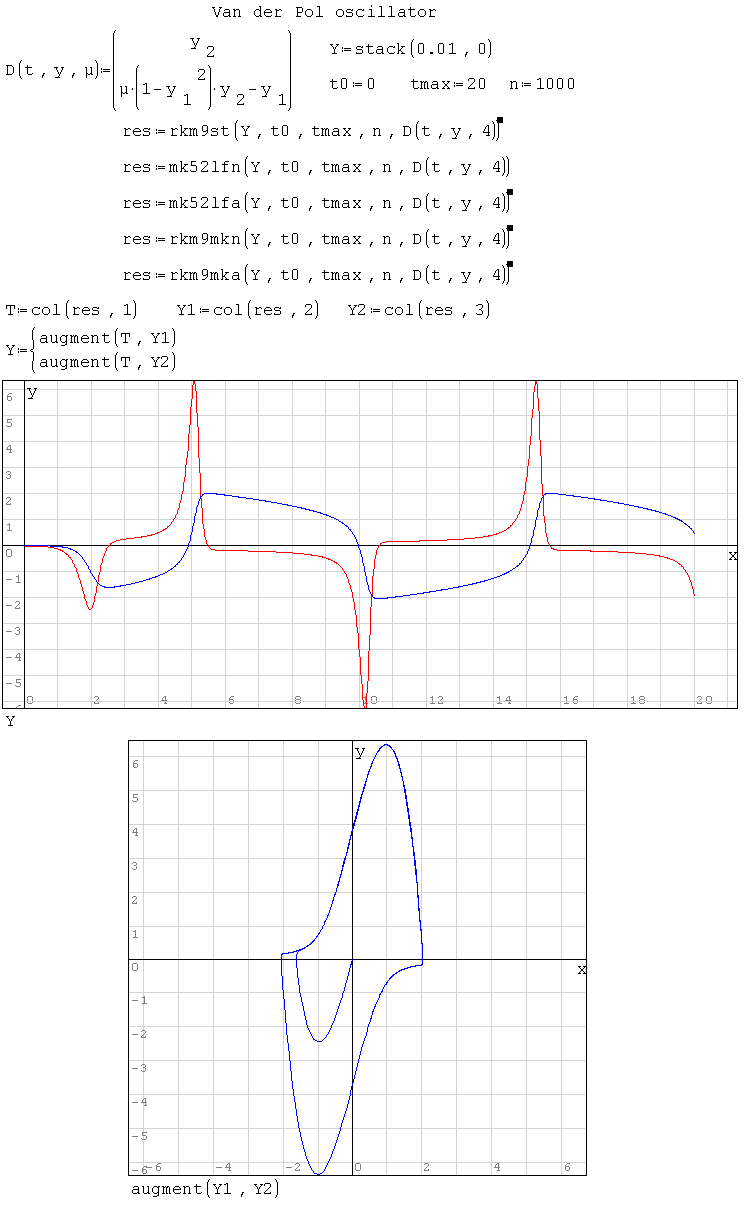
rkm9st(), mk52lfn(), mk52lfa(), rkm9mkn(), rkm9mka().

---

Решатели нежёстких систем ОДУ:

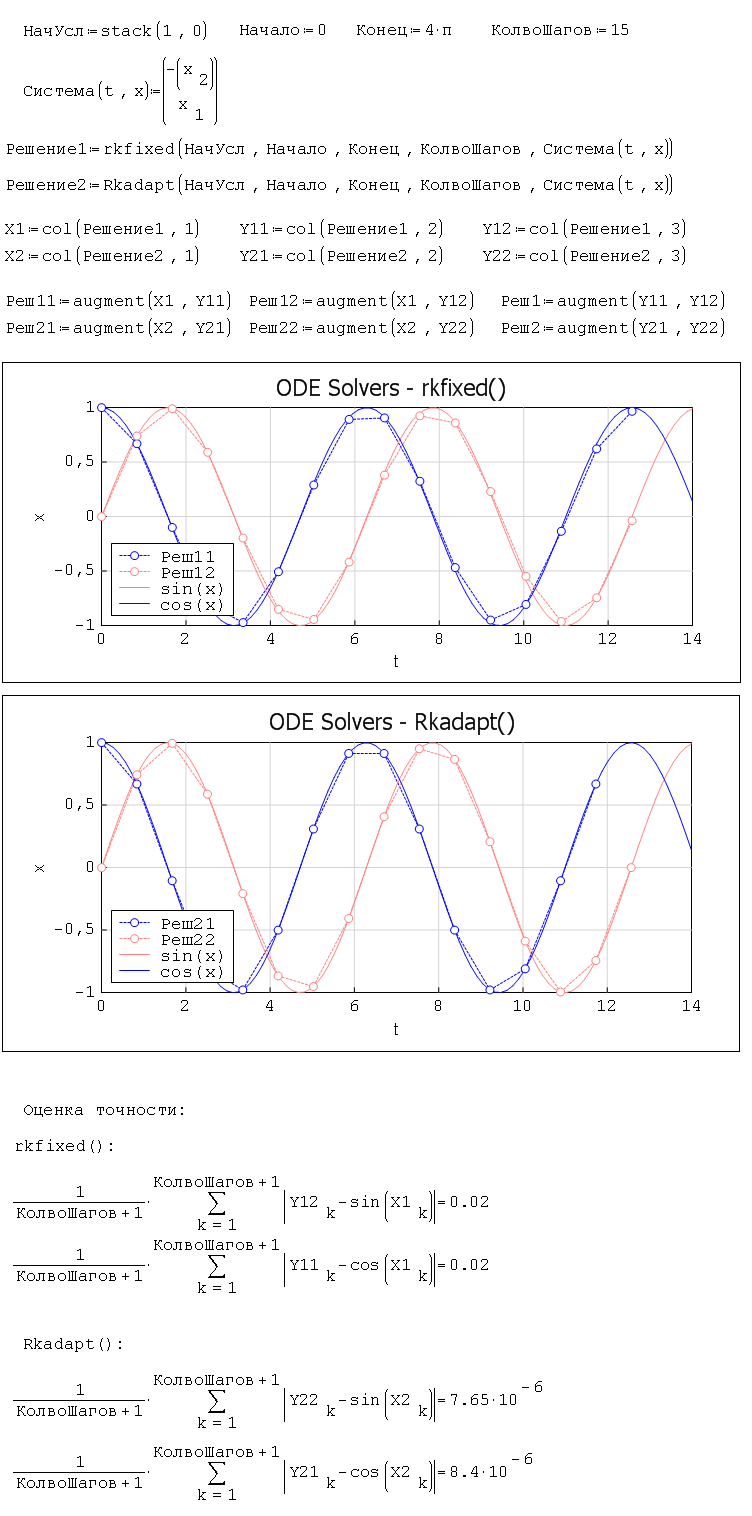
rkfixed(init, x1, x2, intvls, D) Uses the fourth-order Runge-Kutta fixed-step method.

Rkadapt(init, x1, x2, intvls, D) Uses the fourth-order Runge-Kutta with adaptive step-size.

Intel ODE Solvers Library:

rkm9st(init, x1, x2, intvls, D) A specialized routine for solving non-stiff and middle-stiff ODE systems using the explicit method, which is based on the 4th order Merson’s method and the 1st order multistage method of up to and including 9 stages with stability control.

mk52lfn(init, x1, x2, intvls, D) A specialized routine for solving stiff ODE systems using the implicit method based on L-stable (5,2)-method with the numerical Jacobi matrix, which is computed by the routine.

mk52lfa(init, x1, x2, intvls, D) A specialized routine for solving stiff ODE systems using the implicit method based on L-stable (5,2)-method with numerical or analytical computation of the Jacobi matrix. The user must provide a routine for this computation.

rkm9mkn(init, x1, x2, intvls, D) A specialized routine for solving ODE systems with a variable or a priori unknown stiffness; automatically chooses the explicit or implicit scheme in every step and computes the numerical Jacobi matrix when necessary.

rkm9mka(init, x1, x2, intvls, D) A specialized routine for solving ODE systems with a variable or a priori unknown stiffness; automatically chooses the explicit or implicit scheme in every step. The user must provide a routine for numerical or analytical computation of the Jacobi matrix.


Параметры:

- init is either a vector of n real initial values, where n is the number of unknowns (or a single scalar initial value, in the case of a single ODE - not implemented yet).
- x1 and x2 are real, scalar endpoints of the interval over which the solution to the ODE(s) is evaluated. Initial values in init are the values of the ODE function(s) evaluated at x1.
- intvls is the integer number of discretization intervals used to interpolate the solution function. The number of solution points is the number of intervals + 1.
- D is a vector function of the form D(x,y) specifying the right-hand side of the system

Показать спойлер

[albumimg]119[/albumimg] [albumimg]141[/albumimg] [albumimg]272[/albumimg]

Ссылки:

1. Intel ODE Solvers Library.

---

ODE_manual.pdf (239 КиБ) скачан 311 раз(а).

Текст функции rkfixed
http://communities.ptc.com/videos/1471
Текст функции rkadapt
http://twtmas.mpei.ac.ru/mas/worksheets/rkadapt.mcd
если это кому интересно.

Спасибо, Валерий Фёдорович, приму во внимание.

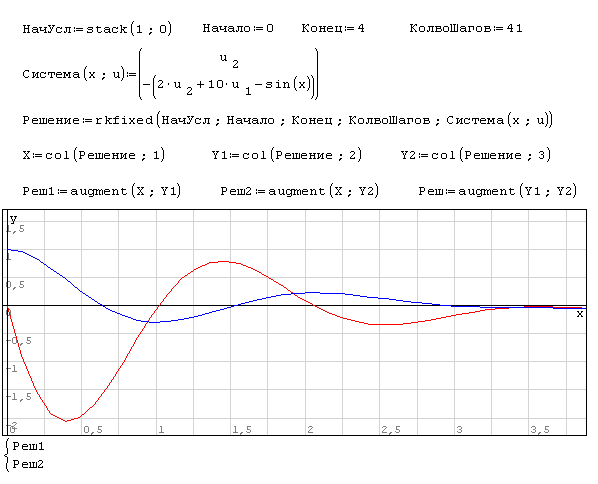
Вот плагин с функцией rkfixed(): ODESolvers.dll
Исходник: ODESolvers_Class1.pdf
Вот примерный документ: rkfixed.sm

Примечания:
1. Функция системы должна быть вектором.
2. Имена переменных (t,x) могут быть любыми.

П.С. Там в цикле while() есть небольшая ошибка.
Поскольку это всё равно транслятор, то работает относительно медленно.
Самое смешное, что аналогичная функция, написанная в документе в виде программного блока работает всего на немного медленнее этой реализации ("подушка" посчиталась на 30 секунда быстрее, всего время расчёта для rkfixed() на моём компе около 3 мин 10 сек).
Здесь (n+2) теоретически может превысить размер вектора элементов системы. Надо будет поправить на досуге.

Спасибо за плагин.

Wrote

Исходник: ODESolvers_Class1.pdf

Личным сообщением на форуме послал Вам логин и пароль для доступа к репозиторию на запись. Думаю удобнее код будет иметь там.

Да, я заметил логин и пароль, спасибо. Пока не буду мусорить в репозитории. Последний год я привык писать на русском (пишу в одиночку), а в репозиторий нужно переписывать всё на английском. Пока лень.

Если добавить ещё несколько решателей, то, пожалуй, можно будет их залить. Меня не устраивает скорость работы. Всё равно медленно.

В качестве тестовой версии предлагаю Rkadapt(). Исходник является компиляцией кода Валерия Фёдоровича и приведённого в книжке "Numerical Recipes in C", откуда он собственно и был взят. Я подгонял его под фиксированные шаги как в Маткаде, чтобы вызов их был идентичен. Получилось не совсем ещё хорошо, но пока работает.

Примечание. Возможны случаи при большом количестве шагов (больше 100, к примеру), когда в конце вектора решения будут один или несколько нулей.

Плагин: ODESolvers.dll
Документ: Rkadapt.sm

Лучше тестируйте вот эту версию: ODESolvers.dll От 12.11.2010 г.

Здесь я уже понял ту фишку, которую использовали маткадовцы, когда адаптивный шаг "пристраивали" к фиксированной сетке. Работает гораздо быстрее и правильнее. Убрал многие ошибки. Теперь получается тоже, что и с rkfixed(), но гораздо точнее в тех же точках.

Андрей, тут я заметил одну проблему, когда правил плагин:

Функция if разбирается только в Preprocessing и не определяется в численной и/или символьной библиотеках.

Да, это даже наверное логично. Исправил плагин: ODESolvers.dll


Алгоритм Rkadapt(): Rkadapt prog.sm
К сожалению, я не смог заставить его работать, т.к. не понял где ошибка в записи выражения.
Здесь ещё нет защиты от зацикливания при выборе шага.

Ещё пример работы:

Эксперименты с ушами:

Обновлён. Добавлены функции из Intel ODE Solvers Library: rkm9st(), mk52lfn(), mk52lfa(), rkm9mkn(), rkm9mka().

Также как и в DotNumerics можно использовать переменные AbsTol и RelTol в документе для задания точности вычислений.

---

ODE_manual.pdf (239 КиБ) скачан 110 раз(а).