1 страниц (7 вхождений)
Пошаговое решение СЛАУ и нахождение обратных матриц - Сообщения
#1 Опубликовано: 07.12.2009 22:05:13
Подскажите, пожалуйста, как решать СЛАУ методом Гаусса в Smath
#2 Опубликовано: 07.12.2009 22:32:02
Если Вы хотите получить ответ, то нет разницы каким методом решать задачу - пользуйтесь формулой [MATH]A^{-1}*B[/MATH]. Если же Вам необходимо получить решение шаг за шагом, то, к сожалению, SMath Studio не способна его показать.
#3 Опубликовано: 07.12.2009 22:37:06
Нет, нам задали не просто получить ответ, а именно методом Гаусса решить систему. То есть вообще нельзя никак это показать, кроме как набором вручную?
#4 Опубликовано: 07.12.2009 23:09:26
Хорошо, а можно составить программу, которая приводит матрицу к треугольному виду?
#5 Опубликовано: 08.12.2009 00:10:59
Создал для Вас файл/программу: https://smath.com/files/Download/RaP3p.
На выходе получается следующее:
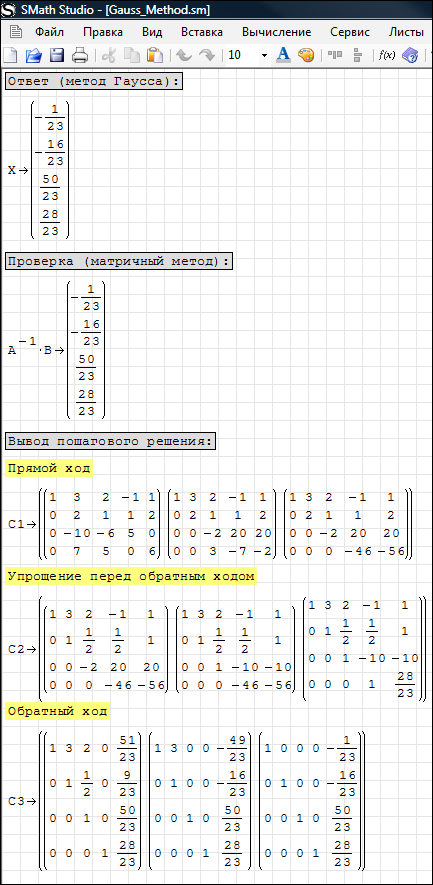
Как видно из скриншота программа показывает результаты последовательных действий. В прямом ходе (C1) происходит преобразование матрицы к верхней треугольной. Вторым шагом (C2) программа элементарными преобразованиями добивается, что бы на главной диагонали были единицы. В обратном ходе (C3) SMath Studio приходит к единичной матрицы слева.
Единственное о чём Вам требуется подумать, так это об оформлении, т.к. в ВУЗах требуется указание производимых действий. Можно, конечно, доработать файл, что бы тот и текущие действия показывал, но рассчёт станет менее читабельным да и не так-то это сложно - понять, что сделала программа от действия к действию.
Данный файл расчётов может не только пошагово показать ход поиска решений системы линейных алгебраических уравнений (СЛАУ), но и найти обратную матрицу, опять же, с полным выводом решения.
Надеюсь это то, что Вам нужно. С уважением, Андрей Ивашов.
На выходе получается следующее:
Как видно из скриншота программа показывает результаты последовательных действий. В прямом ходе (C1) происходит преобразование матрицы к верхней треугольной. Вторым шагом (C2) программа элементарными преобразованиями добивается, что бы на главной диагонали были единицы. В обратном ходе (C3) SMath Studio приходит к единичной матрицы слева.
Единственное о чём Вам требуется подумать, так это об оформлении, т.к. в ВУЗах требуется указание производимых действий. Можно, конечно, доработать файл, что бы тот и текущие действия показывал, но рассчёт станет менее читабельным да и не так-то это сложно - понять, что сделала программа от действия к действию.
Данный файл расчётов может не только пошагово показать ход поиска решений системы линейных алгебраических уравнений (СЛАУ), но и найти обратную матрицу, опять же, с полным выводом решения.
Надеюсь это то, что Вам нужно. С уважением, Андрей Ивашов.
#6 Опубликовано: 09.12.2009 16:01:15
Большое спасибо!!!!!!!!!

1 страниц (7 вхождений)
- Новые сообщения
- Нет новых сообщений
