1 страниц (10 вхождений)
Simple solve - Solving simple equation returns "no real roots" - Сообщения
Hi, is it normal that SMath Studio does not solve simple equation:
while it solves 1/X-1=4 ?
Michał
solve(1/(X-1)=8,X)Michał
In fact it should not be necessary to define the search range of solutions. A search range is still defined in the general options, and sometimes you need to take a look before you run.
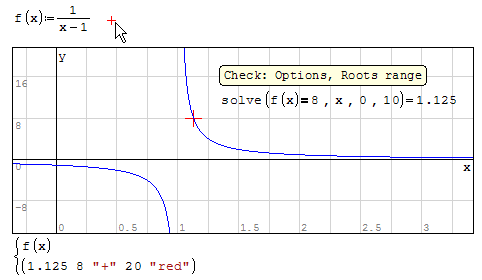
The discontinuity of the function at x = 1 creates some numerical problem.
As shown in the figure, trying different intervals are obtained unexpected values.
[albumimg]1436[/albumimg]
sergio
The discontinuity of the function at x = 1 creates some numerical problem.
As shown in the figure, trying different intervals are obtained unexpected values.
[albumimg]1436[/albumimg]
sergio
... always plot before solving, bracket the range wisely [1,2]
1 пользователям понравился этот пост
Davide Carpi 06.05.2016 15:09:00
They both solve nicely. Search for the bracketing that
is compatible with the function(s)3.12345789 is typical.
It does not need to be so weird.
Jean
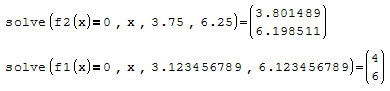
Forum eq.sm (28,6 КиБ) скачан 800 раз(а).
is compatible with the function(s)3.12345789 is typical.
It does not need to be so weird.
Jean
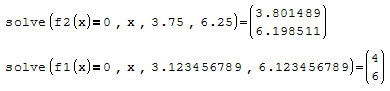
Forum eq.sm (28,6 КиБ) скачан 800 раз(а).
On a previous post, I was "schooled" about using the solve(4) instead of the solve(2) as a default. IMHO, the Solve(2) only function part of the time. I no longer consider it and think it should be removed as a builtin function ... at least, that is how I now treat Solve(2). This goes hand in hand with Jean's "solution"
BTW, Jean, I never got you PM. I sent you a second one with my email address.
BTW, Jean, I never got you PM. I sent you a second one with my email address.
Elsid,
My mail box "Sent items"
Thanks Elsid,
Mathcad 11.2a crashed Mona Zeftel at PTC .
Vice versa: collabs converting 14/15 back to 11
would open in my 11, but unusable .
Shortly after the silence from PTC, the warflame ended.
So, my web site may be useful to some old Mathcad 11 Enterprise.
Have a good day, take care.
Jean
My mail box "Sent items"
Thanks Elsid,
Mathcad 11.2a crashed Mona Zeftel at PTC .
Vice versa: collabs converting 14/15 back to 11
would open in my 11, but unusable .
Shortly after the silence from PTC, the warflame ended.
So, my web site may be useful to some old Mathcad 11 Enterprise.
Have a good day, take care.
Jean
Quite right Elsid: Solve(2) does not work because it is not installed
in the Smath 5346. "solvers" are all home made on some representative
functions, thus are prone to fails ... particularly with Smath that
is only 32 bits , no extended floating point [Smath 5346].
The "Dichotomy" is much less prone to fail. I never understood why some
Maxima stuff works in 5346 and most fails. "Re-initialise under settings"
Re-initialise What ? Isn't the task of the plugins manager ?
Jean, clean version attached.
Solve Dichotomy.sm (19,97 КиБ) скачан 811 раз(а).
in the Smath 5346. "solvers" are all home made on some representative
functions, thus are prone to fails ... particularly with Smath that
is only 32 bits , no extended floating point [Smath 5346].
The "Dichotomy" is much less prone to fail. I never understood why some
Maxima stuff works in 5346 and most fails. "Re-initialise under settings"
Re-initialise What ? Isn't the task of the plugins manager ?
Jean, clean version attached.
Solve Dichotomy.sm (19,97 КиБ) скачан 811 раз(а).
... so, let's revisit f1(x). This function will reach infinity @ x=5. You can see that by inspection.
log(x-5,0.5)=ln(-5+x)/ln(1/2). What that means is that in the "bisection" process, if the bracketed
values do create '5', it won't go any further. It won't go any further as long as as the mean of the
bracketed values will be symmetric @ '5' ... (3.75+6.25)/2 = 5.
In that case and in any real application or Edu.Quiz, it is necessary and sufficient to create
asymmetry to escape the bisection = 5. You may argue that (3.95+6.05)/2 is exactly '5'. Yes it is
but it is paper pencil but not numerically wrt to the [/] divide operator, and that invisible asymmetry
is now sufficient to escape the bisection from being excatly '5'.
solve(f1(x)≡0,x,3.95,6.05)=mat(4,6,2,1)... the two solutions are found.
That additional comment is in advance to more questions and similar application case(s).
Jean
log(x-5,0.5)=ln(-5+x)/ln(1/2). What that means is that in the "bisection" process, if the bracketed
values do create '5', it won't go any further. It won't go any further as long as as the mean of the
bracketed values will be symmetric @ '5' ... (3.75+6.25)/2 = 5.
In that case and in any real application or Edu.Quiz, it is necessary and sufficient to create
asymmetry to escape the bisection = 5. You may argue that (3.95+6.05)/2 is exactly '5'. Yes it is
but it is paper pencil but not numerically wrt to the [/] divide operator, and that invisible asymmetry
is now sufficient to escape the bisection from being excatly '5'.
solve(f1(x)≡0,x,3.95,6.05)=mat(4,6,2,1)... the two solutions are found.
That additional comment is in advance to more questions and similar application case(s).
Jean
1 страниц (10 вхождений)
- Новые сообщения
- Нет новых сообщений