I've been diving into partial derivatives, but I think I am making a basic tool-use error as the calculated derivative contributions are all zero:

20220424 Simple Voltage Divider with Tolerances A3.sm (56 КиБ) скачан 28 раз(а).

Thank you in advance.

Hi. The quick solution: Put the definition of V.out before the values definitions (and change DRA by DR1).

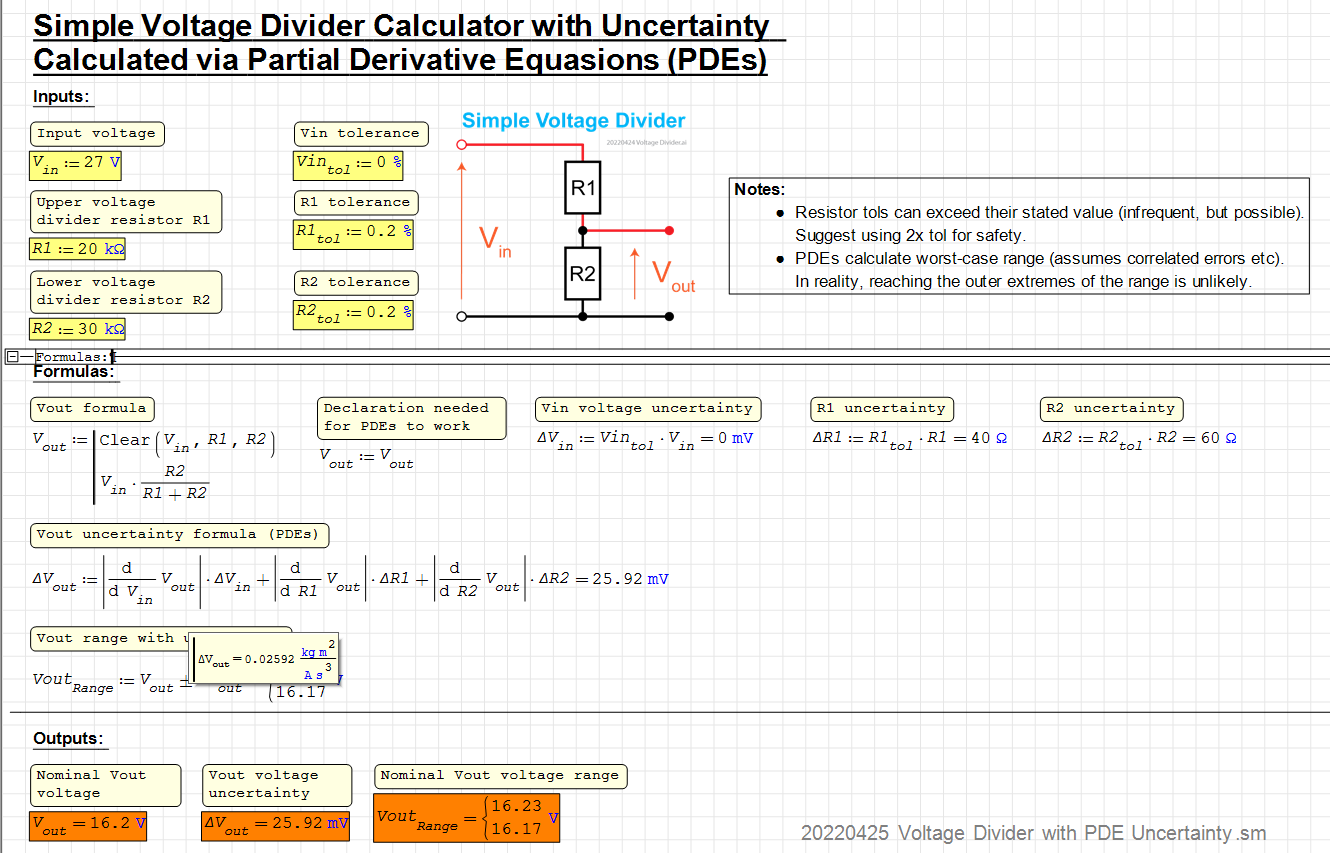
The technical solution: Use V.out(V.in,R1,R2) instead V.out. The only problem is that this way the expression for calculating the error is very long, visually.

The intermediate solution: unassign the variable "inside" the definition of V.out.



The main reason: like in mathcad, in smath the numerical derivation does not follow the usual rules of evaluation and does what is "Hold" in wolfram mathematica and "uneval" in maple.

Best regards.
Alvaro.

Hi. The attached have two functions for automating the process of work with absolute or relative uncertainties from the formula of a magnitude.

Abs and Rel Uncertainty.sm (63 КиБ) скачан 39 раз(а).
Abs and Rel Uncertainty.pdf (169 КиБ) скачан 50 раз(а).

Best regards
Alvaro

Thank you Alvaro, that is fantastic.

I shall dig in and learn about the automated summations.

A good reminder too: it is uncertainty being calculated (not variance). Fixed above.

If you have patience, read BIPM on all that.
Example 2 is the ± error reading for an installed T/C [Thermocouple]
Each individual is in Engineering ± from supplier.
Not so much in this example ... but lot more at higher operating temperature.
You can reach way above ± 1 °C, so important for Control Room Operators.
Cheers ... Jean.

Uncertainty.sm (8 КиБ) скачан 26 раз(а).

Wrote

If you have patience, read BIPM on all that.
Example 2 is the ± error reading for an installed T/C [Thermocouple]
Each individual is in Engineering ± from supplier.
Not so much in this example ... but lot more at higher operating temperature.
You can reach way above ± 1 °C, so important for Control Room Operators.
Cheers ... Jean.

Uncertainty.sm (8 КиБ) скачан 26 раз(а).

Thanks Jean. RMS error combining is not the same thing though (that is making assumptions about likelihood of variance/SDs).

A good explanation from Texas Instruments is attached.
snva112a.pdf (291 КиБ) скачан 31 раз(а).

Wrote

Thanks Jean. RMS error combining is not the same thing though (that is making assumptions about likelihood of variance/SDs).

You are right Mark from the stand point of designing/specifying a new product.
From the Project Engineer, you go with what you you have in hand and from Standards.
That Magnesium Plant 35 year ago, worth today > 5 billions US $
was critical about temperature. I spent days for T/C.
One supplier offered special lab selection at reasonable cost.
On the turnkey day ... firework/music, Champagne.
That big Hawai telescope, toke two years to cool down ambient.
Take care Mark ... Jean.

My personal path to understand RMS values, from the origin of the measurements for the classical theories (Newton & Maxwell eqs, not general relativity or quantum mechanics observables)

- Numerals or ordinal numbers: indicate the position, not the quantity (a soccer player with a number 3 plays in defense on the left, and with 7 he attacks on the right). Defined by Peano axioms, the definition of slices of continuous class pairs that are sequences of rationals leads to reals.

- Cardinal numbers: the number of elements in a set, defined with Cantor axioms and with the completeness they lead to the real ones.

- Probability. The correspondence (homeomorphism) between the logical functions and, or and not, the theory of sets with the operations union, intersection and complement and the theory of probability was established by Kolmogorov defining a sigma algebra between the probability distributions of random variables. With the central limit theorem, they constitute a full-fledged measure theory. The definitions that matter are the expectation E(x) and the variance.

This is what is used in the BIPS guide, which is the "official" standard for uncertainties and errors:

https://www.bipm.org/documents/20126/2071204/JCGM_100_2008_E.pdf/cb0ef43f-baa5-11cf-3f85-4dcd86f77bd6

What they don't explain in the guide is how or why they introduce partial derivatives (actually the gradient) or justify the use of least squares. The theory behind this is the linear algebra of vector spaces with infinite base elements. In this environment, the adjustment of least squares is equivalent to the expansion in series (such as Fourier) measuring the distances and the norm of a function through a scalar product that is introduced as a convolution integral, and given Since the function has "components" (the coefficients of the series in an orthogonal basis) I can define "distances" between two functions, since I calculate them as the distances between the two vectors, and to minimize it, with Parseval's identity and the Cauchy-Schwartz inequality.

The little formula of the absolute values ​​of the partial derivatives seems silly, but it can also be justified in this way, since it is the scalar product of the gradient norm (although not Euclidean, but simply defined by the absolute values ​​of the components) times the vector of uncertainties, for which it measures a distance: the one that is supposed to exist between the "true value" (which exist in classical, not relativistic or quantum physics) and the one being measured.

Does all this serve a purpose? Maybe yes. Here is how to get the RMS value in matlab of a signal (it can be easily translated to SMath. The signal can be a voltage, an amperage, a frequency or any other periodic magnitude)

https://www.gaussianwaves.com/2015/07/significance-of-rms-root-mean-square-value/

Compare the above with the explanation of why you should buy FLUKE "true RMS values" instruments:

https://www.fluke.com/en-us/learn/blog/electrical/what-is-true-rms

Best regards.
Alvaro.

Wrote

What they don't explain in the guide is how or why they introduce partial derivatives (actually the gradient) or justify the use of least squares. The theory behind this is the linear algebra of vector spaces with infinite base elements. In this environment, the adjustment of least squares is equivalent to the expansion in series (such as Fourier) measuring the distances and the norm of a function through a scalar product that is introduced as a convolution integral, and given Since the function has "components" (the coefficients of the series in an orthogonal basis) I can define "distances" between two functions, since I calculate them as the distances between the two vectors, and to minimize it, with Parseval's identity and the Cauchy-Schwartz inequality.

Thank you Alvaro. All about using the right tools for the job, and learning that as we learn more, we need to learn more... without getting paralyzed (the 'good enough' theorem).

I'm using the PDEs as they provide a 'safely over-stated outer bounds' for worst-case circuit design (ie all errors correlated, all absolute vector magnitudes added linearly (ie not Euclidean) which they don't in real-world applications). For my current application, this 'overstatement' of error uncertainty is fine. With more constrained designs I'd have to look at the error distributions, correlations, and confidence intervals (thank you for the uncertainty 'bible'!), and even adjust-on-test, calibration etc (eek).

Wrote

... All about using the right tools for the job, and learning that as we learn more, we need to learn more... without getting paralyzed (the 'good enough' theorem).
...

Yep. I know that filling. To show that the above is quite concrete, in this file the RMS of some typical waveforms are calculated by 3 methods: with integrals, in the time domain and in the frequency domain. I think it is quite immediate to apply these last two methods to a magnitude that you have sampled with a logger.

RMS.sm (36 КиБ) скачан 26 раз(а).
RMS.pdf (246 КиБ) скачан 30 раз(а).

Finally, if the magnitude is periodic, you can get its peak value with the MPeak function here: https://en.smath.com/forum/yaf_postsm69034_Modified-Nodal-Analysis.aspx#post69034 . With that peak value you can easily get also the frequency and the period

Best regards.
Alvaro.

Thanks Alvaro,

I use the latter two all the time.

Integrals require knowledge of the signal, and an integral filter is usually already being applied in most good instruments to notch 50/60Hz mains (and harmonics).

Thank you for your help everybody. Here it is working:

20220425 Voltage Divider with PDE Uncertainty.sm (59 КиБ) скачан 40 раз(а).