1 страниц (11 вхождений)
Analytical solution expected - Equation - Сообщения
Hello Everybody,
Do you see an analytical solution for the equation in x:
Sinh(x) – T*x = 0
As an approximation, I developed sinh(x) in a Taylor series to make a 4th degree equation.
Best regards,
Ioan
Do you see an analytical solution for the equation in x:
Sinh(x) – T*x = 0
As an approximation, I developed sinh(x) in a Taylor series to make a 4th degree equation.
Best regards,
Ioan
Do to others as you would like them to do to you! Knowledge is of no value unless you put it into practice - Chekhov
Hi ioan. If we understand 'analytical expression' as 'closed form', the answer is that there is none. But if the objective is to find the real solution, with as many digits as the precision of the calculator used, then it is enough to remember that real numbers are introduced to be able to calculate limits, so this would be a valid answer.
nr-example.sm (9,37 КиБ) скачан 812 раз(а).
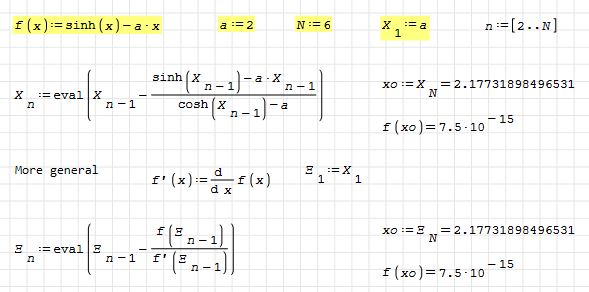
Best regards.
Alvaro.
nr-example.sm (9,37 КиБ) скачан 812 раз(а).
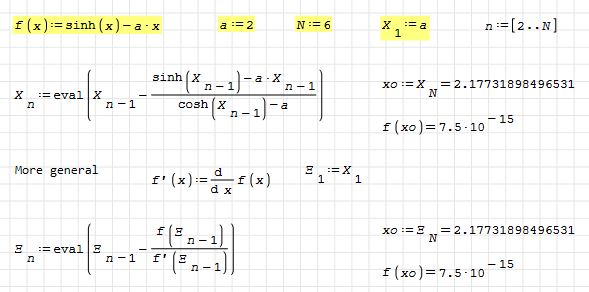
Best regards.
Alvaro.
1 пользователям понравился этот пост
ioan92 30.09.2023 09:50:00
Hi Alvaro,
Thank you very much for your answer.
1. In fact, I’ve already used the Newton solution. I like your elegant iteration control. I used a trivial "for" or "while" command. However, the result’s precision is essentially dependent on the machine’s precision (bytes number on a variable).
2. My problem is an engineering one: the analysis of the catenary structural cables. High numerical precision is not an objective for me.
3. I looked for an explicit mathematical solution, in order to avoid iterations. Really, it’s more a caprice than a necessity. Basically, I hoped to have a simple formula for the intersection of a hyperbolic sinus with an inclined line, but I see that mathematics ways are as well simple as complicated…
4. In the SMath environment there also is a compact, numerical solution based on the "solve" command (see the annexed file).
Thanks again for your kind attention.
Best Regards,
Ioan

nr-example Alvaro & Ioan.sm (20,45 КиБ) скачан 781 раз(а).
Do to others as you would like them to do to you! Knowledge is of no value unless you put it into practice - Chekhov
Hi ioan.
Here the root is expressed as the limit of a recurrent sequence as well, but in terms of basic operations.
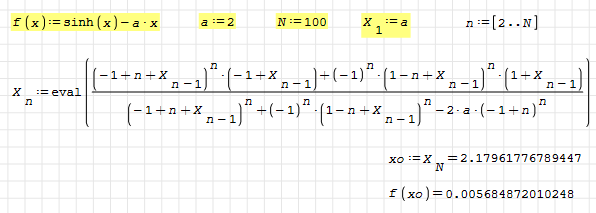
nr-example 2.sm (14,52 КиБ) скачан 808 раз(а).
Best regards.
Alvaro.
Wrote
2. My problem is an engineering one: the analysis of the catenary structural cables. High numerical precision is not an objective for me. [/i]
Here the root is expressed as the limit of a recurrent sequence as well, but in terms of basic operations.
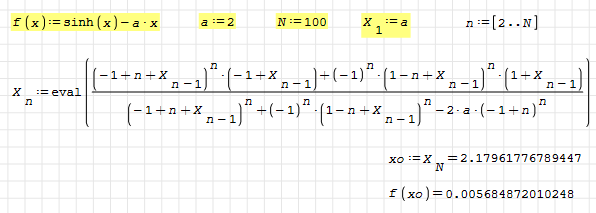
nr-example 2.sm (14,52 КиБ) скачан 808 раз(а).
Best regards.
Alvaro.
1 пользователям понравился этот пост
ioan92 30.09.2023 15:13:00
Hi Alvaro,
Thank you very much for your additional solution.
This last solution seems resulting with a more modest convergence.
The graphical image of the case is:
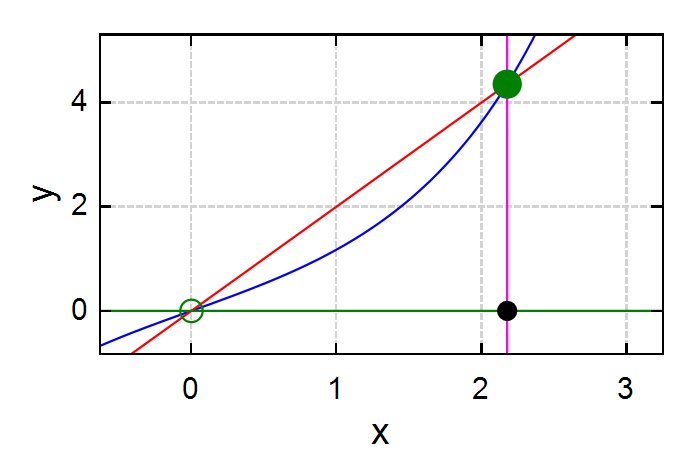
It seems that the 4th degree polynom decomposition of the equation, solved without any iteration is enough reasonable; of course, less compact than the solution based on the solve function
Best regards,
Ioan
Thank you very much for your additional solution.
This last solution seems resulting with a more modest convergence.
The graphical image of the case is:

It seems that the 4th degree polynom decomposition of the equation, solved without any iteration is enough reasonable; of course, less compact than the solution based on the solve function
Best regards,
Ioan
Do to others as you would like them to do to you! Knowledge is of no value unless you put it into practice - Chekhov
Wrote... This last solution seems resulting with a more modest convergence ...
Yes, it is. But it uses only algebraic operations! This other provide a better approximation using actually only one expression, even it is very long (19060 for the string length)
nr-example 3.sm (9,03 КиБ) скачан 796 раз(а).

Best regards.
Alvaro.
1 пользователям понравился этот пост
ioan92 01.10.2023 16:03:00
Hi Alvaro,
I’m pleased to read you again.
I turn around with this equation from some time and, as usual, I touched my limits, so it is stimulating to see also some different regards.
I enjoyed very much your elegant and compact solution based on the Newton method.
Comparing your Newton type solution with one of mine, I noted some differences, namely:
I also used a dichotomy solution. It is very efficient and almost the best solution.
Finally, I mention that I developed a solution without iterative, based on the development of the hyperbolic sinus. The obtained equation is of 4th degree, solved with the classical direct symbolic solution.
I also used the “solve” command with a very compact form but with enough long work time for iterations.
I made a "time contest" with this various solutions.
Let me know if you appreciate as useful some details.
Thanks again for your kind attention.
Best Regards,
Ioan
I’m pleased to read you again.
I turn around with this equation from some time and, as usual, I touched my limits, so it is stimulating to see also some different regards.
I enjoyed very much your elegant and compact solution based on the Newton method.
Comparing your Newton type solution with one of mine, I noted some differences, namely:
• In order to reach the acceptable solution with the smallest number of iterations, there are two significant parameters: i) the starting point of the variable and ii) the control (stop) of iterations once the wished precision is reached.
• I mention that for my purposes, the range of the value a = [1.0001..10].
• For the starting value of the variable, you used simply the “a” value. For the starting point, I obtained a simple value based on the development of the second order of the hyperbolic sinus. Such a starting value diminish significatively the iteration number. You give arbitrarily a number of iterations; I control the convergence inside a “while” cycle.
• I mention that for my purposes, the range of the value a = [1.0001..10].
• For the starting value of the variable, you used simply the “a” value. For the starting point, I obtained a simple value based on the development of the second order of the hyperbolic sinus. Such a starting value diminish significatively the iteration number. You give arbitrarily a number of iterations; I control the convergence inside a “while” cycle.
I also used a dichotomy solution. It is very efficient and almost the best solution.
Finally, I mention that I developed a solution without iterative, based on the development of the hyperbolic sinus. The obtained equation is of 4th degree, solved with the classical direct symbolic solution.
I also used the “solve” command with a very compact form but with enough long work time for iterations.
I made a "time contest" with this various solutions.
Let me know if you appreciate as useful some details.
Thanks again for your kind attention.
Best Regards,
Ioan
Do to others as you would like them to do to you! Knowledge is of no value unless you put it into practice - Chekhov
Your long ... resumes to root Dichotomy for real Engineering projects.
Engineering functions that are in spline style are not analytical.
My Smath is immensely rich of fitting methods ... conclusively analytical.
Engineering functions that are in spline style are not analytical.
My Smath is immensely rich of fitting methods ... conclusively analytical.
Hi ioan. Dichotomy is always better because it provides an interval of the solution. Here, some other notes:
You're right: the start value is part of the solution, and it requires better attention. This version uses different guess values.

This other is an Improved Ostrowskiroot-finding method, by Miquel Grau & Jose Luis Diaz-Barrero
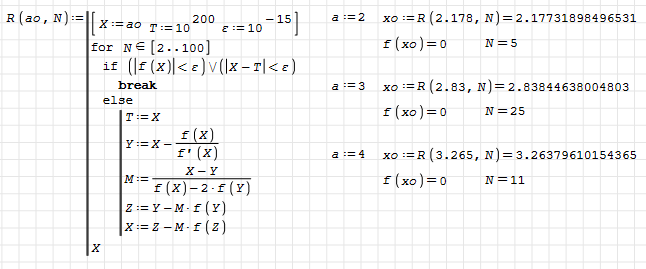
nr-example 3.sm (19,28 КиБ) скачан 773 раз(а).
Best regards.
Alvaro.
You're right: the start value is part of the solution, and it requires better attention. This version uses different guess values.

This other is an Improved Ostrowskiroot-finding method, by Miquel Grau & Jose Luis Diaz-Barrero
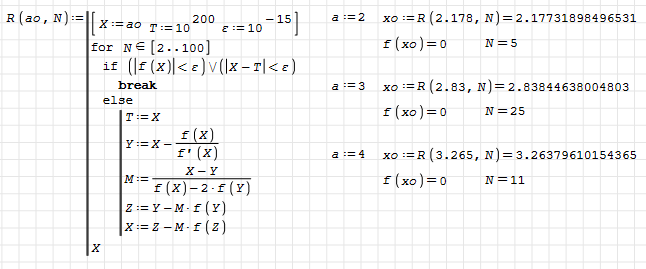
nr-example 3.sm (19,28 КиБ) скачан 773 раз(а).
Best regards.
Alvaro.
1 пользователям понравился этот пост
ioan92 02.10.2023 05:07:00
Hi Alvaro,
Thank you for your last improvements.
I see that my mathematics end only as a modest engineering tool, while yours seams going much further.
In the appended file, I synthesized my available answers.
Ioan Synthesis 20231002.sm (66,68 КиБ) скачан 811 раз(а).
Please take a look and make any improvements that you feel as appropriate.
I’m sorry, I hadn’t included too much commentary, hoping that things are comprehensible enough as they are in the context of the whole thread.
I noted a large range of results. However, for my purposes,Ioan Synthesis 20231002.sm (66,68 КиБ) скачан 811 раз(а). the available results satisfy my expectations. Now I reached “my incompetence level” (according to Peter’s principle) …
I still have another equation bothering my tranquility, but this maybe for another occasion.
With all my gratitude please receive
My Greetings from Paris,
Ioan
Finally, I mixed my raw first approximation with your last findings and here it is:
![2023-10-02[SelectPlus.sm_].png](/ru-RU/files/Download/B4r2dP/2023-10-02[SelectPlus.sm_].png)
Thank you for your last improvements.
I see that my mathematics end only as a modest engineering tool, while yours seams going much further.
In the appended file, I synthesized my available answers.
Ioan Synthesis 20231002.sm (66,68 КиБ) скачан 811 раз(а).
Please take a look and make any improvements that you feel as appropriate.
I’m sorry, I hadn’t included too much commentary, hoping that things are comprehensible enough as they are in the context of the whole thread.
I noted a large range of results. However, for my purposes,Ioan Synthesis 20231002.sm (66,68 КиБ) скачан 811 раз(а). the available results satisfy my expectations. Now I reached “my incompetence level” (according to Peter’s principle) …
I still have another equation bothering my tranquility, but this maybe for another occasion.
With all my gratitude please receive
My Greetings from Paris,
Ioan
Finally, I mixed my raw first approximation with your last findings and here it is:
![2023-10-02[SelectPlus.sm_].png](/ru-RU/files/Download/B4r2dP/2023-10-02[SelectPlus.sm_].png)
Do to others as you would like them to do to you! Knowledge is of no value unless you put it into practice - Chekhov
1 пользователям понравился этот пост
Alvaro 03.10.2023 09:47:00
Hi Ioan. Looks like a pretty complete and extensive study of an equation that Wolfram Alpha can't solve for the general case, and does not show the intermediate steps for the numerical case.
Best regards.
Alvaro.
Best regards.
Alvaro.
1 пользователям понравился этот пост
ioan92 03.10.2023 04:38:00
1 страниц (11 вхождений)
- Новые сообщения
- Нет новых сообщений
