DotNumerics - SMath

#21 Опубликовано: 01.08.2018 12:54:24

Вячеслав Мезенцев

1 518 сообщений из 1 825 понравились пользователям.

Группа: Moderator

Simple test 2.

DotNumerics.ode.test2.sm (21,23 КиБ) скачан 557 раз(а).
DotNumerics.ode.test2.pdf (79,99 КиБ) скачан 318 раз(а).

Russia ☭ forever, Viacheslav N. Mezentsev

2 пользователям понравился этот пост

sergio 01.08.2018 18:06:00, Radovan Omorjan 02.08.2018 03:05:00

#22 Опубликовано: 01.08.2018 21:57:14

Jean Giraud

983 сообщений из 6 866 понравились пользователям.

Группа: User

Wrote
Simple test 2.

Works nice conventional/visual [6179].
That document, if it would come from other designer
would pass my QA [Quality Assurance].

Jean

DotNumerics.ode.test2.sm (24,51 КиБ) скачан 557 раз(а).

#23 Опубликовано: 09.09.2018 14:23:36

Martin Kraska

1 280 сообщений из 2 202 понравились пользователям.

Группа: Moderator

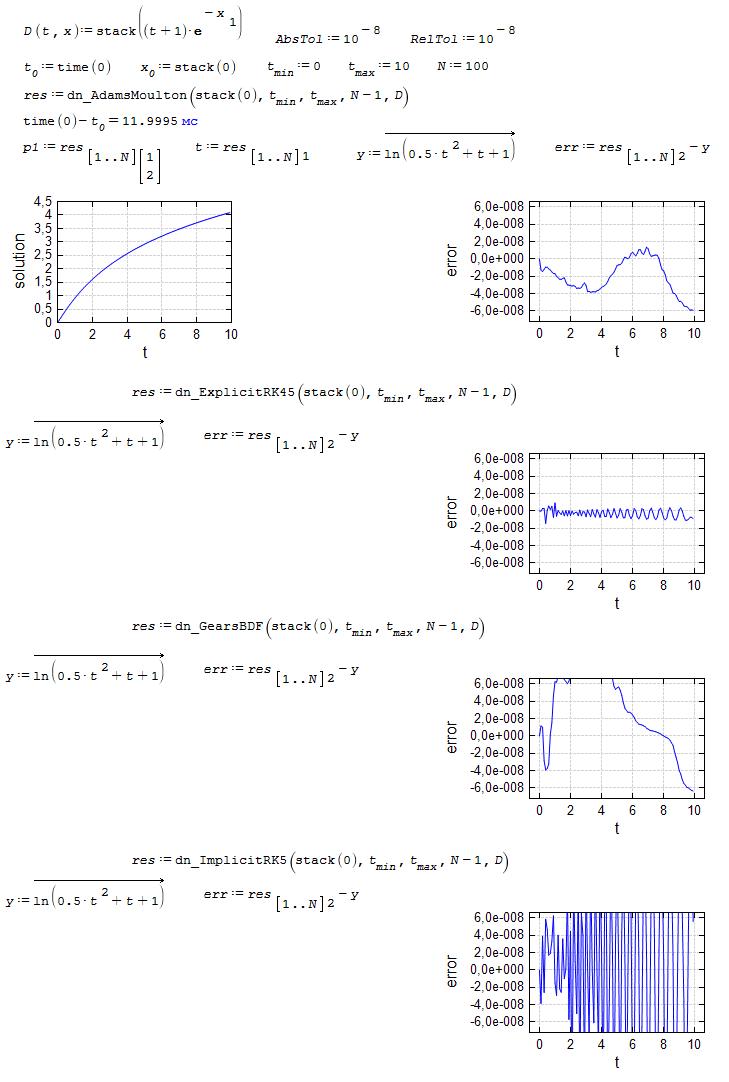
It seems that all the dotnumeric ode solver functions fail to add the last step to the solution. In the given example, the exact solution is (approximately) met if the end value of x is increased by one step (x_end/steps).

The sheet is easily extended to whatever ode solvers by adding their name to the search list. The actually available solvers depend on what plugins are installed.

Section Math ODE precision.sm (23,66 КиБ) скачан 604 раз(а).
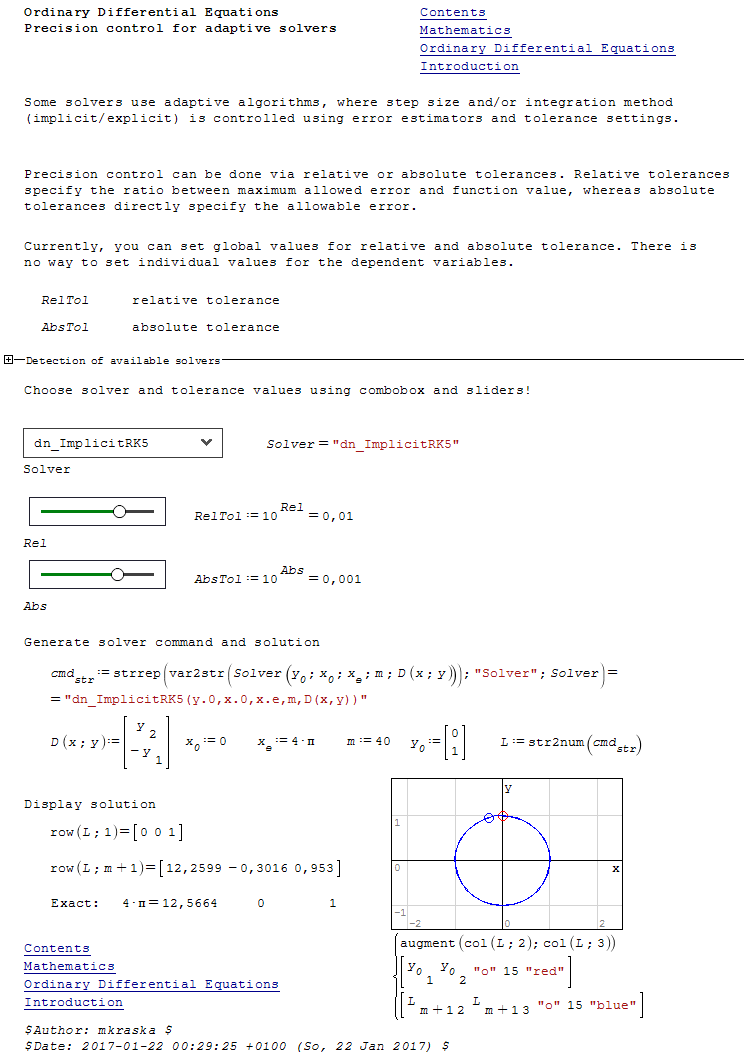
$Section Math ODE precision.png$

Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx

2 пользователям понравился этот пост

frapuano 09.09.2018 17:18:00, Вячеслав Мезенцев 10.09.2018 05:37:00

#24 Опубликовано: 10.09.2018 06:48:25

Вячеслав Мезенцев

1 518 сообщений из 1 825 понравились пользователям.

Группа: Moderator

Updated for SS 0.99.6824. Intervals issue fixed.

Russia ☭ forever, Viacheslav N. Mezentsev

3 пользователям понравился этот пост

sergio 10.09.2018 07:02:00, frapuano 10.09.2018 09:23:00, NDTM Amarasekera 10.09.2018 09:48:00

#25 Опубликовано: 06.12.2018 14:42:53

Вячеслав Мезенцев

1 518 сообщений из 1 825 понравились пользователям.

Группа: Moderator

Updated.

Changes:
- zero point issue fixed;
- added support for the simple D(t,x) definition.

Russia ☭ forever, Viacheslav N. Mezentsev

#26 Опубликовано: 24.12.2018 09:13:53

Вячеслав Мезенцев

1 518 сообщений из 1 825 понравились пользователям.

Группа: Moderator

Updated.

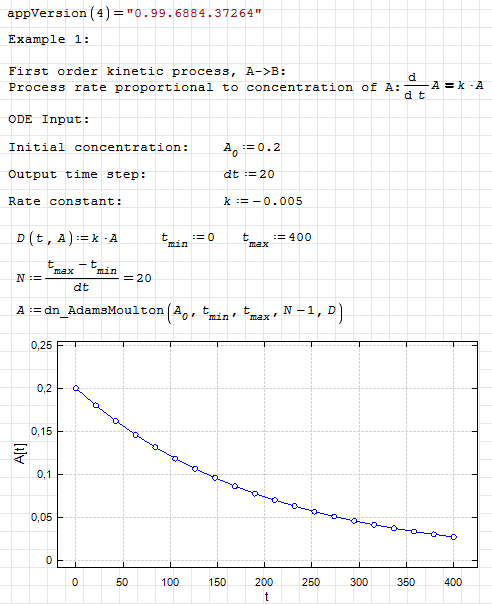
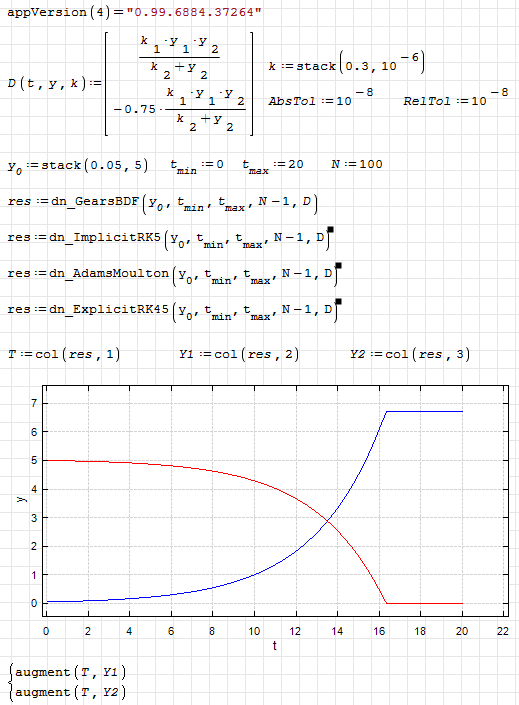
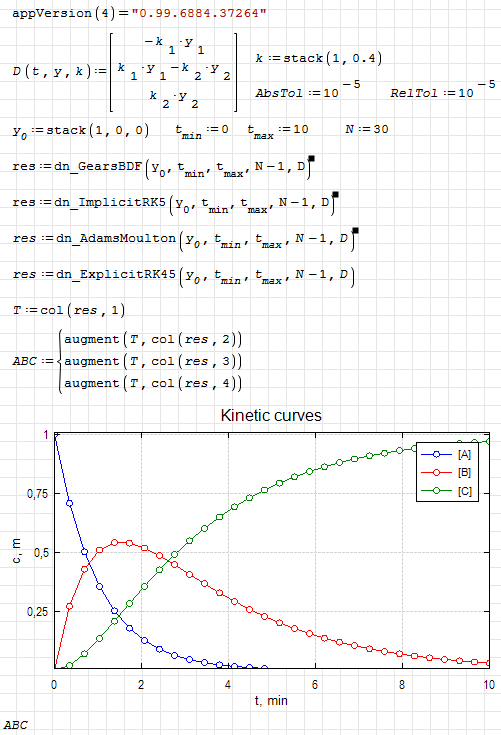
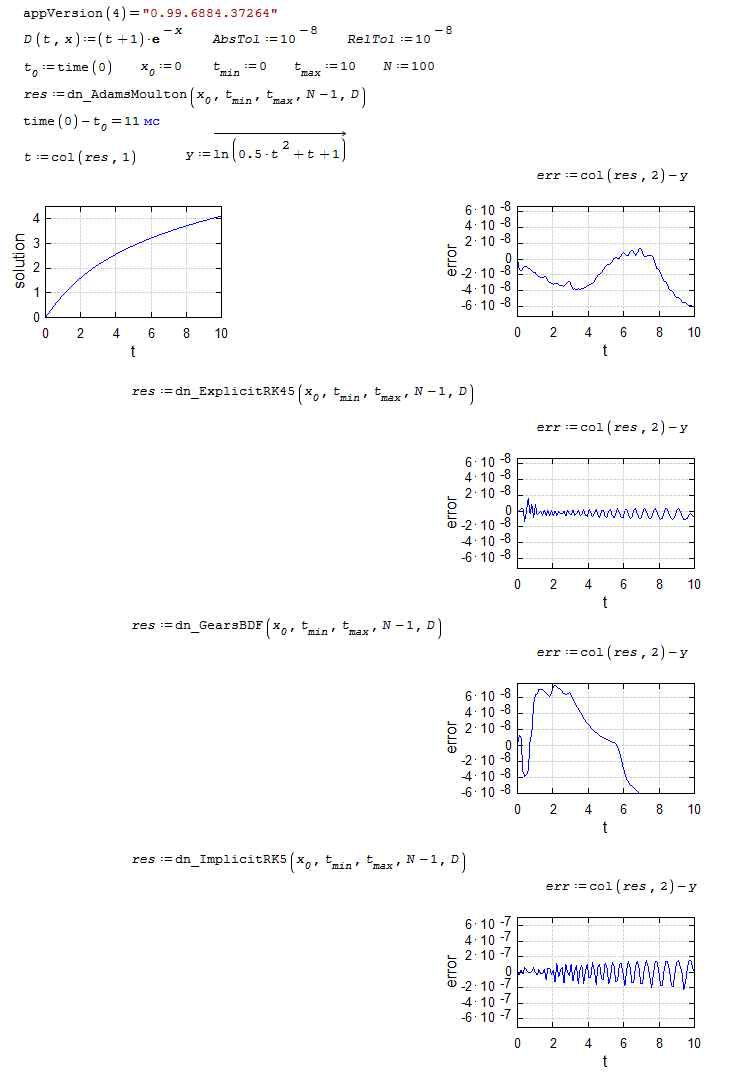
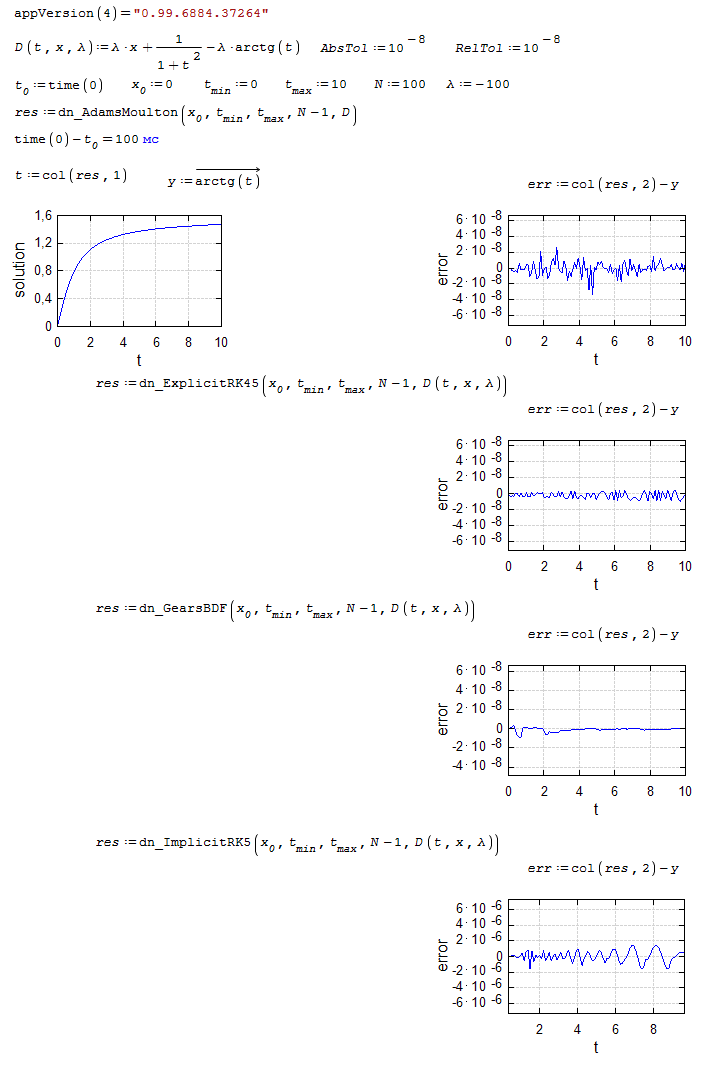
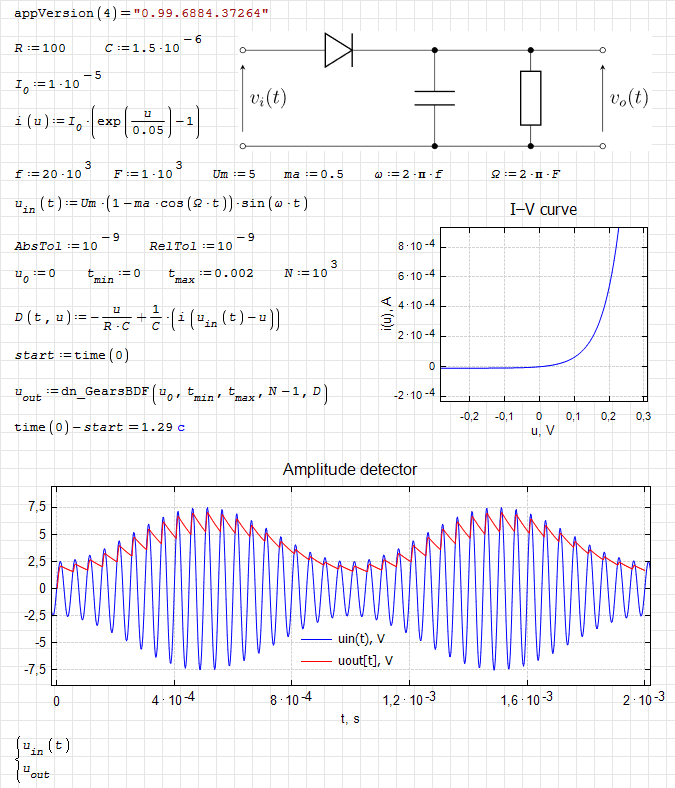
dn.ode.kinetic1.sm (8,26 КиБ) скачан 666 раз(а).
dn.ode.kinetic2.sm (12,59 КиБ) скачан 617 раз(а).
dn.ode.kinetic3.sm (12,28 КиБ) скачан 619 раз(а).
dn.ode.test1.sm (19,58 КиБ) скачан 634 раз(а).
dn.ode.test2.sm (18,88 КиБ) скачан 629 раз(а).
dn.ode.Amplitude detector.sm (20,17 КиБ) скачан 644 раз(а).

dn.ode.kinetic1.pdf (77,42 КиБ) скачан 418 раз(а).
dn.ode.kinetic2.pdf (93,05 КиБ) скачан 399 раз(а).
dn.ode.kinetic3.pdf (91,31 КиБ) скачан 384 раз(а).
dn.ode.test1.pdf (115,72 КиБ) скачан 391 раз(а).
dn.ode.test2.pdf (120,44 КиБ) скачан 381 раз(а).
dn.ode.Amplitude detector.pdf (148,87 КиБ) скачан 379 раз(а).

Russia ☭ forever, Viacheslav N. Mezentsev

4 пользователям понравился этот пост

NDTM Amarasekera 24.12.2018 09:44:00, sergio 24.12.2018 11:04:00, frapuano 24.12.2018 14:23:00, Radovan Omorjan 24.12.2018 14:52:00

#27 Опубликовано: 25.12.2018 14:49:08

Jean Giraud

983 сообщений из 6 866 понравились пользователям.

Группа: User

Native works as well.
You can try rkfixedSteven.

#28 Опубликовано: 25.12.2018 16:25:11

Jean Giraud

983 сообщений из 6 866 понравились пользователям.

Группа: User

Read + interesting stuff.

Chemical Kinetics: Introduction with Mathcad/Maple/MCS. Chapter 3

1 пользователям понравился этот пост

frapuano 25.12.2018 19:01:00

#29 Опубликовано: 09.12.2021 09:10:25

Вячеслав Мезенцев

1 518 сообщений из 1 825 понравились пользователям.

Группа: Moderator

Plugin updated.

Changes:

- added support the mathematical form of the problem for ODE solvers;
- refactored.

Russia ☭ forever, Viacheslav N. Mezentsev

1 пользователям понравился этот пост

sergio 09.12.2021 11:40:00

#30 Опубликовано: 20.12.2021 16:18:13

Вячеслав Мезенцев

1 518 сообщений из 1 825 понравились пользователям.

Группа: Moderator

Plugin updated.

Changes:

- solution restructured;
- converting the task for the ODE solver to the numerical form is now performed through the Mathcad Toolbox plugin (to avoid code duplication), so it must be installed;
- refactored.

Solvers that support mathematical notation now reuse code from the Mathcad Toolbox plugin. Now there is no need to recompile every such plugin.

Russia ☭ forever, Viacheslav N. Mezentsev

#31 Опубликовано: 21.08.2022 02:43:28

Alvaro Diaz Falconi

1 054 сообщений из 1 719 понравились пользователям.

Группа: User

Hi Viacheslav. There are an issue with Implicit and dn_ExplicitRK45, just in the first element. Please see the attached.

dn_ExplicitRK45 issue.sm (8,42 КиБ) скачан 521 раз(а).

Best regards.
Alvaro.

1 пользователям понравился этот пост

Вячеслав Мезенцев 22.08.2022 03:11:00

#32 Опубликовано: 22.08.2022 03:12:45

Вячеслав Мезенцев

1 518 сообщений из 1 825 понравились пользователям.

Группа: Moderator

Plugin updated.

Changes:

- fixed values of initial conditions in the output array for dn_ImplicitRK5() and dn_ExplicitRK45().

Russia ☭ forever, Viacheslav N. Mezentsev

2 пользователям понравился этот пост

sergio 22.08.2022 04:19:00, Alvaro Diaz Falconi 23.08.2022 20:15:00

Форум SMath

DotNumerics - Initial-value problem for nonstiff and stiff ordinary differential equations ODEs - Сообщения