DotNumerics - Initial-value problem for nonstiff and stiff ordinary differential equations ODEs - Сообщения





Functions list:
dn_AdamsMoulton(4) - (ode,y(x),xmax,steps) uses the Adams-Moulton method.
dn_AdamsMoulton(5) - (ics,xmin,xmax,steps,D(x,y)) uses the Adams-Moulton method.
dn_ExplicitRK45(3) - (ode,y(x),xmax) uses the explicit Runge-Kutta (4)5 method.
dn_ExplicitRK45(4) - (ode,y(x),xmax,steps) uses the explicit Runge-Kutta (4)5 method.
dn_ExplicitRK45(5) - (ics,xmin,xmax,steps,D(x,y)) uses the explicit Runge-Kutta (4)5 method.
dn_GearsBDF(3) - (ode,y(x),xmax) uses the Gear’s BDF method.
dn_GearsBDF(4) - (ode,y(x),xmax,steps) uses the Gear’s BDF method.
dn_GearsBDF(5) - (ics,xmin,xmax,steps,D(x,y)) uses the Gear’s BDF method.
dn_ImplicitRK5(3) - (ode,y(x),xmax) uses the implicit Runge-Kutta 5 method.
dn_ImplicitRK5(4) - (ode,y(x),xmax,steps) uses the implicit Runge-Kutta 5 method.
dn_ImplicitRK5(5) - (ics,xmin,xmax,steps,D(x,y)) uses the implicit Runge-Kutta 5 method.
dn_LinAlgEigenvalues(1) - ( A ) computes the eigenvalues of a square matrix (general, symmetric, symmetric band and complex general matrices).
dn_LinAlgEigenvectors(1) - ( A ) computes the eigenvectors of a square matrix (general, symmetric, symmetric band and complex general matrices).
dn_LinAlgLLS_COF(2) - ( A, B ) computes the minimum-norm solution to a real linear least squares problem. Using a omplete orthogonal factorization of A.
dn_LinAlgLLS_QRorLQ(2) - ( A, B ) computes the minimum-norm solution to a real linear least squares problem. Using a QR or LQ factorization of A.
dn_LinAlgLLS_SVD(2) - ( A, B ) computes the minimum-norm solution to a real linear least squares problem. Using the singular value decomposition of A.
dn_LinAlgSolve(2) - ( A, B ) computes the solution to a real system of linear equations (general, band and tridiagonal matrices): A * X = B.
dn_LinAlgSVD(1) - ( A ) computes the singular value decomposition (SVD) of a real M-by-N matrix: A = U * S * transpose(V).
dn_MatrixInverse(1) - ( A ) calculate the inverse matrix.
Differential Equations. Initial-value problem for nonstiff and stiff ordinary differential equations ODEs (explicit Runge-Kutta, implicit Runge-Kutta, Gear’s BDF and Adams-Moulton).
Solvers for Non-Stiff Systems:
dn_AdamsMoulton(init, x1, x2, intvls, D) solves an initial-value problem for nonstiff ordinary differential equations using the Adams-Moulton method.
dn_ExplicitRK45(init, x1, x2, intvls, D) solves an initial-value problem for nonstiff ordinary differential equations using the explicit Runge-Kutta method of order (4)5.
Solvers for Stiff Systems:
dn_ImplicitRK5(init, x1, x2, intvls, D) solves an initial-value problem for stiff ordinary differential equations using the implicit Runge-Kutta method of order 5.
dn_GearsBDF(init, x1, x2, intvls, D) solves an initial-value problem for stiff ordinary differential equations using the Gear’s BDF method.
Arguments:
- init is either a vector of n real initial values, where n is the number of unknowns (or a single scalar initial value, in the case of a single ODE).
- x1 and x2 are real, scalar endpoints of the interval over which the solution to the ODE(s) is evaluated. Initial values in init are the values of the ODE function(s) evaluated at x1.
- intvls is the integer number of discretization intervals used to interpolate the solution function. The number of solution points is the number of intervals + 1.
- D is a vector function of the form D(x,y) specifying the right-hand side of the system
Options:
- AbsTol - absolute tolerance parameter, default value 10⁻⁷.
- RelTol - relative tolerance parameter, default value 10⁻⁴.
Links:
1. DotNumerics is a website dedicated to numerical computing for .NET. DotNumerics includes a Numerical Library for .NET. The library is written in pure C# and has more than 100,000 lines of code with the most advanced algorithms for Linear Algebra, Differential Equations and Optimization problems. The Linear Algebra library includes CSLapack, CSBlas and CSEispack, these libraries are the translation from Fortran to C# of LAPACK, BLAS and EISPACK, respectively.
2. Arenstorf orbit. Numerical Analysis: Theory and Applications. Proseminar, 28.03.2011, UIBK [pdf].
3. How to find spatial periodic orbits around the Moon in the TBP.
Books:
1. Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems.
Examples:
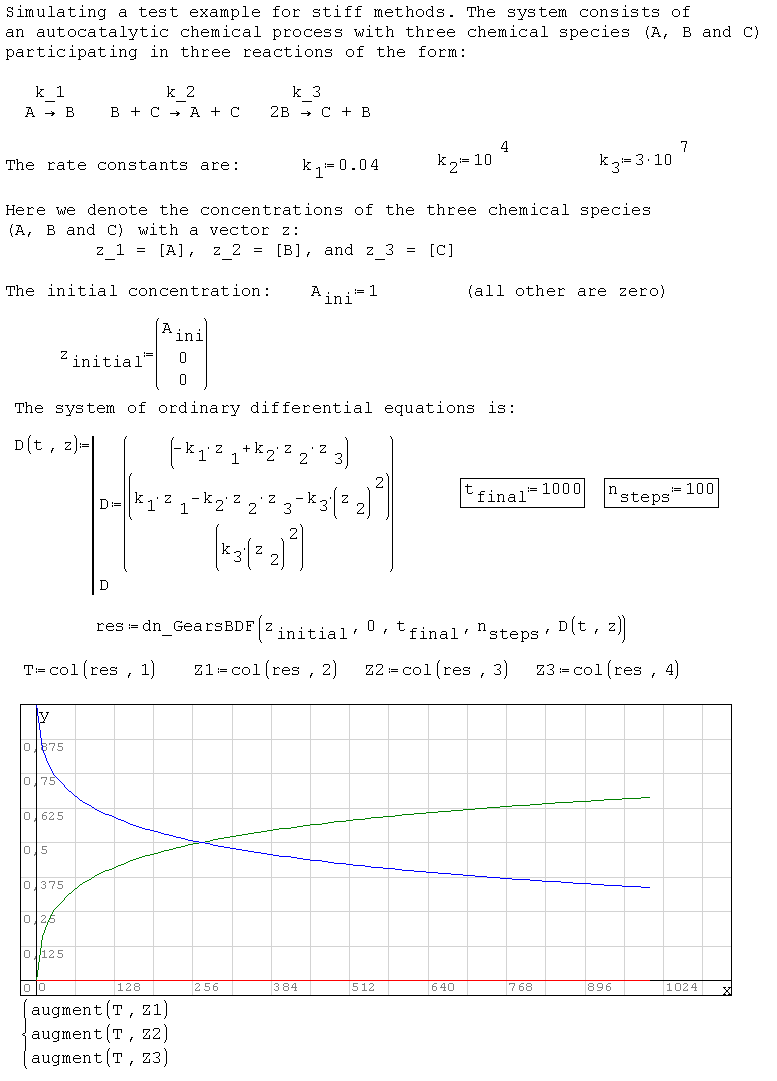
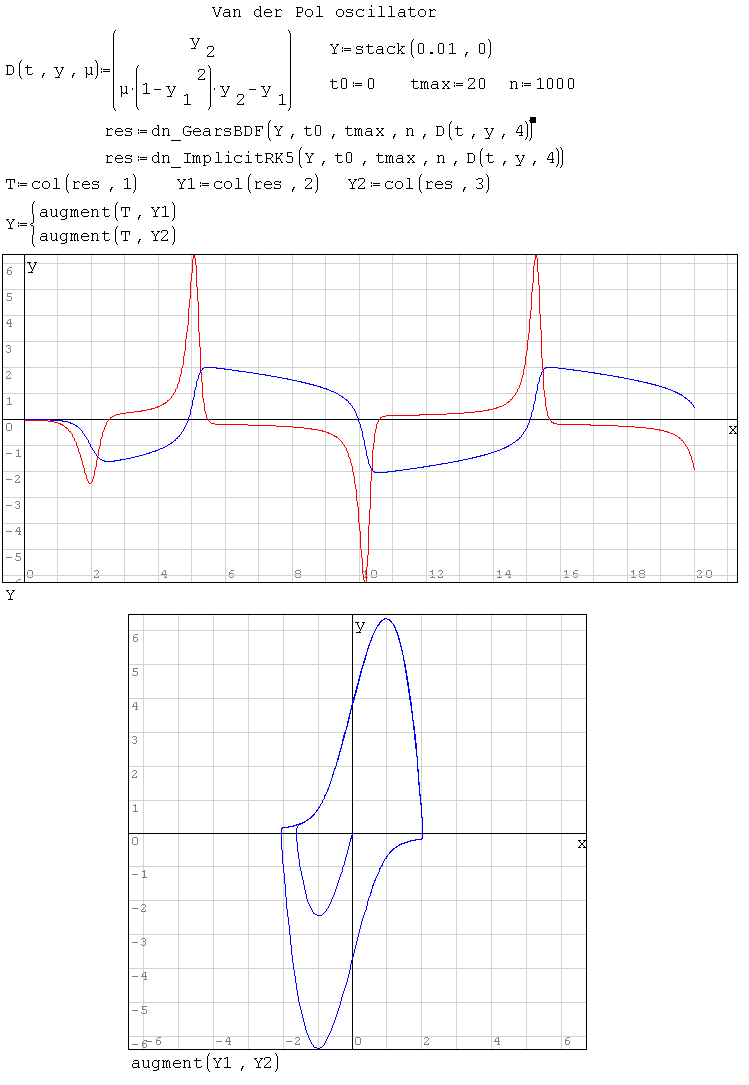
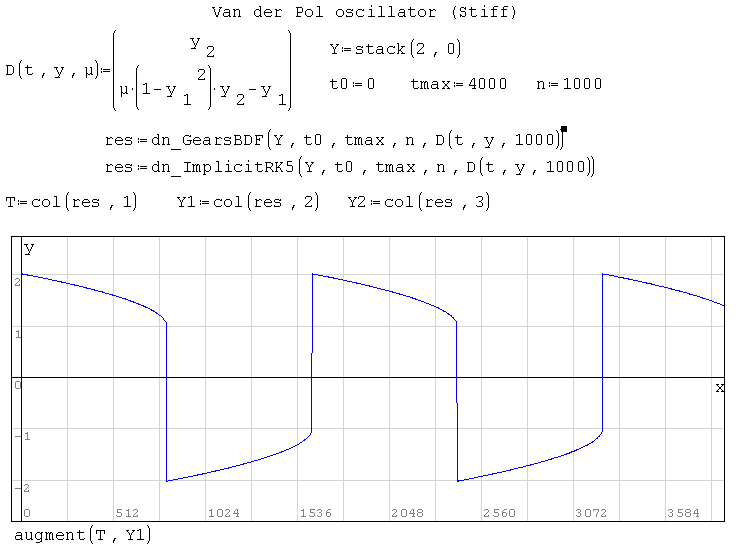
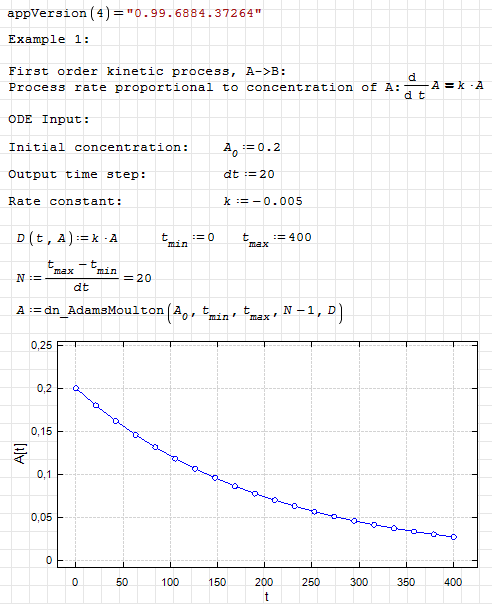
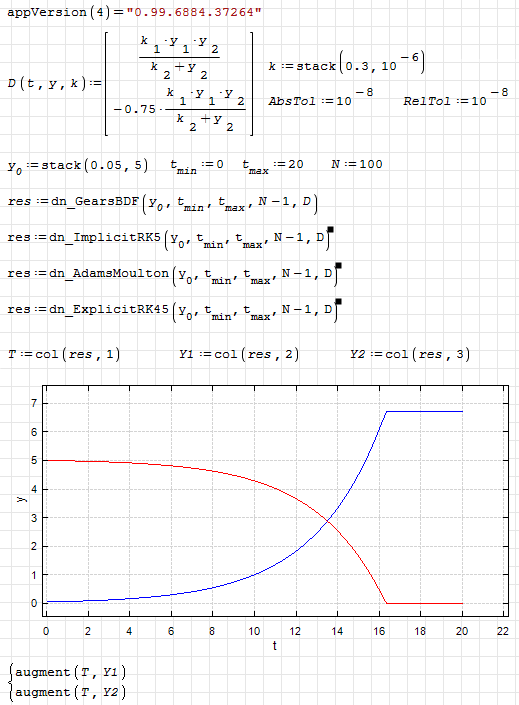
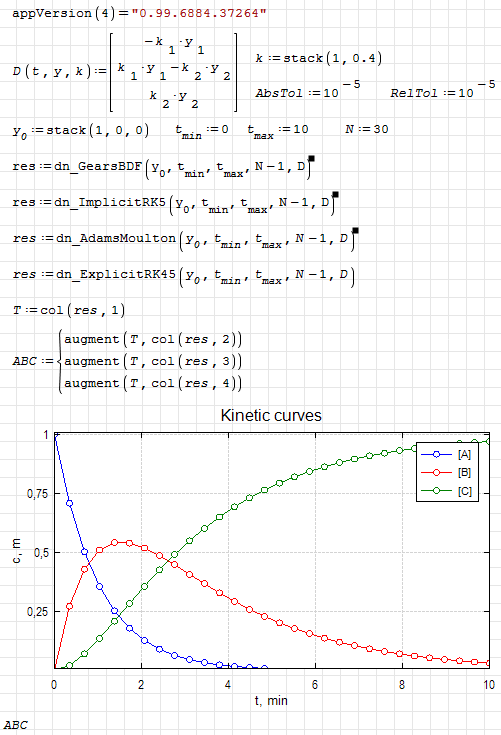
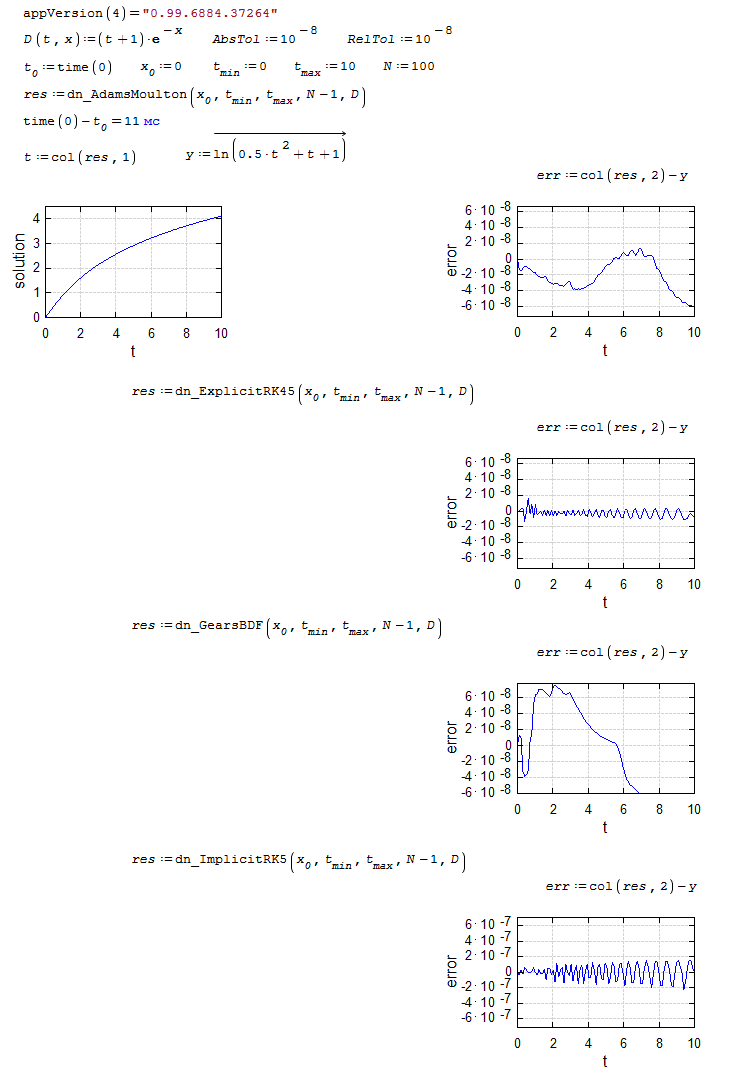
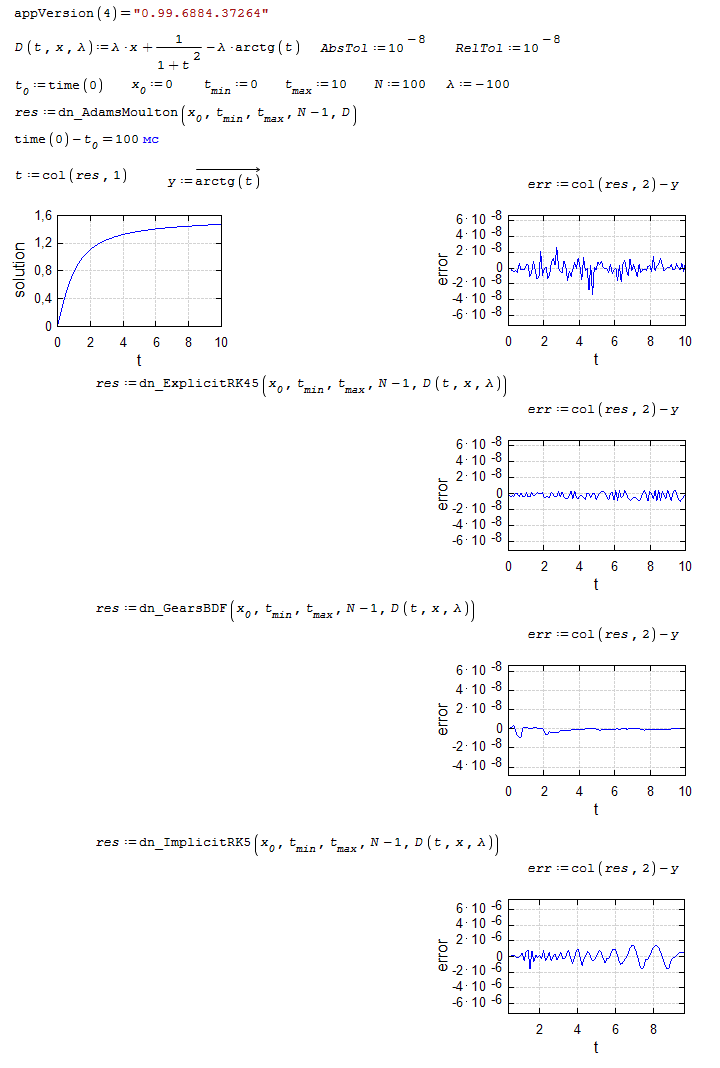
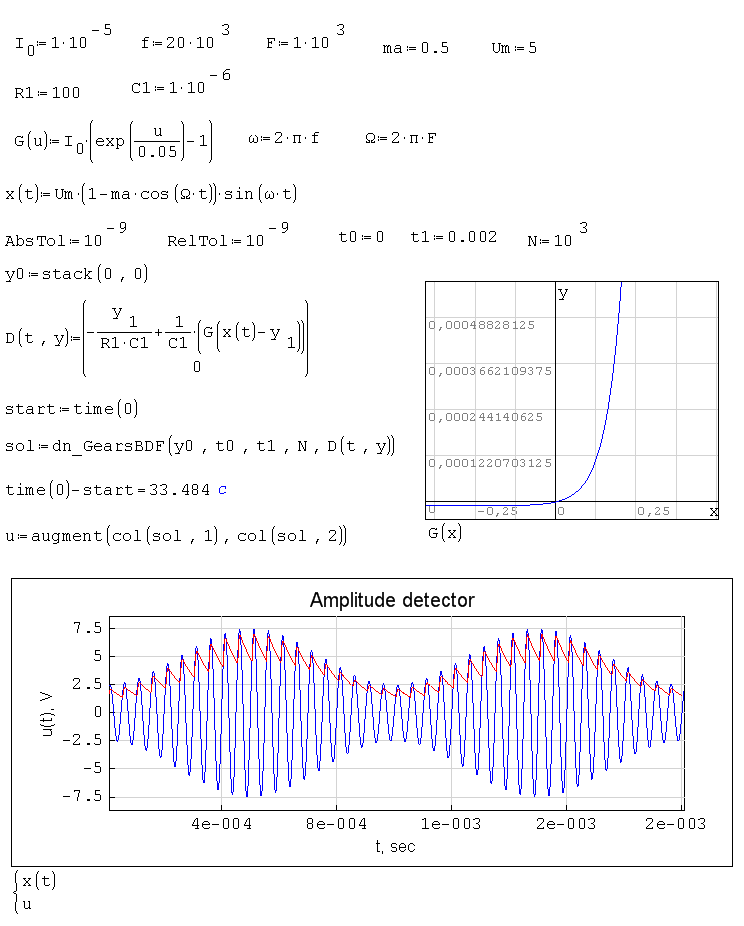
dn.ode.kinetic1.sm (8,26 КиБ) скачан 1101 раз(а).
dn.ode.kinetic2.sm (12,59 КиБ) скачан 1047 раз(а).
dn.ode.kinetic3.sm (12,28 КиБ) скачан 1043 раз(а).
dn.ode.test1.sm (19,58 КиБ) скачан 1050 раз(а).
dn.ode.test2.sm (18,88 КиБ) скачан 1062 раз(а).
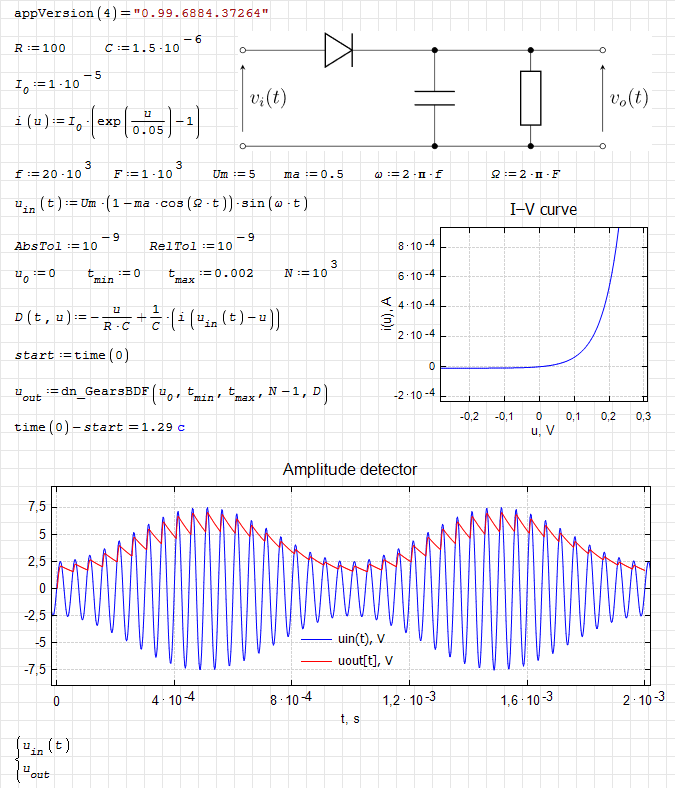
dn.ode.Amplitude detector.sm (20,17 КиБ) скачан 1057 раз(а).
dn.ode.kinetic1.pdf (77,42 КиБ) скачан 557 раз(а).
dn.ode.kinetic2.pdf (93,05 КиБ) скачан 546 раз(а).
dn.ode.kinetic3.pdf (91,31 КиБ) скачан 531 раз(а).
dn.ode.test1.pdf (115,72 КиБ) скачан 539 раз(а).
dn.ode.test2.pdf (120,44 КиБ) скачан 530 раз(а).
dn.ode.Amplitude detector.pdf (148,87 КиБ) скачан 531 раз(а).
See also:
● [topic=726]Mathcad Toolbox[/topic]
● [topic=13809]SADEL[/topic]
● [topic=1970]Matlab C++ Math Library[/topic]
● [topic=17063]OSLO[/topic]
● [topic=17067]lsoda[/topic]
● [topic=1997]GNU Scientific Library (GSL)[/topic]
DorNumerics. ODE. Arenstorf orbit.sm (91,95 КиБ) скачан 1006 раз(а).
WroteThank you uni,

dn_GearsBDF might be the ODE solver of choice for SMath. I would not mind some more solvers as well
Regards,
Radovan
Updated. dn_AdamsMoulton(), dn_ExplicitRK45(), dn_ImplicitRK5() added.
In Russia we say: получите, распишитесь.
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
If you are by any chance here on Thassos-Greece (I am here with my family on the vacation) just let me know and come for a beer
Regards,
Radovan
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
I am just curious how is the numerical accuracy controlled in all your solvers? There is no any additional parameter about this, or I was wrong about it?.
Regards,
Radovan
WroteYou're a lucky man, on Greek island with beer and I'm in Siberia with the bears

WroteBy the way uni,
I am just curious how is the numerical accuracy controlled in all your solvers? There is no any additional parameter about this, or I was wrong about it?.
Regards,
Radovan
For all methods the following values:
RelTol = 1.0E-4,
AbsTol = 1.0E-7
I will add the ability to change it. I think, using variables in the document: RelTol and AbsTol.
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
WroteWroteYou're a lucky man, on Greek island with beer and I'm in Siberia with the bears





Just imagine how different we are?. My "Lord of the ring" bring us here - me and our children, and I am most interested to "chat" here with you about the ODE solvers
Regards,
Radovan
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
WroteWroteBy the way uni,
I am just curious how is the numerical accuracy controlled in all your solvers? There is no any additional parameter about this, or I was wrong about it?.
Regards,
Radovan
For all methods the following values:
RelTol = 1.0E-4,
AbsTol = 1.0E-7
I will add the ability to change it. I think, using variables in the document: RelTol and AbsTol.
I must be annoying now
Regards,
Radovan
WroteWroteWroteBy the way uni,
I am just curious how is the numerical accuracy controlled in all your solvers? There is no any additional parameter about this, or I was wrong about it?.
Regards,
Radovan
For all methods the following values:
RelTol = 1.0E-4,
AbsTol = 1.0E-7
I will add the ability to change it. I think, using variables in the document: RelTol and AbsTol.
I must be annoying now, but could you try please try to reduce this numbers just a bit and try my "famous" example with bioreactions. I used recently some ODE stiff solvers from a package inside R. They gave the same results with negative concentration. Then, I reduced the default values for the accuracy and it worked a bit longer, but gave me the expected zero concentration.
Regards,
Radovan
Updated. I've added support for accuracy (not completely). The library allows to set accuracy for each equation separately. Now for all the equations will be the same accuracy.
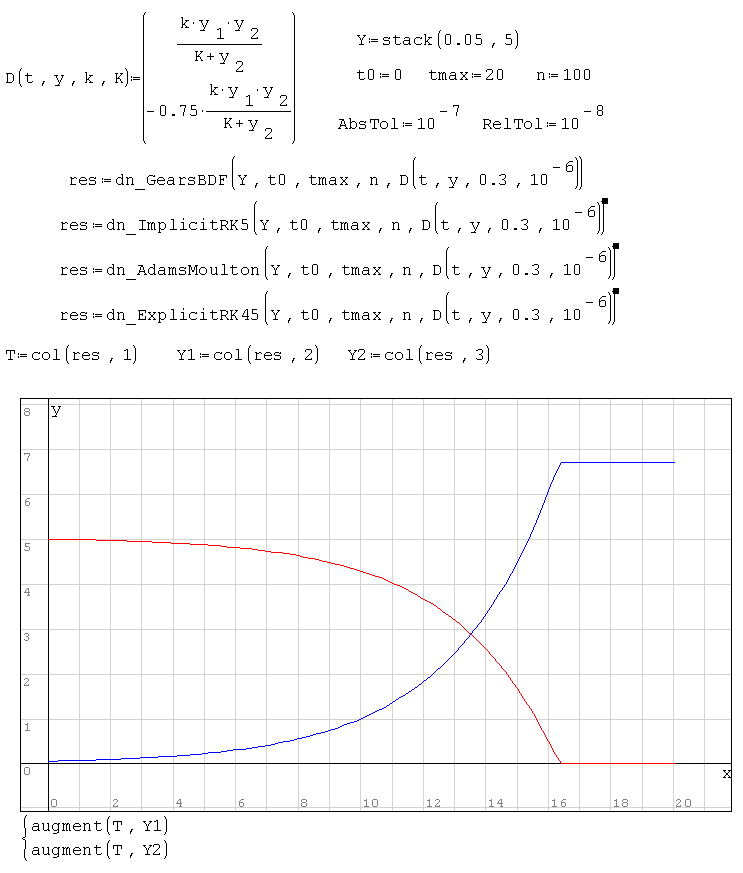
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
WroteWroteWroteWroteBy the way uni,
I am just curious how is the numerical accuracy controlled in all your solvers? There is no any additional parameter about this, or I was wrong about it?.
Regards,
Radovan
For all methods the following values:
RelTol = 1.0E-4,
AbsTol = 1.0E-7
I will add the ability to change it. I think, using variables in the document: RelTol and AbsTol.
I must be annoying now, but could you try please try to reduce this numbers just a bit and try my "famous" example with bioreactions. I used recently some ODE stiff solvers from a package inside R. They gave the same results with negative concentration. Then, I reduced the default values for the accuracy and it worked a bit longer, but gave me the expected zero concentration.
Regards,
Radovan
Updated. I've added support for accuracy (not completely). The library allows to set accuracy for each equation separately. Now for all the equations will be the same accuracy.
Yes ...
WroteHi Uni,
I've seen you can play the magician and make people's dreams to come true.
I have such a modest dream – ta have available in SMath some others modules from DOTNUMERICS, particularly the EISPACK one.
If my gentle request is not too abusive, please let me know how to address this package.
Please accept my wishes for an agreeable summer.
The same greetings for all the forum members and particularly to Andrey!
Ioan
Well, if that's possible, I'll do it. Thank you.
[+]: dn_LinAlgSolve(), dn_LinAlgLLS_COF(), dn_LinAlgLLS_QRorLQ(), dn_LinAlgLLS_SVD(), dn_LinAlgSVD(), dn_LinAlgEigenvalues(), dn_LinAlgEigenvectors(), dn_MatrixInverse().
ЦитатаI have such a modest dream – ta have available in SMath some others modules from DOTNUMERICS, particularly the EISPACK one.
What kind of functions do you need?
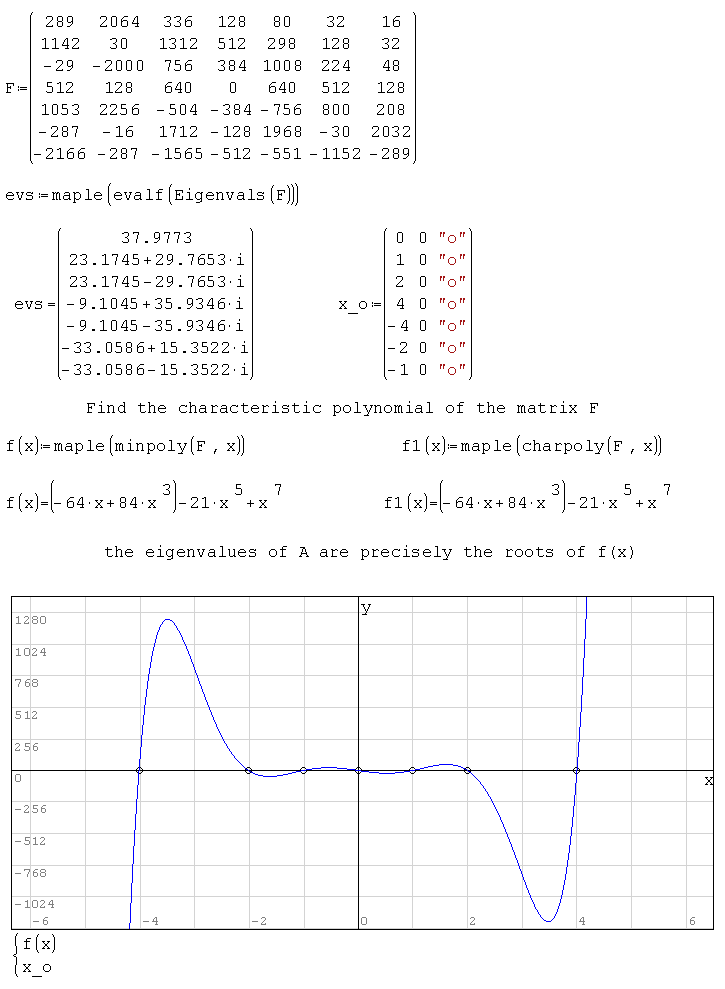
I'm not sure that dn_LinAlgEigenvalues() works correctly.
DotNumerics. Linear Algebra. Example 1.sm (28,95 КиБ) скачан 969 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
I played a bit with your example. It seems to me that eigenvalues and eigenvectors are correct for both matrices A and F. For the matrice F you gave the vector of eigenvalues which should be correct ("must be" vector). It seems that both vectors of eigenvalues - this one and the one found by dn_LinAlgEigenvalues() correspond to the eigenvectors fond by dn_LinAlgEigenvectors(). I am not sure this should be all right then or some numerical "glitch" is involved here. For some simpler matrices it works Ok and we can get the desired result by simple transformations of eigenvectors. I do not know how the AlgLib works and which kind of transformtion uses in order to give one of the many possible solutions for eigenvectors. I might be wrong about all of this, of course.
This time again eval() must be used as well to get the result. Moreover, again the well known annoying thing that sometimes the results with and without eval() are slightly different. See the attached file please.
Regards,
Radovan
DotNumerics_LinearAlgebra_Example-corr.sm (106,57 КиБ) скачан 938 раз(а).
DotNumerics. Linear Algebra. Example 2.sm (11,82 КиБ) скачан 989 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
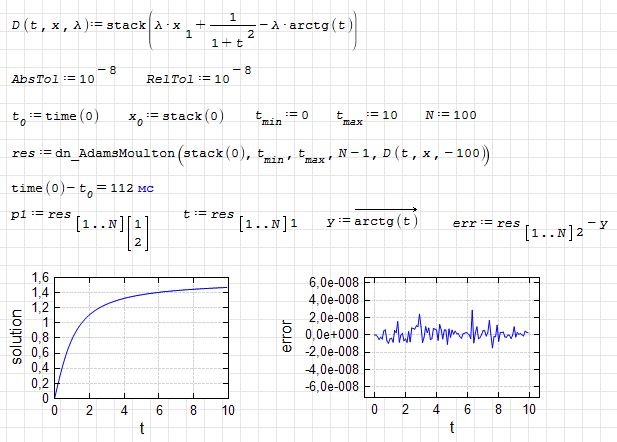
dn_AdamsMoulton.test1.sm (11,33 КиБ) скачан 937 раз(а).
dn_AdamsMoulton.test1.pdf (48,2 КиБ) скачан 436 раз(а).
- Новые сообщения
- Нет новых сообщений