NonlinearSolvers plugin - BDQRF, Bisection, Brent's, Broyden's, Newton-Raphson, Ridder's, Secant, Homotopy - Сообщения
Wrote@Alvaro
Do you think these methods based on bisection could be useful for multivariate non-linear systems ?
Hi kilele. I have not enough experience solving nonlinear systems to help you in this question. What can I say it's that bisection "method" have the degree of theorem (called Bolzano), and this is the reason for what is very powerfull. Another point is that you can evaluate the time previously of a call of the solver, as is pointed in your first cited paper (in the conclusions).
And "always is there", this is, if you are implementing some method,can test some conditions for "go by the sure" and use bisection. For example, in "Algorithms for Minimization Without Derivatives" by Richard Brent, choose bisection or interpolation if (abs(c) < toler) + (abs(fa) <= abs(fb))
Regards.
Alvaro.
http://goo.gl/SfTOK
Edit:
I've found the algorithm in fortran for the generalized version I linked above:
paper
fortran code
Hi all,
in the attached plugin:
- new function LevenbergMarquardt(...) - Levenberg-Marquardt optimization algorithm
- new function Hessian(...) - 2nd order derivatives
- All root-finding algorithms in k variable now accept multiple thresholds (a target precision value for each function)
- Fixed "custom decimal symbol" issue of HRE functions.
NOTES:
- Hessian() generates 2nd order derivatives or Hessians depending on the type of arguments.
PLEASE REPORT ANY ISSUE
best regards,
w3b5urf3r
P.S. minimization/optimization useful references:
http://en.wikipedia.org/wiki/Levenberg%E2%80%93Marquardt_algorithm
http://www2.imm.dtu.dk/pubdb/views/edoc_download.php/3215/pdf/imm3215.pdf
http://www.brnt.eu/phd/node10.html
http://www.it-weise.de/projects/book.pdf
P.P.S. @omorr or @uni I had trouble posting directly this message, there are likely 5 or 6 equal post in background.
Hessian_testing.sm (19,22 КиБ) скачан 891 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
I could see you are close to realizing the optimization (minimization/maximization) algorithms as well
Of course, derivatives would cause problems sometimes, and it would be quite useful if they could be avoided.
WroteP.P.S. @omorr or @uni I had trouble posting directly this message, there are likely 5 or 6 equal post in background.
I do not know what can we do about it. I suppose it is a SPAM filter of the Forum issue. Your unfinished versions of this post appeared in the unapproved posts.
If someone else experienced this, just let us know.
Regards,
Radovan
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
WroteI've seen you're example, unfortunately there are many little "issues" regarding the symbolic engine...
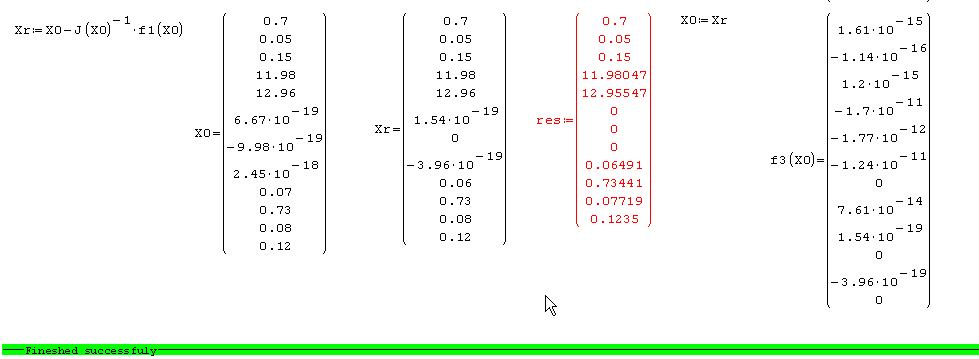
For example observes the first element of your f1(), f2() and f3() (look the attachments);
f1()
SMath seem unable to make a symbolical stack of the function; It's not difficult to understand why... the columns of the results matrix (if all it's correct) are the columns of the last stack argument -> 1; the rows are undefined because if [MATH lang=eng]el(X#,2)[/MATH],[MATH lang=eng]el(X#,4)[/MATH],[MATH lang=eng]el(X#,5)[/MATH] and [MATH lang=eng]el(X#,3)[/MATH] are vectors, the result is a vector... exluding the assumption that all unknown elements are numbers or a "size predeclaring", probably the issue could be solved using a "trial and error" procedure on the unknown size, but I think it's a very hard task
f2()
Here there are SMath issues with derivatives... probably it's the same issue of f3() (and the same of this bug), IMHO all related to the symbolic simplification engine...
f3()
Here there are SMath issues with derivatives and elements...
Since all the issues with derivatives involving the Jacobian, so NewtonRaphson(), HRE.NR() and HRE.RK() in this example can not be used (at the moment, at least)
Here we go again with this @nightmare@ example. If we can not use Jacobian (Smath can'not calculate them from neither of f1(),f2(),f3() functions) - let's try a numerically found one (calculated by my rather simple function Jacnum()). It seems it is working very well with this "driving me crazy" example and using quite bad initial guess and few simple NewtonRaphson with this numerically Jacobian ( Quasi-Quasi-NR-Omorr method
See the attached example.
By the way, I would suggest you to consider using numerically found Jacobian in Levenberg-Marquardt method as well.
Regards,
Radovan
Hi all,
in the attached plugin:
- new function GaussNewton(...) - Gauss-Newton optimization algorithm.
- new functions GoldenSectionSearch.min(...) and GoldenSectionSearch.max(...) - Golden Section Search minimization/maximization algorithms.
- new functions GradientDescent(...) and GradientDescent.GSS(...) - Gradient Descent optimization algorithm (respectively with fixed step length and GoldenSectionSearch-based step length).
- new functions NewtonMethod(...) and NewtonMethod.GSS(...) - Newton Method optimization algorithm (respectively with fixed step length and GoldenSectionSearch-based step length).
- new function Gradient(...) - 1st order derivatives.
- new function Diag(...) - improved SMath diag().
- function Jacobian(...) revisited (now returns only a derivative or a mxn Jacobian)
- solver Bisection(...) revisited (the number of iterations is no longer required, as reported by adiaz)
from previous BETA
- new function LevenbergMarquardt(...) - Levenberg-Marquardt optimization algorithm (previous BETA - fixed issues)
- new function Hessian(...) - 2nd order derivatives (previous BETA - no changes)
- All root-finding algorithms in k variable now accept multiple thresholds (a target precision value for each function) (previous BETA - no changes)
- Fixed "custom decimal symbol" issue of HRE functions. (previous BETA - no changes)
SEE THE ATTACHMENTS FOR ALL DETAILS - PLEASE REPORT ANY ISSUE
WroteHello w3b5urf3r,
Here we go again with this @nightmare@ example. If we can not use Jacobian (Smath can'not calculate them from neither of f1(),f2(),f3() functions) - let's try a numerically found one (calculated by my rather simple function Jacnum()). It seems it is working very well with this "driving me crazy" example and using quite bad initial guess and few simple NewtonRaphson with this numerically Jacobian ( Quasi-Quasi-NR-Omorr method)
See the attached example.
By the way, I would suggest you to use consider using numerically found Jacobian in Levenberg-Marquardt method as well.
Regards,
Radovan
I'm considering it, BTW i hope the issue on differentiation order it will be solved ASAP :d .
best regards,
w3b5urf3r
BETA_testing sm files.zip (24,57 КиБ) скачан 285 раз(а).
all test files worked, except for GoldenSectionSearch due to the issue with custom delimiter settings (pops up whenever there are dots in the function names in plugins).
BTW, the function desciptions appear twice in the Plugins dialog.
Best regards, Martin Kraska
WroteGreat work!
all test files worked, except for GoldenSectionSearch due to the issue with custom delimiter settings (pops up whenever there are dots in the function names in plugins).
Best regards, Martin Kraska
Thank you Martin, the "empty stack" issue it's a SMath bug related to the reference function name (now renamed, see the attachments)
BTW I've reuploaded both plugin and examples, with minor changes.
WroteBTW, the function desciptions appear twice in the Plugins dialog.
The 2nd description appear when a function have "optional arguments"; indeed there is a boolean parameter to hide the description, but in the dynamic assistance description only; I don't know how (and if there is a way) to hide the second description in the plugin window (however I think it's a feature, not a bug).
best regards,
w3b5urf3r
delimiters_bug.sm (1,32 КиБ) скачан 857 раз(а).
Jacobian Computation-free Newton’s Method for Systems of Nonlinear Equations: http://jnmas.org/jnmas2-5.pdf
regards,
w3b5urf3r
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
My congratulations for your efforts. Yo have all my respect for that
But...I must be annoying with nagging so many times about Jacobian, Gradient, Hessian analytically
This is (again
I would kindly ask you just to try, when you have the time, to replace all those derivative dependent things wit some numerical complement. Regarding all those troubles with derivatives, I do not see any other way in order to get out from this very common problem like Nonlinear least squares. I tried to chage your LevenberMarquartd.ref() function and to replace Jacobian() and Gradient() with the numerical ones without success. Gradient() gave me troubles that I could not resolve - Just made it from my Jacnum() function, but it did not work.
Regards,
Radovan
http://www.alglib.net/optimization/levenbergmarquardt.php
Read on from the section "Getting started with Levenberg-Marquardt", it seems this algorithm needs analytic Jacobian for achieving high performance or high accuracy.
Newton-Raphson with finite diferences pages 10-11-12
http://dmaii.etsii.upm.es/~IngElec/downloads/Clase_sisno_2_06.pdf
Levenberg–Marquardt with finite diferences page 33
http://www.jldelafuenteoconnor.es/Clase_mincua_nolineal_12.pdf
Hybrid method: Levenberg-Marquardt + Quasi-Newton(Broyden-Fletcher-Goldfarb-Shanno)
Matlab code page 81
http://riunet.upv.es/bitstream/handle/10251/10343/memoria.pdf
EDIT:
The last document contains 4 methods of least squares written in matlab
(analytic:fast but only for canonical/regular problems; numeric: flexible for many problems but memory/time consuming; hybrid: combines the latter ones)
There are also approximations for Jacobian and Gradient on page 84.
Wrote
BTW I've reuploaded both plugin and examples, with minor changes.
The 2nd description appear when a function have "optional arguments"; indeed there is a boolean parameter to hide the description, but in the dynamic assistance description only; I don't know how (and if there is a way) to hide the second description in the plugin window (however I think it's a feature, not a bug).
Hi, I just downloaded testfiles and plugin from post #86 and still get the empty stack message with GoldenSectionSearch_testing.sm.
As to the function list in the plugin manager: I forgot that smath treats same names with different numbers of args as different functions. Thus the apparently same entries are not really identical. Perhaps ordering by name would make that more obvious.
Now some even less important issue:
In the function descriptions, the german translation of the argument names is somewhat odd. Lower and upper bounds ("delimiter" ) appear as "Trennzeichen", meaning "delimiting character" just as dec and arg delimiter. I guess you do not have much choice as to how choose names for the arguments. Even if that might be less descriptive, it would perhaps be more safe to use "variable".
Best regards, Martin
WroteHi, I just downloaded testfiles and plugin from post #86 and still get the empty stack message with GoldenSectionSearch_testing.sm.
Thank you, please try again with the new "BETA_testing sm files.zip", I've forgot to replace the ";" in two reference functions.
WroteAs to the function list in the plugin manager: I forgot that smath treats same names with different numbers of args as different functions. Thus the apparently same entries are not really identical. Perhaps ordering by name would make that more obvious.
Now some even less important issue:
In the function descriptions, the german translation of the argument names is somewhat odd. Lower and upper bounds ("delimiter" ) appear as "Trennzeichen", meaning "delimiting character" just as dec and arg delimiter. I guess you do not have much choice as to how choose names for the arguments. Even if that might be less descriptive, it would perhaps be more safe to use "variable".
Best regards, Martin
No problem, I'll do it in the next relase.
regards,
w3b5urf3r
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
WroteHope this can be of any help ^^
Newton-Raphson with finite diferences pages 10-11-12
http://dmaii.etsii.upm.es/~IngElec/downloads/Clase_sisno_2_06.pdf
Levenberg–Marquardt with finite diferences page 33
http://www.jldelafuenteoconnor.es/Clase_mincua_nolineal_12.pdf
Hybrid method: Levenberg-Marquardt + Quasi-Newton(Broyden-Fletcher-Goldfarb-Shanno)
Matlab code page 81
http://riunet.upv.es/bitstream/handle/10251/10343/memoria.pdf
EDIT:
The last document contains 4 methods of least squares written in matlab
(analytic:fast but only for canonical/regular problems; numeric: flexible for many problems but memory/time consuming; hybrid: combines the latter ones)
There are also approximations for Jacobian and Gradient on page 84.
Numerical derivatives, Jacobian, Gradient, Hessian must be sometimes used sooner or later - in spite of their numerical drawbacks.
By the way, I mentioned the following issue few times. You can use cinterp() or ainterp() to obtain a spline interpolation from a tabulated two dimensional data and to find a spline function. But you can not have the derivatives of that function. One of the main reason to use the interpolation methods is to make a continuous function from data which can be then differentiated and integrated - in SMath the derivatives of this spline function can not be obtained at the moment.
Regards,
Radovan
P.S. Mathcad is using a variation of Ridder's method for finding derivatives numerically.
http://riunet.upv.es/bitstream/handle/10251/10343/memoria.pdf
that it assumes the function has first and second derivatives and both are continue, otherwise the conditions to calculate the minimum change and so do the algorithms to apply, in that case the author invites the reader to consult:
"Roger Fletcher. Practical Methods of Optimization. John Wiley & Sons, 2001"
Wrote
Thank you, please try again with the new "BETA_testing sm files.zip", I've forgot to replace the ";" in two reference functions.Wrote
Now some even less important issue:
In the function descriptions, the german translation of the argument names is somewhat odd. Lower and upper bounds ("delimiter" ) appear as "Trennzeichen", meaning "delimiting character" just as dec and arg delimiter. I guess you do not have much choice as to how choose names for the arguments. Even if that might be less descriptive, it would perhaps be more safe to use "variable".
Best regards, Martin
No problem, I'll do it in the next relase.
Hi,
no empty stack messages any more, thank you. Also thanks for not disregarding my superficial feedback.
Best regards, Martin
Hi omorr,WroteHello w3b5urf3r,
My congratulations for your efforts. Yo have all my respect for that.
But...I must be annoying with nagging so many times about Jacobian, Gradient, Hessian analytically. I become to like the sentence "Jacobian Computation-free" as in your previous post.
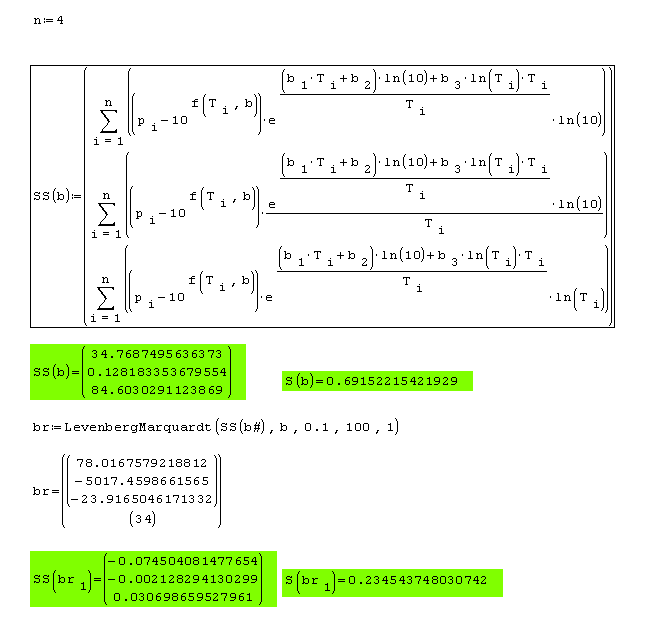
This is (again) my Nonlinear least square test problem. I tried it with LevenberMarquartd(). As might be expected, almost impossible to solve it - large expression and problems with derivatives
. I reduced the number of points (n=4) and the LM gave the result. One might try, but it should take more than an hour to get the result. Just wanted to check if this is working. It is working, but that slow and almost useless it this case.
I would kindly ask you just to try, when you have the time, to replace all those derivative dependent things wit some numerical complement. Regarding all those troubles with derivatives, I do not see any other way in order to get out from this very common problem like Nonlinear least squares. I tried to chage your LevenberMarquartd.ref() function and to replace Jacobian() and Gradient() with the numerical ones without success. Gradient() gave me troubles that I could not resolve - Just made it from my Jacnum() function, but it did not work.
Regards,
Radovan
Seems that the computation efforts are in the Jacobian calculation... BTW I'm implementing Central Differences Gradient/Jacobian/Hessian (in the attachment a test with your primer_47w
In the attachment a sm file containing the algorithm above... works, but not as expectedWroteAn interesting algorithm

Jacobian Computation-free Newton’s Method for Systems of Nonlinear Equations: http://jnmas.org/jnmas2-5.pdf
regards,
w3b5urf3r
regards,
w3b5urf3r
JCFN.sm (24,03 КиБ) скачан 831 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
WroteSeems that the computation efforts are in the Jacobian calculation... BTW I'm implementing Central Differences Gradient/Jacobian/Hessian (in the attachment a test with your primer_47w
)
Thank you very much and I am very grateful to you
I'm looking forward to it and really hope that this will improve the situation, although the step size is critical here. When you have the time, could you please consider something like Ridder's method I've mentioned. As I understood, the derivatives are calculated with some larger step and decreased afterwards. Something like described here - Ridder's method.
WroteJacobian Computation-free Newton’s Method for Systems of Nonlinear Equations: http://jnmas.org/jnmas2-5.pdf
...In the attachment a sm file containing the algorithm above... works, but not as expected
It looks quite simple and promising. Therefore, If I would have it available I'll always give it a try first.
Regards,
Radovan
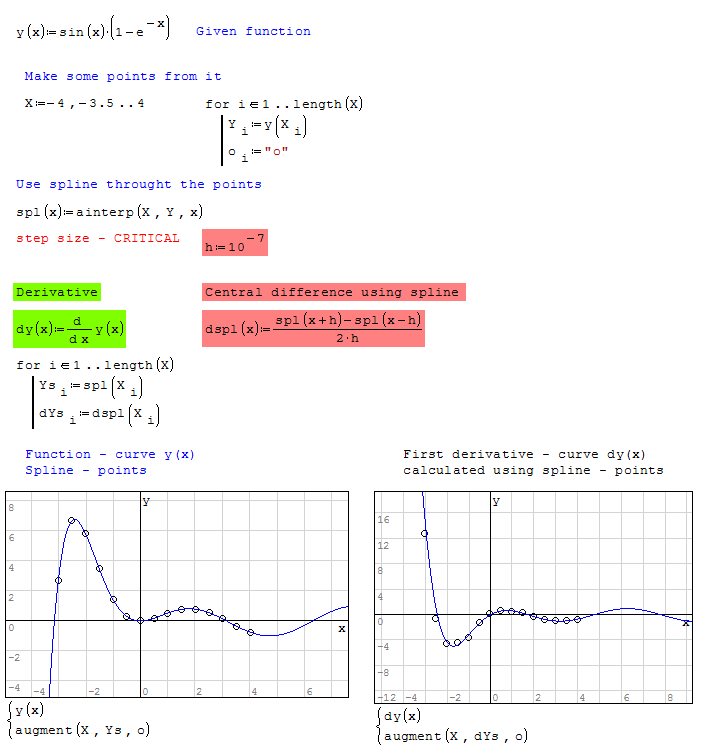
I did some simple testing, here are the results.
The screenshot is generated with standard settings for dec and arg delims.
Broyden and HRE.B generate errors with non-standard settings (dec , and arg
Quite interesting that solve(4) outperforms them all in the given example.
Most solvers that take intervals as arguments just allow one root in that interval.
Best regards, Martin
trig.sm (18,93 КиБ) скачан 893 раз(а).
- Новые сообщения
- Нет новых сообщений
