NonlinearSolvers plugin - BDQRF, Bisection, Brent's, Broyden's, Newton-Raphson, Ridder's, Secant, Homotopy - Сообщения
WroteHi,
I did some simple testing, here are the results.
The screenshot is generated with standard settings for dec and arg delims.
Broyden and HRE.B generate errors with non-standard settings (dec , and arg. All other errors seem not to be custom settings related.
Quite interesting that solve(4) outperforms them all in the given example.
Most solvers that take intervals as arguments just allow one root in that interval.
Best regards, Martin
Thank you again Martin
see the attachment, the issues are fixed with the plugin in the following post.
regards,
w3b5urf3r

Hi all,
in the attached plugin:
- new functions NCGM(...) and NCGM.CD(...) - Nonlinear conjugate gradient method optimization algorithms;
- new function Gradient.CD(...) - central differences based Gradient;
- new function Jacobian.CD(...) - central differences based Jacobian;
- new function Hessian.CD(...) - central differences based Hessian;
- new functions GaussNewton.CD(...) and GaussNewton.CDGSS(...) - central differences based GaussNewton;
- new function LevenbergMarquardt.CD(...) - central differences based LevenbergMarquardt;
- new function NewtonRaphson.CD(...) - central differences based NewtonRaphson;
- new functions NewtonMethod.CD(...) and NewtonMethod.CDGSS(...) - central differences based NewtonMethod;
- increased performances on Gradient/Jacobian/Hessian-based functions;
- fixed issues of Broyden(...) and HRE.B(...) about custom settings;
- minor changes.
from previous BETA:
- new function GaussNewton(...) - Gauss-Newton optimization algorithm (previous BETA - increased performances);
- new functions GoldenSectionSearch.min(...) and GoldenSectionSearch.max(...) - Golden Section Search minimization/maximization algorithms (previous BETA - no changes);
- new functions GradientDescent(...) and GradientDescent.GSS(...) - Gradient Descent optimization algorithm (respectively with fixed step length and GoldenSectionSearch-based step length) (previous BETA - increased performances);
- new function LevenbergMarquardt(...) - Levenberg-Marquardt optimization algorithm (previous BETA - increased performances);
- new functions NewtonMethod(...) and NewtonMethod.GSS(...) - Newton Method optimization algorithm (respectively with fixed step length and GoldenSectionSearch-based step length) (previous BETA - increased performances);
- new function Diag(...) - improved SMath diag() (previous BETA - no changes);
- new function Gradient(...) - 1st order derivatives (previous BETA - increased performances);
- new function Hessian(...) - 2nd order derivatives (previous BETA - increased performances);
- function Jacobian(...) revisited (now returns only a derivative or a mxn Jacobian) (previous BETA - increased performances);
- solver Bisection(...) revisited (the number of iterations is no longer required, as reported by adiaz) (previous BETA - no changes);
- All root-finding algorithms in k variable now accept multiple thresholds (a target precision value for each function) (previous BETA - no changes);
- Fixed "custom decimal symbol" issue of HRE functions. (previous BETA - no changes);
REQUIRES customFunctions plugin
SEE THE ATTACHMENTS FOR MANY INFOS - PLEASE REPORT ANY ISSUE
best regards,
w3b5urf3r
BETA_testing sm files.zip (31,85 КиБ) скачан 321 раз(а).
thank you for the instant response. I confirm the points mentioned in your screenshot of post #101. Special thanks for your patience with custom settings. This aspect must be really annoying for those who use standard settings. I am insisting because I an teaching to german engineering students who are supposed to respect DIN standards.
In your HRE.RK example you used a precision with ° unit. That makes me wonder if I got the precision argument usage right. Is it a tolerance to the functions or to the variables? Both could be sensible convergence criteria. A given variable tolerance might be sensible if you solve for the displacements of a mechanical system based on equillibrium conditions. You might be satisfied with being within 1mm from the solution regardless how big the residual forces are.
I did some timing and convergence testing, see attachments. The results are a little surprising.
Best regards, Martin
trig1.sm (16,29 КиБ) скачан 919 раз(а).
WroteHi w3b5urf3r,
thank you for the instant response. I confirm the points mentioned in your screenshot of post #101. Special thanks for your patience with custom settings. This aspect must be really annoying for those who use standard settings. I am insisting because I an teaching to german engineering students who are supposed to respect DIN standards.
In your HRE.RK example you used a precision with ° unit. That makes me wonder if I got the precision argument usage right. Is it a tolerance to the functions or to the variables? Both could be sensible convergence criteria. A given variable tolerance might be sensible if you solve for the displacements of a mechanical system based on equillibrium conditions. You might be satisfied with being within 1mm from the solution regardless how big the residual forces are.
I did some timing and convergence testing, see attachments. The results are a little surprising.
Best regards, Martin
Hi Martin,
No problem, regional settings it's an important feature of SMath and I want the plugin give less problems as possible.
In all the root finding methods the convergence it's set with reference to the function value: [MATH lang=eng]f(x.target)
Bracketed algorithms accept a 2nd convergence criterion on bracket width, further convergence criteria will be added ASAP.
Please be careful with homotopy estimation methods... the 4th arguments represents the homotopy transformations ([MATH lang=eng]Δλ
regards,
w3b5urf3r
Wrote
Bracketed algorithms accept a 2nd convergence criterion on bracket width, further convergence criteria will be added ASAP.
Please be careful with homotopy estimation methods... the 4th arguments represents the homotopy transformations ([MATH lang=eng]Δλ1-0)/homotopyTransformations[/MATH]); any transformation involve a root-finding call, so more tranformations->more calls->most computation time; considere that 10 transformations (or less) are usually enough.
Hi w3b5urf3r,
thanks again. I played around with the bracketed root finding algorithms based on your Bisection test file. The precision argument is either a number or a two element list, each element being again a number. I guess/propose that in further releases these elements might be lists, giving tolerances for the individual functions (first list) and for the variables (second list). Secant() is complaining about type of arguments.
The flexibility of your functions in terms of how the system is formatted and the mechanism of identifying the unknowns is really impressive and highly welcome.
BTW: How can I remove definitions from the namespace, i.e. make previously defined names unknown?
My surprise with the HRE test was not so much about the high computation time of HRE.NR but in that increasing a non-eaten-up maximum changes the number of required iteration.
The ordinary user dreams of a wrapper function that by some logic uses whatever solver might be appropriate. A brute force approach would be to try all available variants with increasing number of allowed iterations, perhaps with some sort of trace protocol such that could gain some experience by playing around.
Best regards, Martin
Bisections_testing_Kr.sm (61,44 КиБ) скачан 880 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
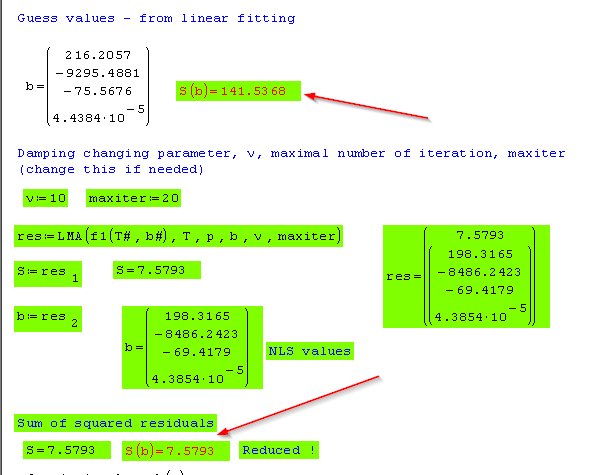
I was playing a bit with optimization .CD functions - of course with my "famous" NLS example. The calculation time decreases on some more acceptable level (order of magnitude - few minutes each) and I could afford more runs for this testing. It seems that for this example the best performance had GausNewton.CD, NewtonMethod.CD and NewtonMethod.CDGSS. Morover, NewtonMethod.CDGSS performed the best (with a bit longer calculation time) - just compare with the result obtained by my LMA() function in the same file. I was expecting much more from LevenbergMarquardt() - to be quite good at this example, but it seems I was wrong. It was quite slow and rather inefficient. Actually, CD functions did some quite good job compared to the original ones. Hope that some more improvements could be done here
The attached are two files (worse and better initial conditions).
The picture is for the worse ones.
Regards,
Radovan

325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
Here is another attempt, with the same problem but now directly minimizing the following standard sum of squared residuals - function S(x,y,z):
[MATH=eng]S(x,y,z):sum(((el(p,i)-10^{x+y/el(T,i)+z*log(el(T,i),10)})^2),i,1,n)[/MATH]
Again, it seems that NewtonMethod.CDGSS() performed the best for this example. Here are two files with better and worse initial conditions. The picture represented solutions with better initial conditions. I tried with different number of points (reduced the variable n in front of the function S(x,y,z) and the situation seems to be similar. NewtonMethod.CDGSS() was the best.
Those functions are promising requiring less computational time and hope that this testing and examples could give you some ideas how to increase the performance of those functions
Regards,
Radovan

325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
It seems you've done something with the numerical derivatives - it seems quite accurate
Just for comparison see the post and the picture above regarding spline and spline derivatives . Jacobian.CD() - Gradient.CD() did the job quite well
Thank you very much
Regards,
Radovan
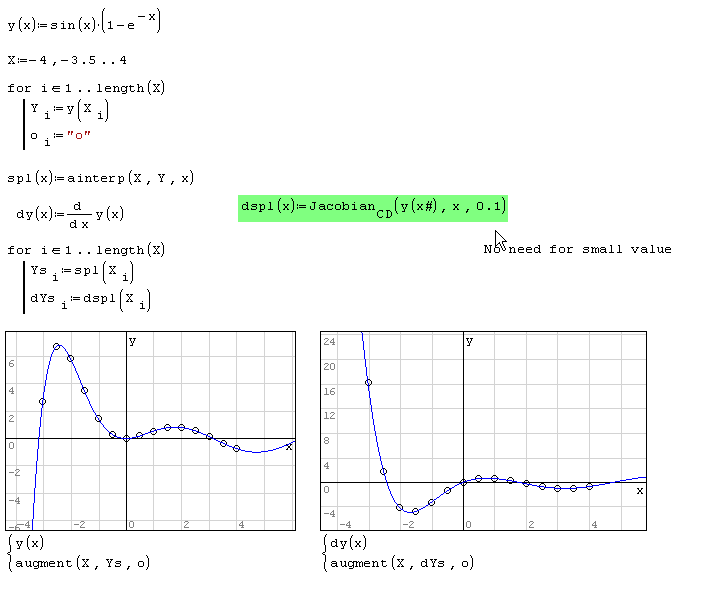
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
Instead of minimizing sum of squared residuals, I've tried now to use individual residuals in order to minimize them, that will sometimes work (Levenberg Marquard should do the job here). It appeared that it worked well and quite fast for most of the methods
On the other hand, the squared residuals minimization is represented in files *8.sm and *8a.sm. It also worked quite well
Regards,
Radovan
P.S. It seems that NewtonRaphson.CD() is something wrong. I could not solve my test problem properly, as I was expected based on the previous post regarding numerical Jacobian. On the other hand, in your test file, NewtonRaphson() solved the problem in 7 iteration but NewtonRaphson.CD() solved the same problem in 344 iteration ?

WroteHello w3b5urf3r
Instead of minimizing sum of squared residuals, I've tried now to use individual residuals in order to minimize them, that will sometimes work (Levenberg Marquard should do the job here). It appeared that it worked well and quite fast for most of the methods. See the attached files *7.sm and *7a.sm (better and worse guess values)
On the other hand, the squared residuals minimization is represented in files *8.sm and *8a.sm. It also worked quite well. Therefore, I am quite satisfied with these CD functions and this example solved in this way. Will see some other example next time.
Regards,
Radovan
P.S. It seems that NewtonRaphson.CD() is something wrong. I could not solve my test problem properly, as I was expected based on the previous post regarding numerical Jacobian. On the other hand, in your test file, NewtonRaphson() solved the problem in 7 iteration but NewtonRaphson.CD() solved the same problem in 344 iteration ?
Hi omorr,
thank you for your testings
You're right, the finite difference newton-raphson contains a bug, now is solved (BETA plugin updated).
EDIT Levenberg-Marquardt and Gauss-Newton general algorithms are built to work knowing both the system of equations (the residuals) and the cost function (the sum of squared residuals; the plugin calculated the sum o squares of systems inside any algorithm); the LMA(...) in your scripts accept the sum of squared residuals as input because have a custom Jacobian inside it;
GradientDescent(...), NewtonMethod(...) and NCGM(...) need only the cost function, so you can use as input what do you want.
WroteHello w3b5urf3r,
It seems you've done something with the numerical derivatives - it seems quite accurate
Just for comparison see the post and the picture above regarding spline and spline derivatives . Jacobian.CD() - Gradient.CD() did the job quite well
Thank you very much
Regards,
Radovan
I'm surprised o_o ; I've done nothing strange, just a "generalization" of Finite difference in several variables... maybe have you changed some parameter in your test (f.e. the perturbation value)?
regards,
w3b5urf3r
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
As your fan
Thank you for correcting NewtonRaphson.CD(). It seems to work and the attached is the picture from my many times mentioned "nightmare example". It solved it very well
WroteEDIT Levenberg-Marquardt and Gauss-Newton general algorithms are built to work knowing both the system of equations (the residuals) and the cost function (the sum of squared residuals; the plugin calculated the sum o squares of systems inside any algorithm); the LMA(...) in your scripts accept the sum of squared residuals as input because have a custom Jacobian inside it;
GradientDescent(...), NewtonMethod(...) and NCGM(...) need only the cost function, so you can use as input what do you want.
Thank you for the explanation of this. To be honest, I used my test example without to much thinking about the residuals, cost function - tried everything.
Here I tried CD functions with the same example with adding one parameter (there are four parameters now). Unfortunately, all of them failed - see the attached files (*9.sm used just residuals, *9a.used squared residuals, *9b.sm used sum of squared residuals (cost function)). I might make some mistake or wrong choice of perturbation parameters or tolerance. See please the bottom of every file. My "home made" LMA() function did something, reduced the value of cost function and it seems successful here - see the green regions above (the second picture attached). If I did not do anything wrong here I hope that this will also help you to further improve these functions
Regards,
Radovan
Just for your reference,
this is a LM coded in Matlab with three numerical examples to test its numerical robustness.
see "Levenberg-Marquardt method: introduction and examples" and "Levenberg-Marquardt method: m-files"
at http://www.duke.edu/~hpgavin/ce281/
And "Iterative Methods for Optimization" by C.T. Kelley has matlab codes for LM and code for numerical derivatives.
Free code at
http://www.siam.org/books/kelley/fr18/matlabcode.php
WroteHi w3b5urf3r,
thanks again. I played around with the bracketed root finding algorithms based on your Bisection test file. The precision argument is either a number or a two element list, each element being again a number. I guess/propose that in further releases these elements might be lists, giving tolerances for the individual functions (first list) and for the variables (second list). Secant() is complaining about type of arguments.
The flexibility of your functions in terms of how the system is formatted and the mechanism of identifying the unknowns is really impressive and highly welcome.
BTW: How can I remove definitions from the namespace, i.e. make previously defined names unknown?
My surprise with the HRE test was not so much about the high computation time of HRE.NR but in that increasing a non-eaten-up maximum changes the number of required iteration.
The ordinary user dreams of a wrapper function that by some logic uses whatever solver might be appropriate. A brute force approach would be to try all available variants with increasing number of allowed iterations, perhaps with some sort of trace protocol such that could gain some experience by playing around.
Best regards, Martin
Hi Martin,
Actually my idea for target precision inputs it's something like this (a table with a row for each function):
[LIVE width=402 height=156]http://smath.info/live/?file=4014[/LIVE]
About the tracing I've already thinked to use an output *.txt file or directly a 3rd output parameter (a table), I don't know what's the better way...
A bruteforce approach like the Andrey roots() and solve() would be nice (also, f.e. a built-in maximize() and minimize() function) but It's an hard task... actually the closest approach to this goal would appear to be the Draghilev's-method implemented by Uni
regards,
w3b5urf3r
Wrote
Hi Martin,
Actually my idea for target precision inputs it's something like this (a table with a row for each function):
[LIVE width=402 height=156]http://smath.info/live/?file=4014[/LIVE]
About the tracing I've already thinked to use an output *.txt file or directly a 3rd output parameter (a table), I don't know what's the better way...
Hi w3b5urf3r,
I'd prefer a list or vector of lists as format for target precision, because the number of functions does not necessarily match the number of variables. Also, giving just one value for all functions or variables would then be done by a one element list (system). Of course, this is perhaps matter of taste and as such the cook's decision.
BTW, in the past I have repeatedly applied the evolution strategy, including the version with covariance matrix adaptation. As far as I understand, this algorithm requires eigenvalues and eigenvectors of the covariance matrix to be calculated. The procedure is quite robust against noise, including inconsistent offspring selection. See CMA ES for theory and code examples.
Best regards, Martin
WroteWrote
Hi Martin,
Actually my idea for target precision inputs it's something like this (a table with a row for each function):
[LIVE width=402 height=156]http://smath.info/live/?file=4014[/LIVE]
About the tracing I've already thinked to use an output *.txt file or directly a 3rd output parameter (a table), I don't know what's the better way...
Hi w3b5urf3r,
I'd prefer a list or vector of lists as format for target precision, because the number of functions does not necessarily match the number of variables. Also, giving just one value for all functions or variables would then be done by a one element list (system). Of course, this is perhaps matter of taste and as such the cook's decision.
BTW, in the past I have repeatedly applied the evolution strategy, including the version with covariance matrix adaptation. As far as I understand, this algorithm requires eigenvalues and eigenvectors of the covariance matrix to be calculated. The procedure is quite robust against noise, including inconsistent offspring selection. See CMA ES for theory and code examples.
Best regards, Martin
Ah... yes, I did not write previously but any ε.x# should be a vector/list/matrix if the number of variables of the related function f.x# it's greater than one
regards,
w3b5urf3r
I'm working to improve the convergence criteria; at the time I found two different ways to do this (see the attachments).
I'd like to know which would be preferred in your opinion.
best regards,
w3b5urf3r
NS_options.sm (42,25 КиБ) скачан 893 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
Wrote
...I'd like to know which would be preferred in your opinion.
If you can not keep them both at the same time, just use the one which is easier for you to perform and maintain
Regards,
Radovan
I was reading about Stiff IVPs and recalled I linked a gpl .NET library.
I've just added one more resource with GEAR BDF code on that post:
http://en.smath.info/forum/yaf_postsm7971_NonlinearSolvers-plugin--root-finding-methods--optimization-algorithms.aspx#post7971
I'd prefer local settings. However, there is the danger of bloating the dynamic assistence and the function menu by multiple functions of the same name with different numbers of arguments. Do you have access to the context menu? Then some of the options might be set there, just like decimal places and exponential thresholds. That should be limited to options that just affect the display or the output verbosity.
All options that affect the result as such should be visible without digging into menus (think of the beloved symbolic/numeric obfuscation by using the same operator for both).
The context menu options could get a global defaults dialog. Is your menu access limited to Insert? I would expect such settings in the tools>Settings menu branch.
Looking forward to an new release of your plugin...
Best regards, Martin
I played around with nonlinear solvers, unfortunately without any success. At least not if units are involved.
Are the solvers supposed to work with units?
- can the unknown variables have units (given via units of limits or start point)?
- need the epsilons have units as well?
do I need to define functions or can I just give expressions as first argument?
Bisection test.sm (9,61 КиБ) скачан 879 раз(а).
- Новые сообщения
- Нет новых сообщений
