Ошибки в Handheld версии - Messages
Скачал новую версию (0.68).
Теперь при загрузке выдает ошибку с текстом "Не удается найти PInvoke DLL "user32.dll"
Мое устройство Gigabyte GSmart MW700 (Windows Mobile 6 Pro)
P.S.: версия 0.67 работала
P.P.S.: Спасибо за программу. Надеюсь, что мои замечания помогут в отладке.
Теперь при загрузке выдает ошибку с текстом "Не удается найти PInvoke DLL "user32.dll"
Мое устройство Gigabyte GSmart MW700 (Windows Mobile 6 Pro)
P.S.: версия 0.67 работала
P.P.S.: Спасибо за программу. Надеюсь, что мои замечания помогут в отладке.
Огромное спасибо. Исправил дистрибутивы Handheld версии.
Благодаря Вам успел исправить оплошность до того, как программа распространилась. Теперь можно смело загружать и устанавливать.
Благодаря Вам успел исправить оплошность до того, как программа распространилась. Теперь можно смело загружать и устанавливать.
У меня часть панелей расположена по верхнему краю экрана. Я перевел устройство в альбомный режим. Те панели, что были снизу, выровнялись по нижнему краю, а те, что были вверху, ушли вверх, было видно только их нижнюю часть. После перевода ориентации экрана в книжную панели не вернулись, остались где-то вверху 
Если не трудно, предусмотрите пожалуйста выравнивание панелей, расположенных вверху. Заранее спасибо.
Если не трудно, предусмотрите пожалуйста выравнивание панелей, расположенных вверху. Заранее спасибо.
Еще заметил сегодня при работе с программой:
если задать уравнение, не имеющее действительных корней (например, [MATH]5*x^2+x+5[/MATH]) и попытаться найти его решения, используя меню (Меню->Вычисление->Найти корни), то вылезает ошибка NullReferenceException.
P.S.: если решать с помощью функции solve, то программа корректно срабатывает.
если задать уравнение, не имеющее действительных корней (например, [MATH]5*x^2+x+5[/MATH]) и попытаться найти его решения, используя меню (Меню->Вычисление->Найти корни), то вылезает ошибка NullReferenceException.
P.S.: если решать с помощью функции solve, то программа корректно срабатывает.
QuoteПосле перевода ориентации экрана в книжную панели не вернулись
Обязательно учту это - программа будет принимать правильное решение о местоположении панелей.
Сейчас же, для того, что бы вернуть панели нужно в "Меню" >> "Панели" убрать галку с пункта меню "Помнить раскладку". В этом случае после перезапуска программы восстановятся настройки положения панелей по-умолчанию и далее всё должно работать хорошо (галку можно будет вернуть после перезапуска).
Quote...вылезает ошибка NullReferenceException
Поправлю, спасибо.
Сделал, как вы советовали. Панели вернулись. Спасибо 
Доброго времени суток всем.
Вопрос - при символьном вичислении производной от ln(x) проблем нет, а от log3X получается ноль.
Похоже на баг.
С уважнием, Иван
Вопрос - при символьном вичислении производной от ln(x) проблем нет, а от log3X получается ноль.
Похоже на баг.
С уважнием, Иван
WroteДоброго времени суток всем.
Вопрос - при символьном вичислении производной от ln(x) проблем нет, а от log3X получается ноль.
Похоже на баг.
С уважнием, Иван
Здравствуйте.
Да, это баг. В следующей версии исправим. Спасибо, что сообщили.
www.math.by
И снова здравствуйте! 
Что-то не может программа корректно посчитать сумму с коэффициентами 1/n!
А софтина, имхо, очень интересная. Первый день играюсь, жалко не было в студенческие времена.
Еще вопрос, а спецфункции какие-нибудь появятся в будущем?
Что-то не может программа корректно посчитать сумму с коэффициентами 1/n!
А софтина, имхо, очень интересная. Первый день играюсь, жалко не было в студенческие времена.
Еще вопрос, а спецфункции какие-нибудь появятся в будущем?
Jovan1977, возможность работы с выражениями типа [MATH]sum(1/{n!};n;1;5)=1,7167[/MATH] теперь возможна (с версии 0.71).
Поиск производных от логарифма произвольного основания типа [MATH]diff(log(x;3);x)—1/{x*ln(3)}[/MATH] теперь также возможен (с версии 0.71).
Добавление спецфункций, как и добаление множества других возможностей безусловно планируется в будущих версиях программы.
Поиск производных от логарифма произвольного основания типа [MATH]diff(log(x;3);x)—1/{x*ln(3)}[/MATH] теперь также возможен (с версии 0.71).
Добавление спецфункций, как и добаление множества других возможностей безусловно планируется в будущих версиях программы.
Всем доброго времени суток.
С символьным вычислением производных от логарифмов проблем не вижу, все вроде ОК.
А экспоненту в виде ряда так и не научилась считать, причем (1/n!) или (n!)^-1 - все едино. До девятого члена (n=8) все б.м. честно, а потом - танцы с бубном, на тринадцатом вообще вываливается в минуса
На двадцать пятом - деление на ноль. Надо фиксить
Удачи. Будет время - погоняю еще, проверю графики.
ЗЫ В "справочнике" - "таблица производных" - вообще какой-то сюр с буквами творится
С символьным вычислением производных от логарифмов проблем не вижу, все вроде ОК.
А экспоненту в виде ряда так и не научилась считать, причем (1/n!) или (n!)^-1 - все едино. До девятого члена (n=8) все б.м. честно, а потом - танцы с бубном, на тринадцатом вообще вываливается в минуса
На двадцать пятом - деление на ноль. Надо фиксить
Удачи. Будет время - погоняю еще, проверю графики.
ЗЫ В "справочнике" - "таблица производных" - вообще какой-то сюр с буквами творится
WroteВсем доброго времени суток.
До девятого члена (n=8) все б.м. честно, а потом - танцы с бубном, на тринадцатом вообще вываливается в минуса
На двадцать пятом - деление на ноль. Надо фиксить
Ужас! Уже сел разбираться... Спасибо.
Wrote
ЗЫ В "справочнике" - "таблица производных" - вообще какой-то сюр с буквами творится
Какие конкретно буквы Вам не нравятся?
WroteЗЫ В "справочнике" - "таблица производных" - вообще какой-то сюр с буквами творится
Исправим. Действительно получилось непонятно и не правильно
www.math.by
Ладно, удалось убедить и мою голову  Все u будут заменены на x.
Все u будут заменены на x.
Или х на u

Вообще, справочные материалы - дело тонкое. Одна лишняя буква или штрих... и два балла на экзамене обеспечены.
Вообще, справочные материалы - дело тонкое. Одна лишняя буква или штрих... и два балла на экзамене обеспечены.
Ну, как известно, "волков бояться - в лес не ходить" и "не ошибается тот, кто ничего не делает". Первым делом перед интеграцией в программу этот справочник я давал на проверку математически умным людям, которые помогли отловить несколько неточностей, а также всегда прислушивался к замечанием пользователей - ничего большего я просто не мог сделать.
Решение же вместо x в правой части этих формул (в таблице производных) записать u было целиком и полностью на моей совести, признаю - в погоне за лаконичностью сделал глупость.
Изначально я создал бумажный математический справочник из которого уже и переписывал формулы в SMath Studio. Как можно увидеть в нём найденная Вами ошибка отсутствует:

Решение же вместо x в правой части этих формул (в таблице производных) записать u было целиком и полностью на моей совести, признаю - в погоне за лаконичностью сделал глупость.
Изначально я создал бумажный математический справочник из которого уже и переписывал формулы в SMath Studio. Как можно увидеть в нём найденная Вами ошибка отсутствует:
Вечер добрый
Вот еще что нашел, правда, не знаю, баг ли.
Итак. пишем 7*х*3 - упростить - 21*х
выделяем х и - вычисления - дифференцировать - получаем.. d/dx(3*x*7)->21*x
при этом простое вычисление производной от 21*х или 7*3*х дает корректный результат.
Магия и колдовство, блин
ЗЫ Насчет ошибок - вроде, для того и сидим, чтобы отловить по максимуму. Общими-то усилиями
Вот еще что нашел, правда, не знаю, баг ли.
Итак. пишем 7*х*3 - упростить - 21*х
выделяем х и - вычисления - дифференцировать - получаем.. d/dx(3*x*7)->21*x
при этом простое вычисление производной от 21*х или 7*3*х дает корректный результат.
Магия и колдовство, блин
ЗЫ Насчет ошибок - вроде, для того и сидим, чтобы отловить по максимуму. Общими-то усилиями
Ещё раз спасибо. Идём дальше по списку 
Когда в выражении [MATH]7*x*3—21*x[/MATH] Вы выделяете x и жмёте "Дифференцировать", программа ошибочно начинает дифференцировать не правую часть, как должна была бы, а всё это выражение. За это отвечает символьный модуль, а ему сказано, "если встречаешь выражение, которое не можешь упростить, возвращай пользователю его же". Вот тут-то и выползла ошибка: модуль встретил оператор присваивания, упрощать который он не умеет и он вернул всё, что было в задании... Исправляю... (мат. справочник уже исправил - ждём следующую версию)
Когда в выражении [MATH]7*x*3—21*x[/MATH] Вы выделяете x и жмёте "Дифференцировать", программа ошибочно начинает дифференцировать не правую часть, как должна была бы, а всё это выражение. За это отвечает символьный модуль, а ему сказано, "если встречаешь выражение, которое не можешь упростить, возвращай пользователю его же". Вот тут-то и выползла ошибка: модуль встретил оператор присваивания, упрощать который он не умеет и он вернул всё, что было в задании... Исправляю... (мат. справочник уже исправил - ждём следующую версию)
Думаю, последний вопрос на сегодня
уравнение вида [MATH]x^2-25*x[/MATH]
"Найти корни" и "solve" возвращает один корень - 0.
А [MATH]x^2-x[/MATH] дает столбец [MATH](1,0)^T[/MATH]
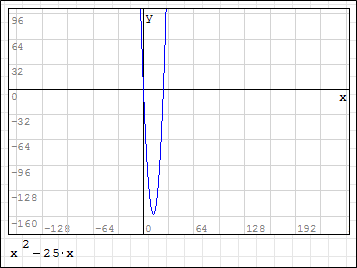
График в 2D функции [MATH]x^2-25*x[/MATH], ессно, тоже выглядит странно
уравнение вида [MATH]x^2-25*x[/MATH]
"Найти корни" и "solve" возвращает один корень - 0.
А [MATH]x^2-x[/MATH] дает столбец [MATH](1,0)^T[/MATH]
График в 2D функции [MATH]x^2-25*x[/MATH], ессно, тоже выглядит странно
Это тот редкий случай, когда ошибок нет.
Программа ищет корни численным методом, по этой причине диапазон поиска ограничен. В Handheld версии в настройках вычисления имеется возможность изменить границы поиска нулей уравнения. По этой же причине второе уравнение решается верно.
График функции выглядит верным, т.к. никак не связан с функцией solve:
Программа ищет корни численным методом, по этой причине диапазон поиска ограничен. В Handheld версии в настройках вычисления имеется возможность изменить границы поиска нулей уравнения. По этой же причине второе уравнение решается верно.
График функции выглядит верным, т.к. никак не связан с функцией solve:
- New Posts
- No New Posts
