Mathcad Toolbox - Contains analogs of functions from Mathcad - Messages
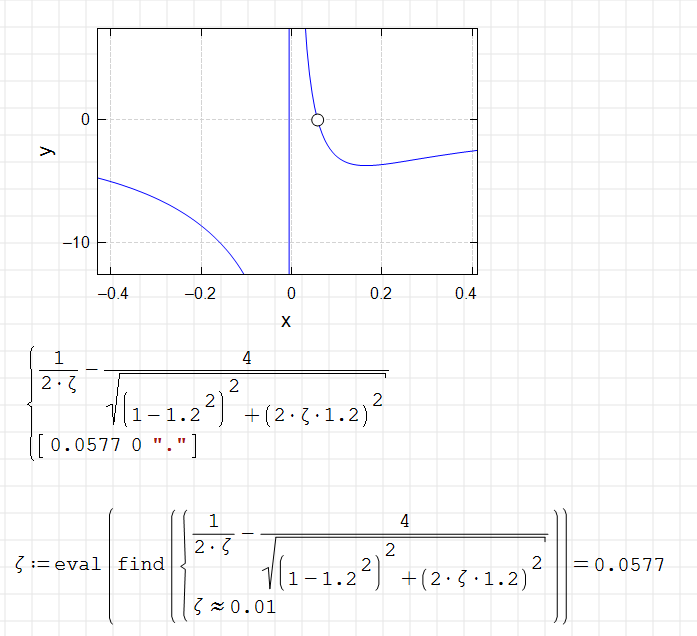
I think that the explanation by Gemini is not entirely correct. Yet, he hint on circularity is helpful.

If that was true, we would not have that circularity problem. Also we would not see the entire find command with it's arguments if we display the stored expression from the find block in the dynamic assistant.
Actually I believe that the find function (like any other function in any assignment does nothing (except for substituting existing definitions from the context) unless a result display is requested. I call this delayed evaluation.
Also, assignment to a variable should not affect anything above the current definition. Backfiring should be limited to absolute variables as sometimes used for iterations with on-the-fly animation.
If Gemini was right here, the simp() function in my above example would not help. simp() actually triggers evaluation because num2str() does so. BTW, in the given case S: eval(S) also does the job.




Plugin updated.
Changes:
- Draghilev solver added.
This is a very simple implementation.
MathcadToolbox-Draghilev-simple.sm (20.83 KiB) downloaded 634 time(s).
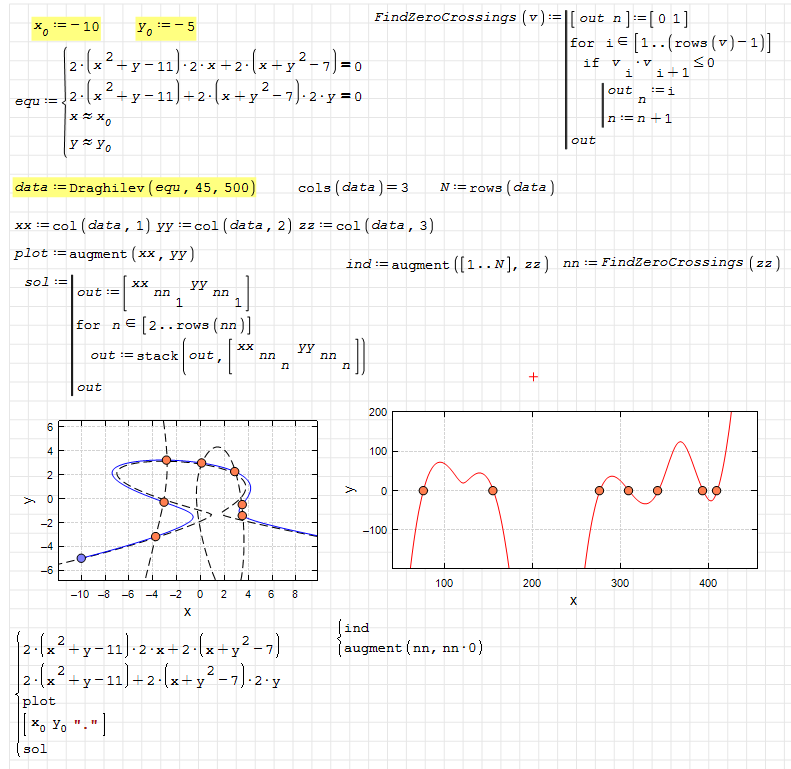
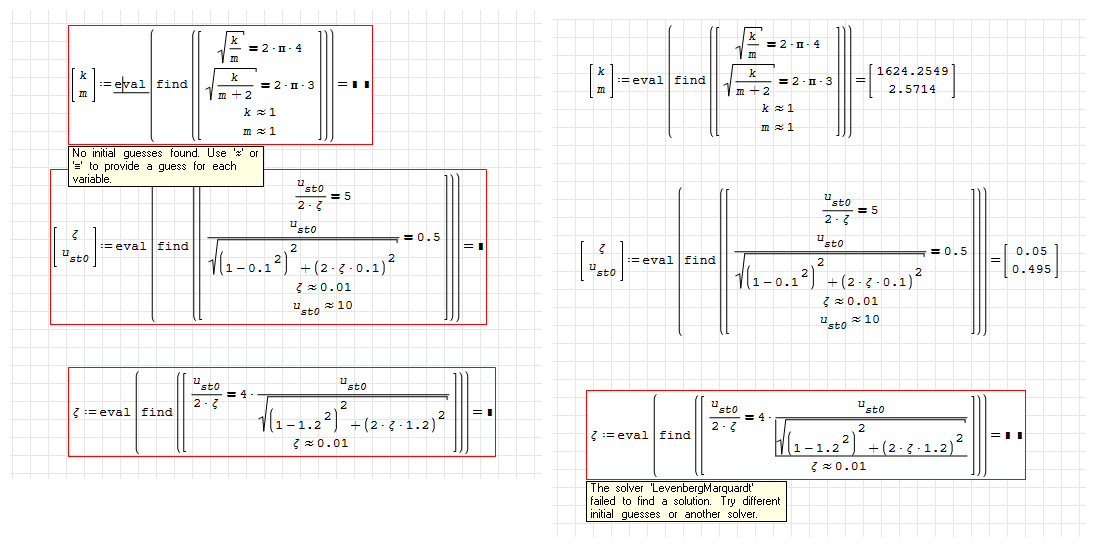
Wrote... The set of variables to be solved is now implicitly determined from all initial guesses (`≈`) provided in the input system. This removes the need to explicitly declare all variables. ...
Hi Viacheslav. Very good job! Instead of sending the equation with the user variables to the solver, and having problems with cyclic recursions, you can send a system of equations based on a single vector variable. This also enables the use of al_nleqsolve, which is the most robust solver available, and is also compatible with the solvers in the nonlinear solvers plugin. This is demonstrated in the code in the attached file, along with combining the x ≈ a notation with the x = a notation.
nsol-handling-equations.sm (56.51 KiB) downloaded 628 time(s).
Best regards.
Alvaro.
Wrote... Draghilev solver added.
Hi Viacheslav. With a matrix non-zero finder, like the one in Matlab, you can simplify the axis crossing detection.
MathcadToolbox-Draghilev-MFind.sm (30.45 KiB) downloaded 671 time(s).
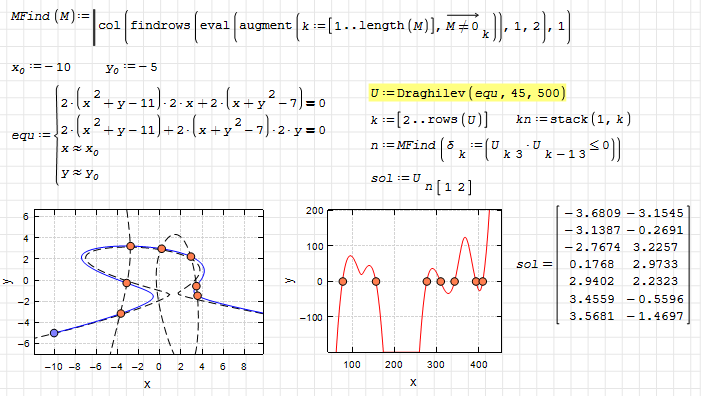
Best regards.
Alvaro.
QuoteThis is demonstrated in the code in the attached file, along with combining the x ≈ a notation with the x = a notation.
You might be interested to know that the find function was written using AI using the nsol function as an example. I have been working with AI for some time and now it can convert almost any description into code.
It understood perfectly what was happening in the nsol code, praised the author and offered the implementation as a find function. Of course, I told it what to do, but basically all the code was written by AI.
All numerical solvers that find() uses are also written by AI in 10 minutes.
The same goes for Draghilev's method, it is also based on your example. It is too complex to understand, but in general I know what is happening there, and for AI there were no difficulties at all.
Now I'm trying to port lsode (odesolve) from C code to c#. It's too huge to be done in one evening and there are many complexities, but the AI said that everything will be fine.
I will later connect all the existing numerical solvers to the find function, and all the numerical differential solvers to odesolve. In particular, it will learn to classify a problem by a set of equations and select an appropriate solver.
Unfortunately, when working with the AI, you need less time, but more knowledge. Not everything it offers corresponds to my level as a programmer.
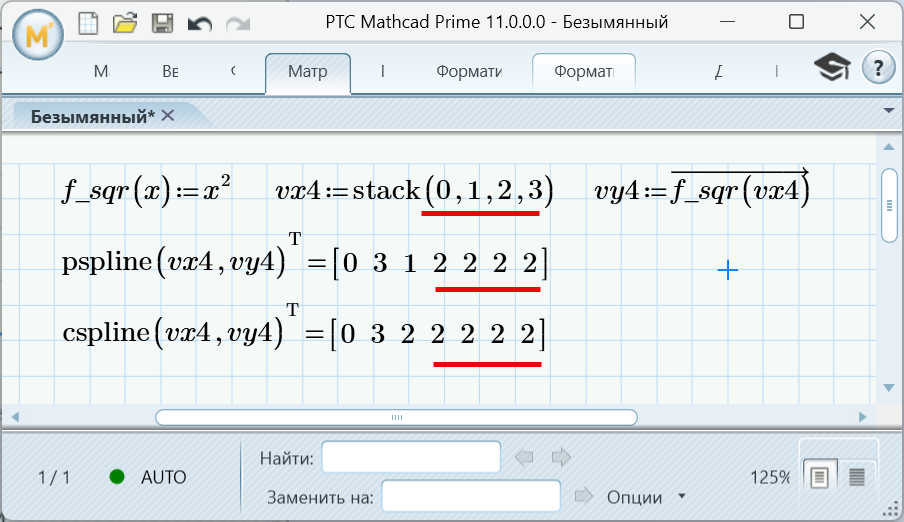
AI also helped to understand splines. It found an inaccuracy in the Mathcad.
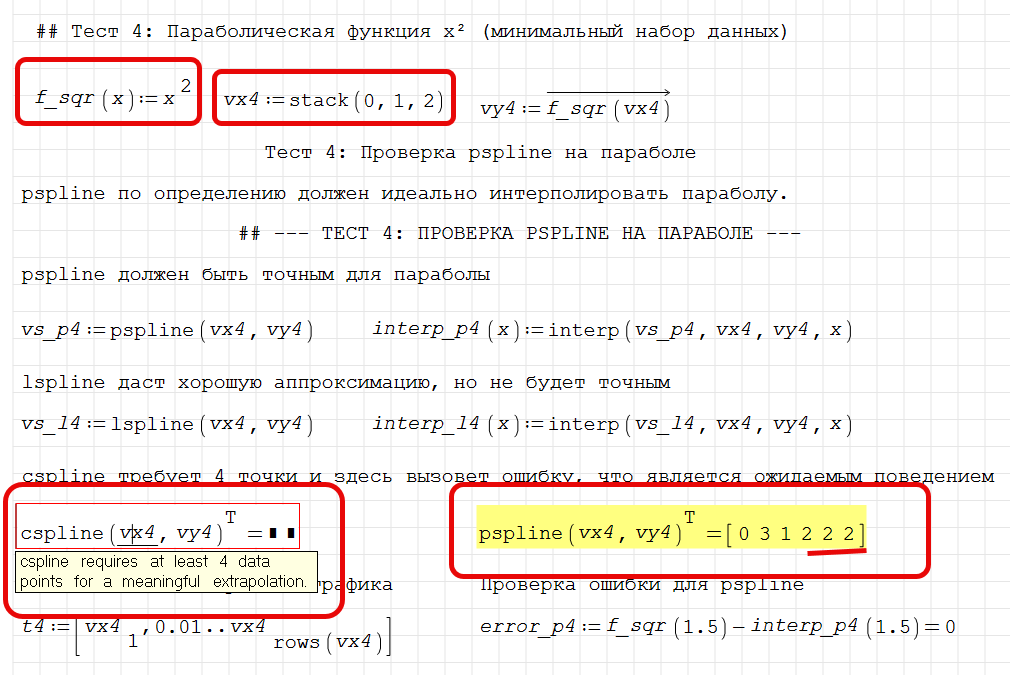
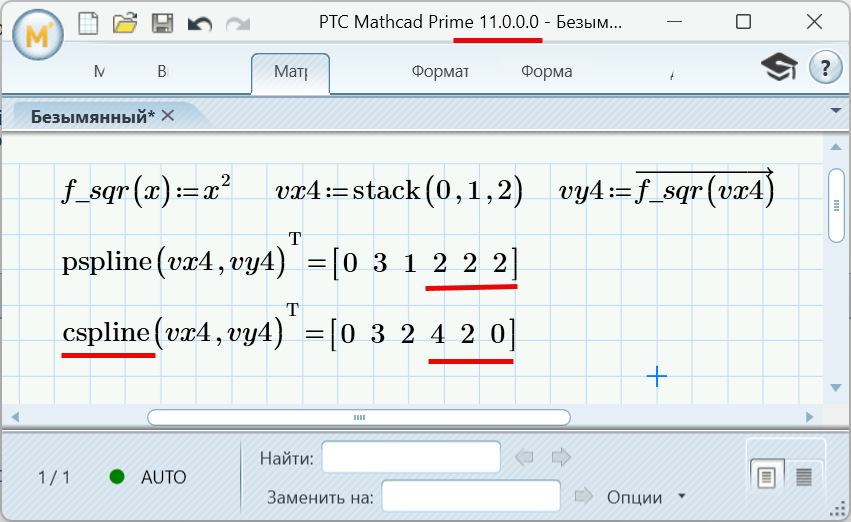
In that case, please also check ndsol , as the way it converts differential equations into systems allows for numerical solutions of hard coupled systems that I can only solve in SMath, but not Maple or Mathematica.Wrote... You might be interested to know that the find function was written using AI using the nsol function as an example. I have been working with AI for some time and now it can convert almost any description into code.
The nleqsol solver is the most powerful one you have at hand, it reminds me of the tksolver solver.Wrote... All numerical solvers that find() uses are also written by AI in 10 minutes.
Remember to add the option to have the Jacobian as an argument, and the ode solver too.Wrote... The same goes for Draghilev's method, it is also based on your example. It is too complex to understand, but in general I know what is happening there, and for AI there were no difficulties at all.
I haven't reviewed the code in the SMath plugin repository, but Adams' algorithm is clearly much faster than the others. Perhaps you could implement the way it evaluates D(t,u) values in rkfixed and RKadapt.Wrote... I will later connect all the existing numerical solvers to the find function, and all the numerical differential solvers to odesolve. In particular, it will learn to classify a problem by a set of equations and select an appropriate solver.
Wrote... AI also helped to understand splines. It found an inaccuracy in the Mathcad.
You can find the codes in SMath here: https://smath.com/en-US/forum/topic/sKU7o2/CSpline-interpolation#msg129361 . My idea for math software is that advanced functions should be written in their own code, with the exception of those that require a large number of flops (Matlab Word). This should make it easier for developers to discover bugs and optimize the core code. However, there is something very good about SMath's code for the cspline function. Unlike Mathcad, it doesn't require prior calculation of the matrix with splines, yet it still works very quickly.
Finally, as you refine your procedures and add examples, you'll eventually need to consider how to pass arguments to find and specialized ode solvers, as they won't be able to solve all problems with the default parameters. The option I suggest is something similar to the Options(~fname, "pname", pvalue) function you can find in nsol to store "pname" and "pvalue" as strings in the ~fname variable, and Options(~fname,"pname") to obtain pvalue. Remembering that in SMath, every function can modify the value of its arguments globally, and treating ~fname as if it were an object that has the pname parameters as if they were properties of an object.
Best regards.
Alvaro.

check-find.sm (37.51 KiB) downloaded 617 time(s).
Best regards.
Alvaro.
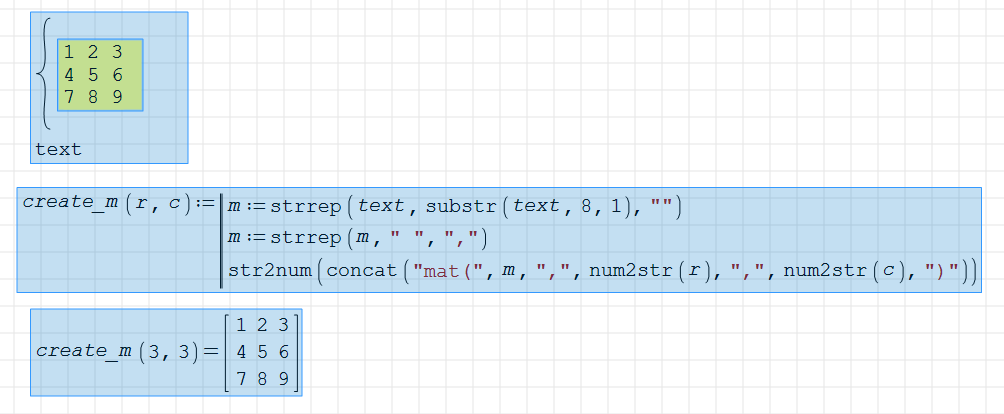
Problem is that it is easy to get the wrong sequence by slightly misplacing entries.
Also, it is not nice that the procedure can't guess the shape of the matrix from the arrangement of the entries.
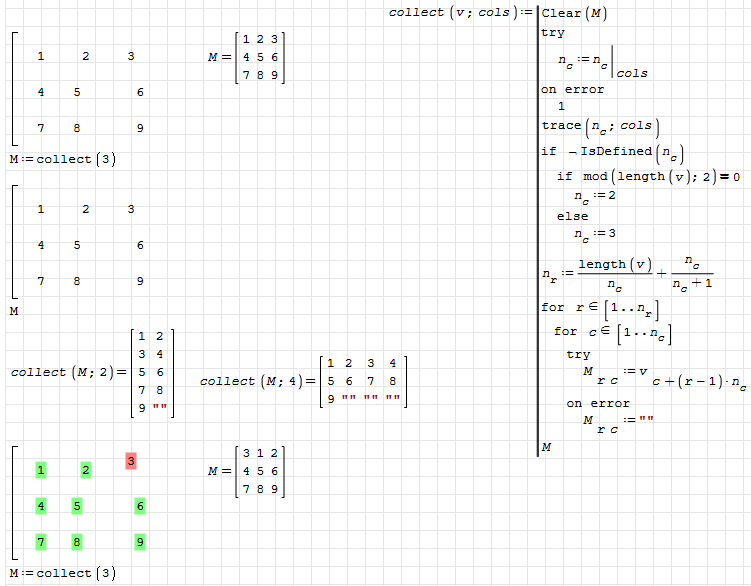
collect.sm (14.9 KiB) downloaded 594 time(s).
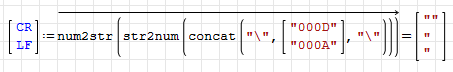
You can then handle text from both the mathcad block and description(), for example, using strrep(text,'CR,'LF)
Best regards.
Alvaro.
WroteSmath v1.3.0.9126, MathCad Toolbox v0.6.9367
These equations used to work in the original document, but today they all show red. Then I copy them and paste them to a new blank document, the 1st and 2nd equ works except 3rd one.
...
use Clear() function between 2nd and 3rd equations and evaluate:
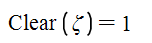
When this function is evaluated, the value of arguments in the function are cleaned.
Regards,
Oscar
WroteWroteSmath v1.3.0.9126, MathCad Toolbox v0.6.9367
These equations used to work in the original document, but today they all show red. Then I copy them and paste them to a new blank document, the 1st and 2nd equ works except 3rd one.
...
use Clear() function between 2nd and 3rd equations and evaluate:
When this function is evaluated, the value of arguments in the function are cleaned.
Regards,
Oscar
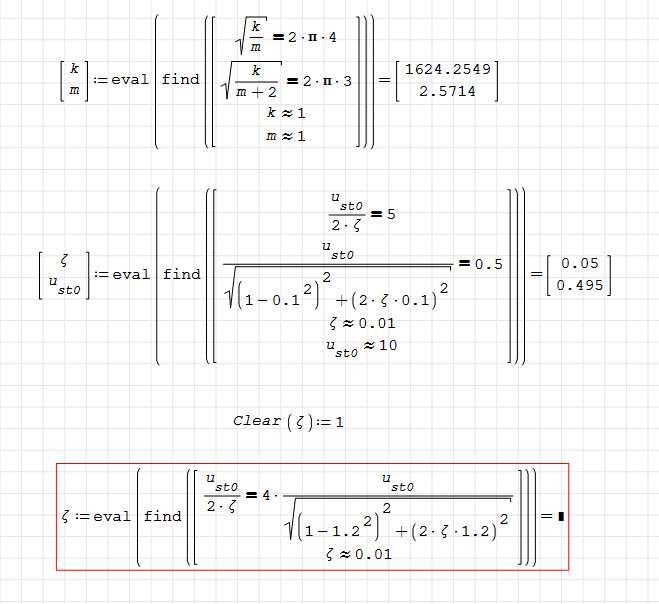
Wrote
Pay attention to this convention:
When you type ":" in SMath, you are assigneing a value to a variable and SMath renders as: ":=" .
When you type "=", you are asking for the value of a variable, or evaluating a function, and smath renders it as: "="
In your case, Clear() is a function, so, when you type "Clear(z[Ctrl+g]):1" which renders:
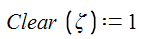
Here you must to type "1" and you are assigning the value "1" to "Clear(zeta)" . This is wrong.
The correct syntaxis to evaluate the function Clear() is : "Clear(z[Ctrl+g])=" which renders:
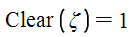
Here you don't type "1". The value "1" is an automatic response to evaluation of the function Clear(). It is the boolean answer of successfully having evaluated the Clear() function
Best,
Oscar
- New Posts
- No New Posts