NonlinearSolvers plugin - BDQRF, Bisection, Brent's, Broyden's, Newton-Raphson, Ridder's, Secant, Homotopy - Сообщения
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
I wish you all the best, and hope this time we will have more success than before.
Radovan
"splines" are not functions, just zombie interpolation.
You can't plug "zombie" in in a vector for ODEsolve or rk solve.
"simply deceiving because deceivingly simple"
Cheers, Jean
Forum Radovan Integral.sm (209,45 КиБ) скачан 879 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
I just wanted to point out that in spite of "zombies" which return numbers, we are sometimes forced to use root finding, optimization etc.
You also remind me to put some stress to the many examples you posted here regarding different splines including your comments about it. As you pointed out, splines being zombies or not - we often have to integrate, differentiate etc. using splines. I think there were some example of yours worth making plugin functions from them because, as we know, we often can not do that using the current spline functions inside SMath.
Regards,
Radovan
Smath splines [ainterp, cinterp, linterp] are "canvas" plotting
and on-line evaluation. They don't create a function thus can't be
use to integrate directly. You have two alternatives:
1. Dicretise/integrate finites differences
2. Transit via Infinitesimal modules
I went as far as I could in the attached. Plotting the components.
The "solve" block fails miserably, why?
It attempts to retrieve back to the integral that Smath does not
produce. The "solve" does not interpret the integral transit because
the solve block is a foreign entity. The Mathcad find(x) looks incorrect.
It depends upon initialisation. In this case the worng checks right.
Though the Mathcad Given/Find is often robust, it failed 1000's times
in my 15 years Mathacd collab.
Mathcad plots your integral, smath does not, thus it reflects in the "solve".
Please don't hesitate to correct me if I can help more.
Cheers, Jean
Forum Radovan Integral.sm (192,6 КиБ) скачан 990 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
WroteWhy is this working for me and not for you - I do not know.
Simple: the solve block of your version is more robust
or the chained code less reactive ? The other curiosity
5346 official release ..... 120 sec
5346 UNofficial release.... 14 sec
I got used to solve failure, rescue dichotomy.
BTW: eval(,) is not needed for f1(x)[faster].
Thanks Radovan, your collaboration is most appreciated.
Jean
Here is an unforunate example of FindRoot() being unable to solve a problems with units... While my very quick NR Line() solver works just fine.
I wonder if we run into max + number problem or devision by zero.
Hoping for a fix!
FindRootBug.sm (11,93 КиБ) скачан 864 раз(а).
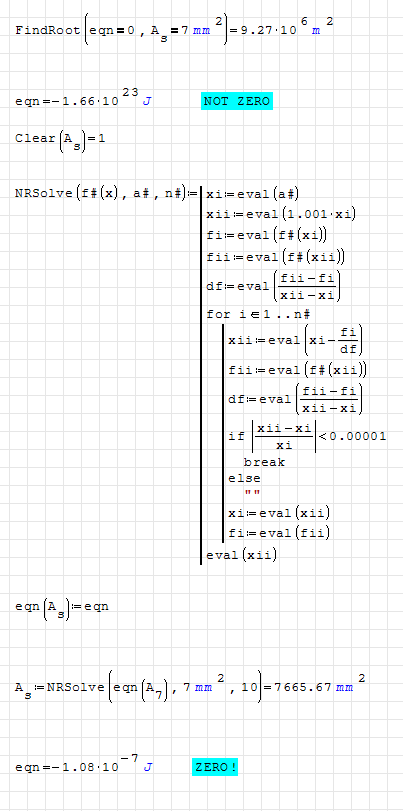
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
Initial conditions are chosen just on trial and error, and the calculation can diverge easily by slight changing of IC.
This is basically a second order polynomial having two solutions.
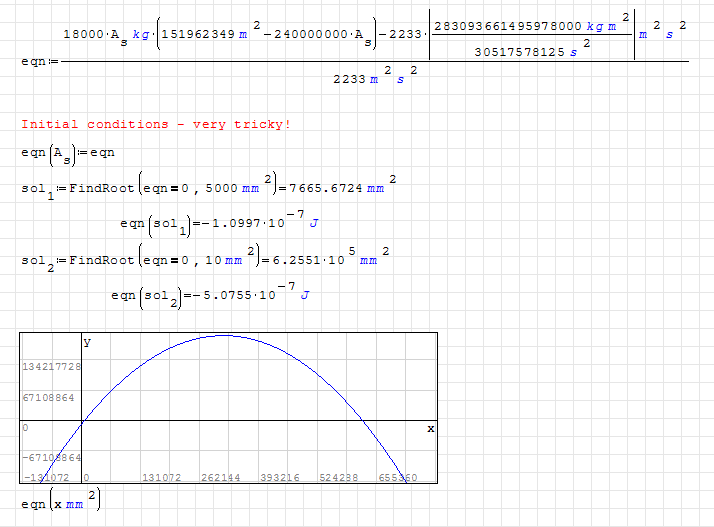
FindRootBug-corr.sm (16,62 КиБ) скачан 894 раз(а).
Regards,
Radovan
WroteActually, it could be done - but setting the initial conditions for FindRoot() could be very troublesome for this example.
Initial conditions are chosen just on trial and error, and the calculation can diverge easily by slight changing of IC.
This is basically a second order polynomial having two solutions.
Regards,
Radovan
Is there a reason why solver would gravitate to wards a solution further from initial guess? If it were just to follow the slope at the initial guess value it would arrive to the closer, and in my case correct, solution
So far in my expirience it is almost always possible to make FindRoot() solve by substituting just the right value. There has to be a reaon why the function tends to overshoot nearest solution by so much. Also when it does not find a desired solution, the number it spits out is not always a mathematical solution either
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
We might say that often some numerical procedures (especially nonlinear) may "go nuts" sometimes and give the unrealistic solutions. Therefore, we have to have the ability to use few of them for the same task. In this plugin there are many procedures for root finding we could use beside FindRoot(), but they are not working at the moment (or I do not know how to use them anymore).
Regards,
Radovan
For single variable problems I plan to add these algorithms, in which solutions are bounded in a range. Even, I guess would be possible to add some kind of "filter" to discard some solution (however, would be a replacement for something that should be done in any case: sanity check if the result fits personal needs).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
This is exactly I was talking about - many different methods for the same task.
It would be very encouraging (less frustrating I hope) to have all those methods at our disposal as functions incorporated in plugins .
Best Regards,
Radovan
Yes Radovan: a "Peak/Deep/Root" in the menu would be great,
c/w different options. As robust they will look at the design
stage, they will not be so. Read again "ULP".
Going back to "FindRoot": as it looks in similar applications,
it is same or so Mathcad, a very universal code. For the free
finding solutions, IC must be either 0 or 1 [1 to releive from
"divide by zero"]. In examples [1,2] notice the switch of the
solutions. Be careful as it may scrap the project !
Examples [2, 3], Quaternion and Frobenius are robust and correct.
I didn't completely understand Alex example/problem. A case of
constrained IC difficult to handle and prone to fail.
Cheers, Jean
Solve Given_Find [UN test Robutness].sm (31,18 КиБ) скачан 825 раз(а).
Solve NON-Iterative SIG.sm (44,25 КиБ) скачан 911 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
Regards,
Radovan
=>...For the free finding solutions, IC must be either 0 or 1
[1 to releive from "divide by zero"]<= ... {previous message}
Maybe you are not up to date vs Davide ?
Jean
- Новые сообщения
- Нет новых сообщений


![2016-10-27 09_19_33-SMath Studio - [FindRootBug.sm_].png](/ru-RU/files/Download/YsmTTL/2016-10-27-09_19_33-SMath-Studio---[FindRootBug.sm_].png)

![2016-10-29 17_26_47-SMath Studio - [fenov.sm_].png](/ru-RU/files/Download/SdnnEk/2016-10-29-17_26_47-SMath-Studio---[fenov.sm_].png)