NonlinearSolvers plugin - BDQRF, Bisection, Brent's, Broyden's, Newton-Raphson, Ridder's, Secant, Homotopy - Сообщения
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
WroteThat's not a bug Radovan:
=>...For the free finding solutions, IC must be either 0 or 1
[1 to releive from "divide by zero"]<= ... {previous message}
Maybe you are not up to date vs Davide ?
Jean
I was using SMath 0.98.6128 an NonlinerSolver 1.1.6099.14159
Regards,
Ra
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
WroteThank you guys, these examples are very useful to fix the bugs in this plugin
I'm working to a new version of the code, almost totally refactored.
Looking at your examples seems there are several things to fix in my preprocessor; with some tweak, it is able to solve it.
now I just have to find some consistant way to make it working always
Davide, any progress about this plugin and its new version?
Regards,
Radovan
WroteDavide, any progress about this plugin and its new version?
Regards,
Radovan
Hello Radovan!
More or less, I'm trying to make it working on the numerical functions (those containing if/else, etc...), requires some more refactoring, I'll see if I can focus on this plugin in the coming weeks...
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
WroteMaybe, I don't understand much in there ?
Jean
Page1 Unknown Solve.sm (30,3 КиБ) скачан 963 раз(а).
Helo Jean,
You should define f(x) not f(u). See the file, please. Was that your question?
Page1%20Unknown%20Solve-2-corr.sm (34,64 КиБ) скачан 1105 раз(а).
Regards,
Radovan
Example in context works fine for me. Integrator is now "scalar" 6179.
It enables the Fourier Quantum double integral, though awfully slow.
For N =31, CoC takes > 2hrs [Win 7 1.6 GHz]. ∫(x) comes from Maple.
Jean
Integral Curve Nuance.sm (26 КиБ) скачан 911 раз(а).
I wrote a formula (biaxial bending in a column) to calculate unknown input loads based on known response. A key to practical use of the formula is to solve for unknown response based on known input loads (backwards of what formula does). When using findroot() for this purpose i run into error:
FidRoot-CustomFormulaSolution.sm (537,63 КиБ) скачан 927 раз(а).

What am i doing wrong?
Thanks!
- Just evaluate: displays result vector and executes embedded assignment
- Assign and evaluate in the same region: Error (symbolic evaluation reveals that the expression isn't executed but just stored as if it was inside line())
- Assign and evaluate in separate regions: displays result vector and executes embedded assignment upon display.
- Assign wrapped in eval() and evaluate in the same region: displays result vector and executes embedded assignment (here, eval() seems to be a friend of FindRoot())
In the sheet below I tried to demonstrate how to solve a system of equations using FindRoot() as alternative to Solve(). However, I am not sure how to explain the behaviour to the students. Should we generally avoid assignment with integrated evaluation for the time being?
![2018-12-12 00_06_28-SMath Studio - [Kerbformzahl Lochstab Biegung FKM.sm_].png](/ru-RU/files/Download/NhPn5e/2018-12-12-00_06_28-SMath-Studio---[Kerbformzahl-Lochstab-Biegung-FKM.sm_].png)
Kerbformzahl Lochstab Biegung FKM.sm (700,43 КиБ) скачан 881 раз(а).
WroteShould we generally avoid assignment with integrated evaluation for the time being?
Yes, they should be avoided. There are several known issues while using implicit assignments, I plan to remove them when I'll have the possibility to commit a major update to this plugin.
Moreover now SMath Studio supports multiple assignments by matrices on LHS, therefore it shouldn't be a big loss.
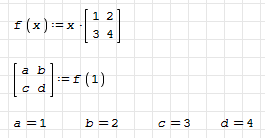
WroteWroteShould we generally avoid assignment with integrated evaluation for the time being?
Yes, they should be avoided. There are several known issues while using implicit assignments, I plan to remove them when I'll have the possibility to commit a major update to this plugin.
Moreover now SMath Studio supports multiple assignments by matrices on LHS, therefore it shouldn't be a big loss.
Perhaps I wasn't clear enough. My example doesn't show any problem with embedded/implicit assignment (at least nothing obvious). What I mean is if you write an assignment with := and in the same region ask for display by = . This one seems to be a problem. Maybe, the two features are related, I don't know.
If you drop integrated/implicit assignment, perhaps would be a good idea to return a set of boolean equations which can be used with at(), just like with Solve(). Then you can easily operate with multiple solutions without having to clear inbetween.
WroteBe my guest if you want to solve it
A similar problem problem kept the Mathsoft Collaboratory [mostly Jean]
busy for a while, solving for 22 variables. That was possible finally
from Given/Find with infinitely many trial/error constraints.
Given/Find Mathcad 8 Pro solves for 250
Given/Find Mathcad 11 solves for 400 but not of that nature
Given/Find MCD 11 solves for 399 in for loop as the next call
benefits of the previous estimates. That was done solving a DE
of variable coefficients as functions [something like Frobenius]
The Mathsoft 22 variables surely does not exist anymore in my old box
as it was "secret" about what is was. Maybe the Originator said 'thaks'
but not sure as commonly Done-Gone !
Yet, I don't completely understand the problem and its generation.
Cheers Radovan ... Jean
WroteBe my guest if you want to solve it
Assuredly not a profitable guest !
I don't understand much in there.
Primer38-doomed.sm (39,31 КиБ) скачан 886 раз(а).
Primer38-doomed_1.sm (44,63 КиБ) скачан 847 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
WroteWroteBe my guest if you want to solve it
Assuredly not a profitable guest !
I don't understand much in there.
Primer38-doomed.sm (39,31 КиБ) скачан 886 раз(а).
Primer38-doomed_1.sm (44,63 КиБ) скачан 847 раз(а).
Thank you Jeaan for your efforts, but I think we do not understand each other. This is not a fitting problem but finding roots of nonlinear system of equations
The solution was found in Mathcad - this post - and some other software but never in SMath
Regards,
Radovan
Wrote
Here is the same problem solved in Mathcad
Regards,
Radovan
Hi. Can you show the guess values for x and y? And k before Find too. I get a very different k value. Remember that for numerical procedures, guess values are part of the solution, not of the problem.
Thanks in advance.
Best regards.
Alvaro.
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
WroteWrote
Here is the same problem solved in Mathcad
Regards,
Radovan
Hi. Can you show the guess values for x and y? And k before Find too. I get a very different k value. Remember that for numerical procedures, guess values are part of the solution, not of the problem.
Thanks in advance.
Best regards.
Alvaro.
Thank you Alvaro for your interest in these problems. Here is the file once more.
Primer38-doomed1.sm (31,96 КиБ) скачан 875 раз(а).
This is a system of nonlinear algebraic equations. If one takes a look at the calculation here it is obvious that any gradient algorithm for solving this system will fail. Therefore, some non-gradient method might solve this (direct solving or some minimization procedure). There are some functions in the NonlinearSolvers plugin, but unfortunately, there is no update of them for a long time and many of them do not work anymore. All of these years I mentioned that we need here some well tested and robust library incorporated in SMath regarding these problems. There are no other plugins which will address these problems (AFAIK) and I am not sure that will ever be any.
Regards,
Radovan
WroteThis is a system of nonlinear algebraic equations. If one takes a look at the calculation here it is obvious that any gradient algorithm for solving this system will fail. Therefore, some non-gradient method might solve this (direct solving or some minimization procedure). There are some functions in the NonlinearSolvers plugin, but unfortunately, there is no update of them for a long time and many of them do not work anymore. All of these years I mentioned that we need here some well tested and robust library incorporated in SMath regarding these problems. There are no other plugins which will address these problems (AFAIK) and I am not sure that will ever be any.
1. You seem not happy of the result by plugging [x, y] from the other software.
Did you enter enough decimals ? or that software is short of more ?
2. The Smath FindRoots is not robust in there but it can reproduce results
from your source software with more decimals that you collected.
3. Presumably the software is Matlab ?
4. In short: for a fixed Phi, you are attempting to solve pairwise [x,y]
as you scan over 'z'. Isn't true that any pairwise [x,y] will find a valid
solution or closely ? Stated otherwise: the unique non trivial pair [x,y]
is extremely sensitive to initials. That reminds me the Mathcad rootScanner
that I designed for some extremely sensitive initials. But that one tool
is only for one variable.
Cheers Radovan ... Jean
Primer38-doomed1[Solve paiWise].sm (10,31 КиБ) скачан 782 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
WroteHello Jean,
The solution is from Mathcad (Given/Find)
With an increased number of decimals.
That was my guess, no shame borrowing the hammer as needed.
γRK(T,x):=eval(program) ... > 4 times faster.
Cheers Radovan ... Jean
- Новые сообщения
- Нет новых сообщений

![2016-10-24 18_27_07-SMath Studio - [FindRoot.sm_].png](/ru-RU/files/Download/WAgdXS/2016-10-24-18_27_07-SMath-Studio---[FindRoot.sm_].png)