Thank you, I have a refactored version running on my system where the el(#) issue doesn't happens, thus I haven't noticed it. I'll look in these days if I can fix it even in the current code. I'll add Taylor(4) in the refactored plugin (and I'll see if I can improve or I have to remove Taylor(3), that wasn't designed for multi-variables functions).

Hello Davide,

I am attempting to use FindRoot() function for a rather unorthodox purpose: to arrive to an iterative solution of an excel spreadsheet (if you think this is nuts you can stop reading right here).

Idea is:
1. substitute value in excel
2. get value from excel
3. if value obtained is not zero go back to "1"

I wrote a simple Newton-Raphson for() loop that works, however I am puzzled why FindRoot() or NewtonRaphson() cannot achieve similar purpose.

See PDF attached.

Файл не найден.Файл не найден.Файл не найден.

P.S.: after two minutes of "pause&think" I have realized that there is a good chance that FindRoot(), when iterating, cannot execute a call to another plugin's function, is this correct?

P.P.S.: I found the reason - it is likely the excel_IO function itself. More weekend work for me to do.

Hello Alex,

Wrote

P.P.S.: I found the reason - it is likely the excel_IO function itself. More weekend work for me to do.

Yes, at first glance I think the issues is that EXCEL_IO returns a value even you you feed it with an unknown, hence while FindRoot() preprocess the function gets a result -> no unknowns; since now NS' nightly is better structured I think in future I might provide some workaround even for these cases.

Wrote

Hello Alex,

Wrote

P.P.S.: I found the reason - it is likely the excel_IO function itself. More weekend work for me to do.

Yes, at first glance I think the issues is that EXCEL_IO returns a value even you you feed it with an unknown, hence while FindRoot() preprocess the function gets a result -> no unknowns; since now NS' nightly is better structured I think in future I might provide some workaround even for these cases.

Thank you Davide,

I do have to fix excel plugin no matter what though. Right now it converts any variables passed to it to string (string of a variable name if undefined) and than to number - this is likely a part of the problem.

P.S.: after two minutes of "pause&think" I have realized that there is a good chance that FindRoot(), when iterating, cannot execute a call to another plugin's function, is this correct?

That makes sense. You may have to pull-out the data from XLS,
reconstruct in Smath and spool back in XLS. Can't you do
directly in XLS via "Target value". They claimed the special
"Target solver" could solve 400 variables

As anyone could see, there were lots of posts here for this plugin.

After so many years struggling with SMath and nonlinear problems (system of nonlinear algebraic equations, nonlinear optimization) I have to admit that whenever I want to do that in SMath (more than two, three variables), I get few gray hairs . See for example this one (doomed for me...). At the moment, I just do not know how to solve this



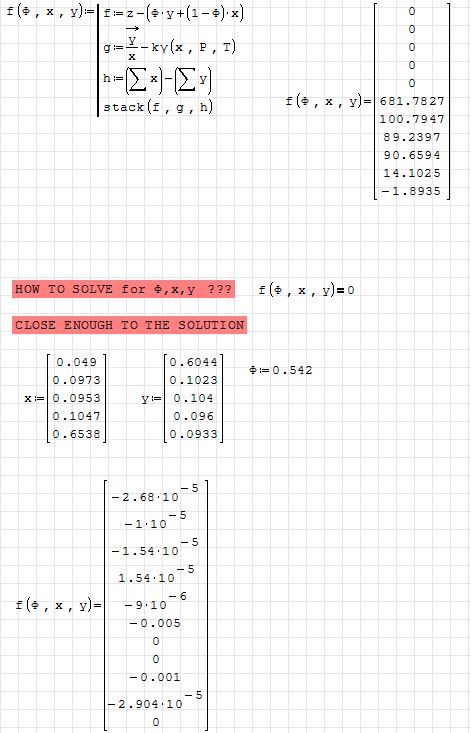
SMath file - Be my guest if you want to solve it

Primer38-doomed.sm (27 КиБ) скачан 90 раз(а).

Regards,
Radovan

Wrote

I just do not know how to solve this

f(,x,y) does not generate a function, just a vector.
So, there is nothing to solve directly. If that vector is
a vector of initial guesses, you must have 11 relationships
wrt each of the 3 parameters. From there, the recursive
"Divide and Conquer" algorithm sould solve. This is the Mathcad
"Given/Find", has been working for up to 22 equalities,
not too easy to initialise.. The near 0 all 11 elements look
pure coincidence. I guess I'm missing something.
In the "Solve Inverse Recursive" just plug your new 'k'
from your work sheet.

Can't help much !!!

Smath "FindRoots" is a "Divide and Conquer" solver.

Thank you Jean for the reply,

The problem is of 11 equations-relationships with 11 unknowns. The function f() has three arguments (phi - single value, x,y - vectors with five elements each) returning 11 element vector.

We have to find phi,x,y where all the elements of f() will be close to zero. Moreover, if we talk about the acceptable range of phi,x,y - phi is in the range [0,1], x,y are positive values with the conditions sum(x)=1, sum(y)=1. Anyway, this is a quite standard calculation in chemical thermodynamics - vapor, liquid equilibrium.

From my experience, I just wanted to note (once more) that solving similar problems - like this one - might be quite a frustrating thing in SMath.

Here is the same problem solved in Mathcad



Regards,
Radovan

Oh ! YES : liquid/vapor equilibrium.

The Mathcad Given/Find code is much different and much more convivial
than Smath 'FindRoot'. The 5 examples output same results with a bit
of attention wrt the vector 'initial': FindRoot' much less robust.
The Mathcad Given/Find solves first [internally] symbolic, which
FindRoot does not.

I didn't completely understand your vector construction.

The final solution of the Frobenius DE variable coefficients
goes via Given/Find. I will work that long monkey business example,
hoping Smath doing it.

Jean

Solve Given_Find [UN Cylinder].sm (62 КиБ) скачан 81 раз(а).

Frobenius => no sweat !

Jean

Solve Given_Find [UN Frobenius].sm (37 КиБ) скачан 108 раз(а).

... (suite)
In the above Frobenius, in the F vector,
it only necessary to equate C1=1
the remaining elements need not be equated to 0

Wrote

I didn't completely understand your vector construction.

That's one of my main points I mentioned many times. Actually, one do not have to understand the vector construction of the equations. It is important that the function returns the numerical vector of the same length as the length of the variable numbers. Solvers which uses Jacobin analytically are sometimes totally useless. Only the methods which are gradient free (or numerical Jacobian) might help here. Davide included in FindRoot() many algorithms for nonlinear solvers (working in background).

Wrote

The final solution of the Frobenius DE variable coefficients
goes via Given/Find. I will work that long monkey business example,
hoping Smath doing it.

Nice, FindRoot() will do the job here for the Quternion system if the init vector elements *p,q,r* have different initial values (not zero values i.e.)

Regards,
Radovan

Wrote

Frobenius => no sweat !

Jean

Solve Given_Find [UN Frobenius].sm (37 КиБ) скачан 108 раз(а).

Thank you for this example,

FindRoot() goes with it well. You have nine clear defined expressions (F vector) with nine unknowns (V vector), and FindRoot() will do the job

By the way, if all the initial values are the same we can use the standard trick : V[9:=0 , V:=V+1 : and all nine vector elements will have unity values. This is all right, I think, because this will give: Unknowns(F)=[C] which means the unknowns is C - it happened to be a vector. But, your construction is more understandable, I think.

Moreover, this way will also work



Regards,
Radovan

Thanks Radovan,

Your collaboration is most appreciated. I agree with you:
"solving" in generally a painful task, more painful in Smath
than in Mathcad. The set of Frobenius coefficients C1 works well.
The set C2 does not solve ... the same pattern as C1.
FindRoot => not robust for Frobenius C2
I can't see any possible repair /

Jean

Solve Given_Find [UN Frobenius C2].sm (23 КиБ) скачан 68 раз(а).

You are welcome Jean,

Your last two examples, basically, represented system of linear equations, and FindRoot() should not have to much problems in solving them.

In this example, you missed one equation: C[3:=1 (there were 8) and there were 9 variables. Mathcad could cope with this.

Here is the corrected version.

SolveGiven_Find[UNFrobeniusC2]_corr.sm (21 КиБ) скачан 78 раз(а).

Regards,
Radovan

Thanks Radovan,

I tried the 9 components 'F' before posting. The error was not there.
The bug was that once the solve had failed, it wouldn't rescue itself.
The trick was to delete the red "FindRoot" and recall from the menu.
This bug is one of those "Shadow in the context".

Cheers, Jean

Hello,

Here is the test example which is intended to point out that SMath should be capable of solving this (two nonlinear equations with two unknowns), by using the functions from this plugin.



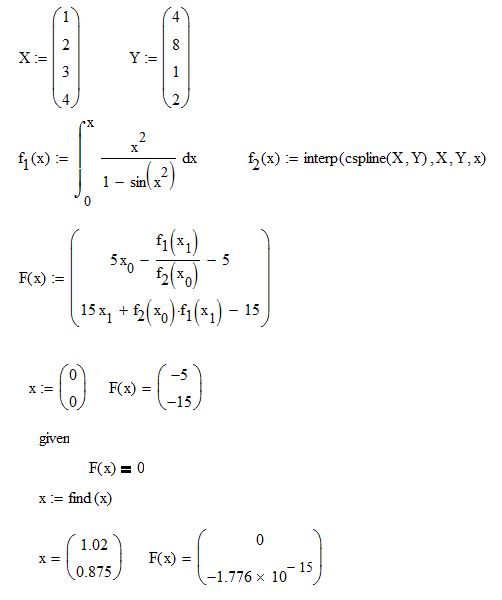
I failed by everything I try.

Regards,
Radovan

Here is another "cup of tea" to help you grow white hairs.

Thanks for your attached challenge.
Andrey, Martin, Davide ...: where are you in there ?

Cheers Radovan, Jean

ODE Rkadapt Minerr.sm (48 КиБ) скачан 71 раз(а).

Hello Jean,

I tried to solve those optimization problems few years ago (see this for example) by myself and with the help of Davide's NonlinearSolvers plugin (dozen of functions are there). You can find many examples during the plugin functions testing. Unfortunately, many of these files on this thread do not work anymore due to the time gap, lack of enough users for testing, my own ability shortcomings for testing them, and changes in SMath itself. Some of them might work with slight changes (only part of them though). On the other hand, some examples were terribly slow.

Your example (uncompleted - missing the optimization of initial conditions) might get solved completely in SMath but we need the Davide to check the plugins function and let us know how to use them. Therefore, we have to be patient a bit.

Best Regards,
Radovan

Thank you guys, these examples are very useful to fix the bugs in this plugin

I'm working to a new version of the code, almost totally refactored.
Looking at your examples seems there are several things to fix in my preprocessor; with some tweak, it is able to solve it.



now I just have to find some consistant way to make it working always